基于K-means聚类算法的任务定价

朱家明，曹绮琦，潘雪航，钱礼会，李春忠

(1.安徽财经大学统计与应用数学学院，安徽 蚌埠 233030；2.安徽财经大学财政与公共管理学院，安徽 蚌埠 233030)

根据中国互联网络信息中心发布的第41次《中国互联网络发展状况统计报告》显示，截至2017年12月，我国网民规模达7.72亿，普及率达55.8%[1]。随着时代进步，越来越多的企业开始通过互联网寻求外部资源，一种新的非常有创意的发展模式正悄然兴起，即众包。“众包”一词于2006年首次提出，指一个公司或机构把过去由员工执行的工作任务以自由自愿的形式外包给非特定的(而且通常是大型的)大众网络的做法[2]。而对于众包任务的定价问题，不同的学者有不同策略。徐芹[3]在垄断型市场下研究相应平台对双边用户的定价策略，但相关影响因素的考虑不够全面；孙信昕[4]则认为应该根据每个工作者提交的成本、希望的任务数量以及完成质量对任务进行定价，但其模型适用范围小，仅适用于任务质量易测量的简单任务。为此，本文采用K-means聚类算法定量分析域内会员数量、任务点距离、任务定价与任务完成情况之间的相关性，并为任务进行合理定价。

1 数据的获取及假设

数据来源于2017年全国大学生数学建模竞赛B题。为便于解决问题，提出以下研究条件：(1)用户选择任务只与任务价格和自己与任务地点的距离有关，没有其他因素的影响；(2)用户选择任务会权衡任务价值和自己完成任务的成本，如果成本高于价值，则用户不会选择该任务；(3)APP中的任务定价在用户预订前就已确定，与任务周围会员的数量和会员距离的远近无关；(4)未完成任务的地理位置只考虑广州市和深圳市(因为这两个城市未完成任务数量比重最大)，而不考虑其他城市；(5)任务打包发布时，会员接单会完成所接的所有任务。

2 任务定价影响因素的相关性分析

2.1 研究思路

任务定价在执行之前，故任务的定价决定执行情况，执行情况对定价无影响。根据已知数据，可对任务的位置进行聚类分析，从任务与中心点间的距离及任务的位置等任务定价影响因素探究定价规律，然后根据计算得出各任务区中的会员数量，与各任务区中的价格进行比较，分析定价规律[5]。

2.2 研究方法：K-means均值聚类[6]

若将n个样品分成k类，则先选择所有样品中距离最远的两个样品xi1、xi2为聚点，使得

d(xi1,xj2)=di1j2=max{dij}。

(1)

然后选择第3个聚点xi3，使得xi3与前两个聚点的距离最小者等于所有其余的与xi1、xi2的较小距离中最大的，即

min{d(xi3,xir),r=1,2}=max{min{d(xj,xir),r=1,2},j≠i1,i2}。

(2)

最后按相同的原则选取xik，重复前面的步骤，直至确定k个聚点xi1,xi2,…,xik。

k-means均值聚类的步骤(样品之间的距离采用欧氏距离)如下：

设第k个初始聚点的集合是

(3)

记

(4)

于是，将样品分成不相交的k类，得到一个初始分类

(5)

从初始类G(0)开始计算新的聚点集合L(1)，计算

(6)

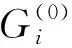
(7)

从L(1)开始再进行分类，记

(8)

得到一个新的类

(9)

重复上述步骤m次，得

(10)

(11)

与

(12)

相同，则结束计算。

变量x与变量y间的相关系数

(13)

2.3 研究结果

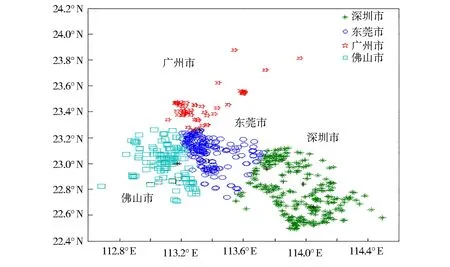
图1 任务结束地区位置聚类图Fig. 1 Map of completed task location cluster

运用MATLAB软件编程，得到已结束任务经度纬度的位置聚类图如图1。

为了研究任务点位置对定价的影响，利用已结束任务位置聚成4类的结果，运用EXCEL筛选，分别计算佛山市、深圳市、广州市和东莞市任务定价的均值及其区域内会员数量。结果见表1。

以4个聚类中心的位置作为定点，分别计算4个区各任务点到其中心的距离(单位：m)，分析任务价格与任务距离之间的相关关系，结果见表1。

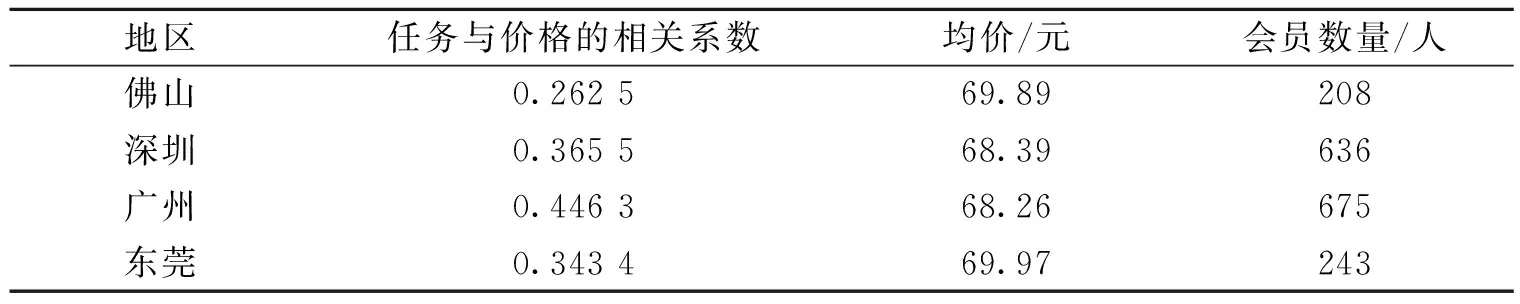
表1 各地区任务价格和距离的相关系数、任务均价和会员数量Tab. 1 Correlation coefficient of task price and distance,mean task price and number of members by region

从表1可以看出各地区的任务价格和任务距离存在一定的相关关系，并且是正的相关关系。也就是说各任务的定价和距离有关，任务点到聚类中心的距离越大，则任务的定价越高。

由表1求出各地区任务定价的均值与会员数量间的相关系数为-0.995 7，表明这两者显著相关，且地区的会员数量越多，其任务定价越低。

3 基于最小二乘法对未完成任务进行重新定价

3.1 未完成任务的原因分析

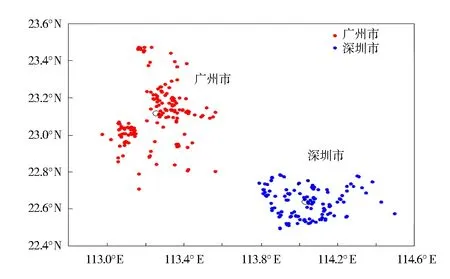
图2 未完成任务位置聚类图Fig. 2 Location clustering of unfinished tasks

3.1.1 研究思路

对于任务未完成的原因，可以先利用MATLAB对未完成任务位置进行可视化处理，得出位置的分布特征，再进一步分析造成这种分布可能的原因，然后可以从区域内会员数量和任务价格等方面探究这些因素是否会影响任务完成情况[7-9]。

3.1.2 研究结果

根据散点图可知未完成情况有明显聚集现象，运用MATLAB绘出了未完成任务位置的聚类图，结果如图2所示。

图2中聚类中心的位置坐标分别是(22.64°N，114.03°E)和(23.12°N，113.25°E)，在地图上确定分别是深圳市龙华区和广州市越秀区。由于这两个地区内会员数量较大，经济也发达，所以不存在会员不够而任务过多的情况。综合考虑各种影响因素，认为价格的高低直接影响任务完成情况，并且价格越高，任务完成情况越好，反之，则越差。为此，利用EXCEL软件，计算每个价格的任务完成率。

在统计学中，样本数量在30以下的是小样本， 30以上的是大样本。小样本由于样本数量过少，不具有代表性，所以剔除了个别小样本数据，保留任务完成数在30以上的样本。各价格下任务完成情况的统计结果如表2所示。

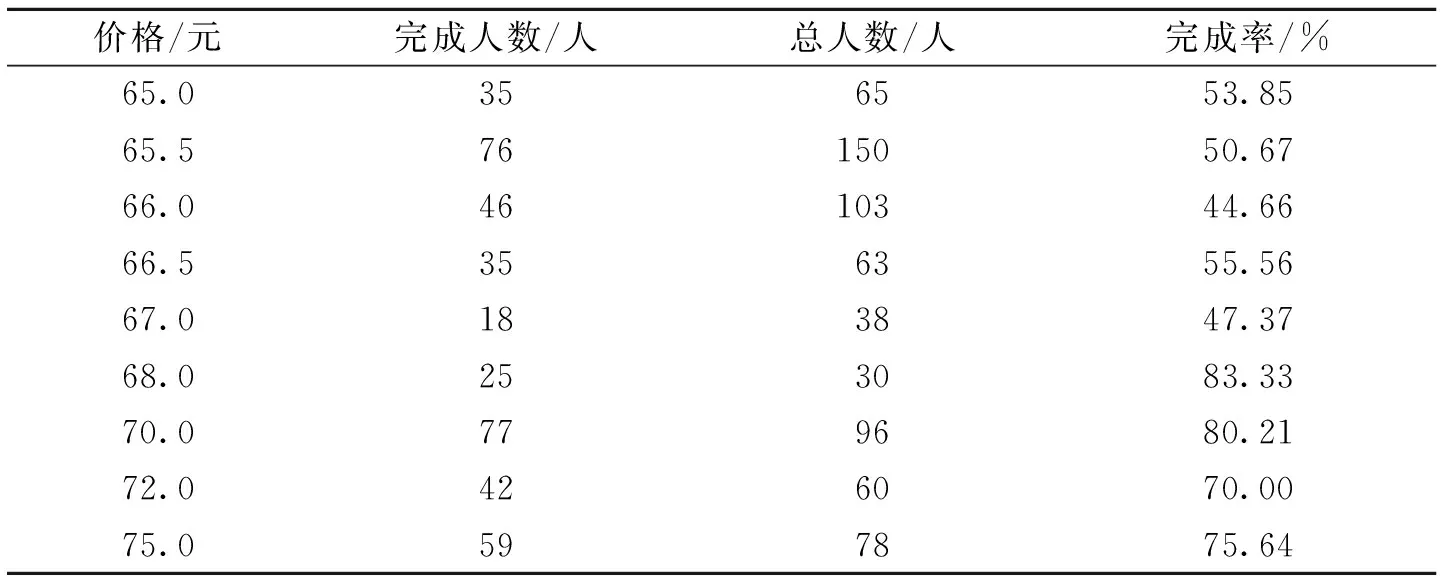
表2 各价格下任务完成情况Tab.2 Tasks completed by price

价格和完成率的相关系数高达0.683，存在明显的正相关关系，拟合方程为y=-0.027x5+9.611x4-1 356x3+95 713x2-3×106x+7×107。拟合曲线见图3。

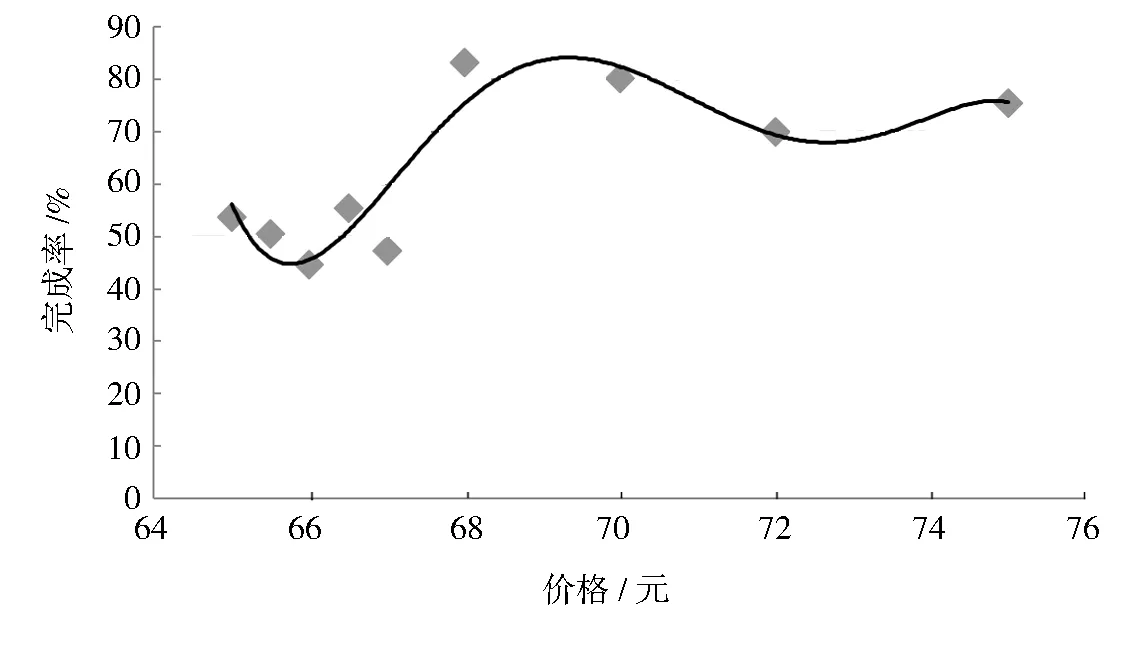
图3 各价格下任务完成情况的拟合曲线Fig. 3 Curve of tasks completed by price

图3中的曲线拟合的可决系数为0.8544，表明拟合程度较高。由点的分布规律可知定价低的任务完成情况明显比定价高的任务完成情况差，所以价格的高低能直接影响任务的完成情况。而任务的定价和完成率不存在明显的线性关系，可能是因为完成任务的难易程度不一样，包括交通的便利性、完成成本等方面因素，难度大的任务，定价再高也必然存在不能完成的现象。

3.2 未完成任务的重新定价

3.2.1 研究思路

首先，对已知任务的完成情况进行筛选，得出已完成任务与未完成任务各自的分布情况；然后对价格进行排序，得到已完成任务与未完成任务的价格走向，已完成任务的价格曲线即为任务定价模型；最后由模型计算出未完成任务的新价格，再与原方案的未完成任务的价格进行比较得出结论。

3.2.2 研究方法——最小二乘法

由给定的一组测定的离散数据(xi,yi)(i=1,2,…,N)，求自变量x和因变量y的近似表达式y=φ(x)的方法称为数据拟合，φ(x)称为拟合函数。记拟合函数在xi点的偏差为δi=φ(xi)-yi(i=1,2,…,N)，那么选取φ(x)使所有偏差的平方和最小，即

(14)

这一确定拟合函数的方法称为最小二乘法[10]。

3.2.3 研究结果

由之前的分析得知已完成任务总数为522个。4个地区未完成任务的总和为313个，其中252个分布在广州市和深圳市，因此主要针对广州、深圳两市的情况进行分析。

在深圳和广州两市，未完成任务为252个，已完成任务为229个，对两部分任务的价格进行升序排列，拟合曲线方程为

y=1.6×10-6x3-1.4×10-4x2+1.2×10-2x+65，

(15)

拟合曲线如图4。

可以算出可决系数：

(16)

由可决系数来看拟合的效果比较理想。

由于已完成任务的价格视为不变，因此可以不用考虑重新调整它们的价格。经计算，已完成任务价格均值为69.89元，未完成任务均值为67.93元，因此可以初步判断未完成任务价格偏低。若要改进价格方案，则需适当提高其价格。

从图4中可以看出，在后半部分已完成任务的价格要高于未完成任务，而已完成任务价格不需调整。因此，以已完成任务价格为标准，将拟合曲线方程(15)作为新方案，计算出未完成任务的适当价格，将新方案计算出的价格和原方案的价格进行了比较，对比结果见图5所示。其中现方案代表计算给出的任务价格。

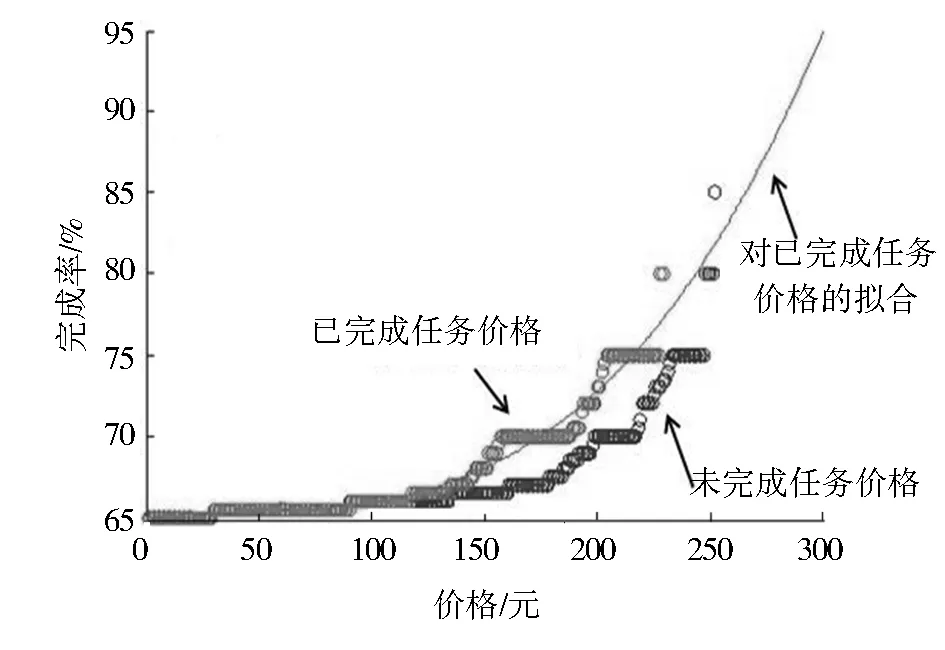
图4 任务价格曲线图Fig.4 Task price curve

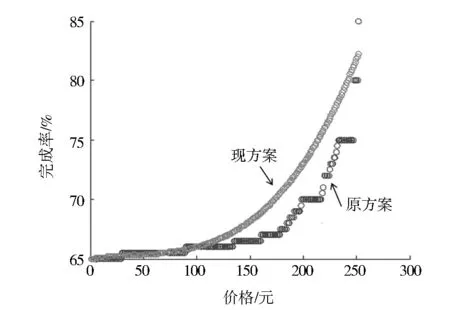
图5 两种方案价格对比图Fig.5 Two pricing options compared

由此，可以看出现方案的价格相较于原方案的价格有了一定程度的提高，其原因在于任务价格的提高对于会员完成任务的积极性起了很大作用，所以当价格上升，会员完成任务的情况也会提高。

同时，该任务价格的均值为69.10元，相较于原来的67.93元有适当提高，因此推断，在此种方案下，任务的完成比例将会增加。

4 结语

针对“拍照赚钱”项目的任务定价，基于K-means均值聚类算法分析区域内会员数量、任务点距离、任务定价与任务完成情况之间的相关性。结果表明：区域内会员数量一定时，完成任务的距离越远，任务定价越高；完成任务的距离一定时，区域内会员数量越小，任务定价越高；在区域内会员数量足够大的前提下，任务定价越高任务完成度越高。基于此进一步深入分析未完成任务，利用最小二乘法拟合出新的定价模型。计算过程中综合利用了MATLAB和EXCEL软件，使计算更加简便准确。K-means均值聚类算法不仅可以解决众包服务定价问题，而且在商业、生物、保险行业等诸多领域都有广泛的运用，具有一定推广意义。