数学教学求“连”，更求“联”——沟通关联，理清内在联系学数学

翁志坚

（文成县第二实验小学，浙江 文成）

一、运用比较，沟通数学知识之间的内在联系

《减法的验算》这节课的教学内容中穿插了这样一道思考题（如下图）：

经过调查发现：大部分同学甚至是老师，不约而同地采用了尝试法，由于是毫无策略的硬凑，以至于重复使用数字的竖式很多，耗时很长，结果很不乐观。 在教研活动上，专门提出了这个问题进行讨论，又上网查阅了相关的材料，终于对这个问题有了更深透地理解。

错误的认识导致解题策略的选择失误，没有好的解题策略，盲目使用尝试法肯定是不行的。为此，首先引导学生研究这样一组简单的试题：

先求和，再找规律。

注意：比较两个加数各位数字之和跟和里的各位数字之和，找出它们之间的规律。

针对此题，我特意从我们学校三年级的四个平行班中随机抽取了100位同学进行调查。调查结果显示：大部分学生对“加数各位数字之和”与“和的各位数字之和”之间的关系都不十分了解，也没有关注过，而且大部分同学对练习过的题目进行归纳的能力较差，所以他们在解答这个问题时不能快速找到突破口，只能采用逐一尝试的方法。

笔者以为：该题的思维起点是：“加数各位数字之和”跟“和的各位数字之和”之间的关系，有了这个基本规律，对这道思考题的解答就可以“信手拈来”。根据竖式中的和与加数的位数不难发现，这道式子最多出现三次进位，最少出现一次进位：

假设一：一次进位

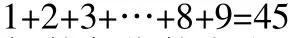
加数各位数字之和：（45+9）衣2=27和的各位数字之和：45-27=18

由于三位数加三位数，和是四位数，和中的最高位必须是1，又因为是最高位一次进位，所以0必须出现在和中，即4个数字分别是：（1、0、8、9），根据交换法，可以变化出许多加法式子：324+765=1089、342+756=1098…

假设二：二次进位

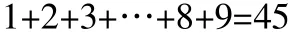
加数各位数字之和：（45+18）衣2=31.5

出现小数，直接排除

假设三：三次进位

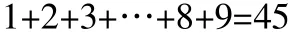
加数各位数字之和：（45+27）衣2=36和的各位数字之和：45-36=9

即和中的 4 个数字分别是：（1、0、5、3），（1、0、2、6），根据交换法，又可以变化出许多加法式子：264+789=1053、437+589=1026…

二、运用一题多解，沟通数学知识之间的内在联系

一题多解，由于解题的方法众多，深受学生喜欢，它可以培养学生思维的灵活性和创造性，并且能促使了解学生知识之间的内在联系。

做过奥数题的同学一定不会忘记“鸡兔同笼”带来的痛楚：

今有鸡兔同笼，头共8个，足共20只，求鸡与兔各有多少只？

方法一：用假设法解答是最普遍的：

方法二：用方程会使思路变得简单：

方法三：还有抬腿法也比较实在：

仔细分析，这几种方法还是比较繁杂的，首先计算出来的是鸡的数量，还是兔的数量？有什么规律吗？中、下层学生往往无从下手。另外，对于初学的人，想把每一步的数与形结合起来，难度很大。

为什么我们不去试试，把“实践与应用”跟“图形与几何”结合起来考虑呢？不难发现，鸡兔同笼问题跟求组合图形的面积问题有极其相似的地方。

三、运用正迁移规律，沟通数学知识之间的内在联系

运用知识的正迁移规律，有助于我们学习新知识、解决新问题，有利于沟通数学知识之间的内在联系。例如，在水流问题这一知识版块，里面的概念繁多而复杂，抽象又生僻，我们理解起来感觉很混乱。如何将抽象的“静水速度”“逆水速度”“顺水速度”“水流速度”的内在关系，用直观的线段图简单、明了的表示出来？

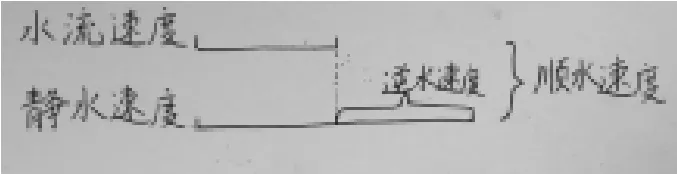
通过这样一个简单的线段图，将水流问题的四个概念与和差问题完美的融合在一起：“水流速度”相当于“较小数”、“静水速度”相当于“较大数”、“逆水速度”相当于“差”、“顺水速度”相当于“和”。水流问题的四个概念间的内在对应联系，便一目了然：

（顺水速度+逆水速度）衣2=静水速度

（顺水速度-逆水速度）衣2=水流速度

静水速度+水流速度=顺水速度

静水速度-水流速度=逆水速度

逆水速度+水流速度伊2=顺水速度

线段图十分直观，利用线段图，可以根据其中的两个条件，求出其他的未知项，十分简便。由于充分运用了正迁移规律，学生不仅很快掌握了“水流问题”，而且沟通了和差问题和水流问题之间的内在联系。

总之，数学是一个多层次、多角度的立体体系，数学知识之间存在着千丝万缕的联系。数学教师只有不断地探索，才能更好地找到沟通数学知识之间的内在联系，不断地使数学教学完整化、系统化。在数学教学中，要根据内容，采取合理的方法，借助适当的形式引导学生去发现数学知识之间的内在联系，进而让学生感悟数学知识的整体性与数学方法的一般性。