基于HYDRUS-1D的不同质地土壤入渗过程数值模拟

刘彬彬，刘尧兵，张科锋

(1. 浙江大学建筑工程学院，浙江 杭州 310058; 2. 浙江大学宁波理工学院，浙江 宁波 315100)

世界上40%的食物是由灌溉农业生产的，消耗全世界70%的淡水资源[1]。然而，目前我国的农业灌溉效率为 45%,仅为发达国家的一半左右, 农业节水潜力巨大[2-3]。农业用水效率的提高对缓解我国水资源短缺现状, 解决供水危机以及保护生态环境具有重要作用。

优化灌溉速率和时间对于节省农业用水至关重要。然而，制定灌溉方案时涉及的因素众多，包括：土壤质地及与之相关的土壤水力特性、作物的根深、根区土壤的含水量以及天气情况等。目前，在优化灌溉的研究方面，土壤水分传感器的应用已日益普遍[4-7]，它可以实时监测土壤剖面不同深度的含水量或水势，有助于做出精确的灌溉策略。但由于埋设的土壤水分传感器数目有限，它们不能精确地确定灌溉后土壤剖面水分分布和最终的润湿深度。此外，传感器的维护和观测均需要一定的技术含量,只适用于土地规模经营的农场。随着土壤科学和计算机技术的发展，数值模拟方法越来越多地应用于土壤水分运动的研究中，已成为定量分析土壤水分入渗特性的有效工具[8-10]。美国国家盐分实验室(US-Salinity laboratory)研发的 HYDRUS-1D 软件，可对一维饱和-非饱和土壤中水、热及溶质运移进行数值模拟[11]。国内外已有诸多文献报道使用HYDRUS软件开展在不同灌溉模式的水分运动和作物根系吸水等方面的研究，取得了可喜的成果[12-15]。但研究仅限于特定的条件，尚未见使用该软件对不同土壤的湿润深度和灌溉量之间关系的系统研究，对指导优化灌溉、节约农业用水局限性明显。

本研究基于HYDRUS-1D软件，针对不同的土质，在不产生地表径流的情况下，系统地模拟灌溉结束时和灌溉结束24 h之后的土壤含水量分布，期望能获得在不同土壤条件下灌溉水分重分布后土壤湿润深度和灌溉量之间的定量关系，为不同根深的作物制定合理的灌溉方案提供参考。

1 模型原理

1.1 土壤水分运动方程

假定土壤为均质、各向同性的多孔介质，忽略温度与土壤中的气相对土壤水分的影响，不考虑根系吸水与源汇项，用以研究饱和-非饱和流动问题的一维Richards控制方程[16]：

(1)

式中,θ是单位体积土壤含水量(cm3·cm-3)；t为时间(h)；z是垂直空间坐标，也可认为是土壤深度(cm)；K是土壤导水率(cm·h-1)；h是土壤压力水头(cm)。

1.2 土壤水力特征参数方程

土壤水力特征参数的描述采用van-Genuchten模型，其表达形式为[17]：

(2)

(3)

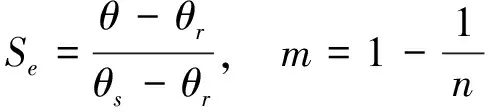
(4)

式中,θs是土壤饱和含水率(cm3·cm-3)；θr是土壤残余含水率(cm3·cm-3)；Ks是饱和导水率(cm·h-1)；α为与进气吸力相关的参数(1·cm-1)；n和m是形状系数；n的大小直接决定着对土壤水分特征曲线的坡度影响；Se为有效含水率；l为经验拟合参数,一般为0.5。

1.3 模型边界条件和初始条件

本模拟是为了研究水分重分布后土壤湿润深度和灌溉水量之间的关系。对淤泥、粉砂壤土、砂质粘壤土三种土质进行了以下的系统模拟：在不产生径流量的情况下，设计在3 h内不同的灌溉速率和时间的组合，得到模拟土层在灌溉结束时和灌溉结束24 h后的水分分布情况，并确定灌溉水分重分布后的土壤湿润深度。

模拟区域为100 cm厚的土壤深度，等分为500层，每层厚度为0.2 cm。模型区域上边界为大气边界，下边界为自由排水边界。由于模拟的持续时间较短，故忽略土壤表面蒸发，同时也不考虑根系吸水作用。

计算区域的初始含水量θ0为土壤有效含水量的中间值，即为田间持水量θFC和永久枯萎点含水量θPWP的中间值[18]。对大部分作物而言，当根区土壤含水量低于θ0时，作物无法获取生长所需的潜在蒸腾量，因而影响作物生长[18]。

1.4 数值实验方案

本数值实验采用的土壤水力特征参数如表1所示[19]，同时表1还列出了田间持水量θFC和永久萎蔫点含水量θPWP。

表1 土壤的水力特性参数Table 1 Soil hydraulic characteristics

2 结果与分析

本研究的结果分两部分，第一部分是验证灌溉后土壤含水量的实测值和模拟值之间的吻合度，以确定用本文提出的数学方法能否较准确地模拟实验结果；另一部分是通过对淤泥、粉砂壤土、砂质粘壤土三种土质的系统模拟，量化不同土质的土壤水分分布与灌溉水量和时间之间的关系。

2.1 灌溉后土壤含水量实测值和模拟值之间的对比

本验证示例取自文献[20]。灌溉实验在直径5 cm、长160 cm的柱体里进行，土质为细砂壤土，密度为1.47 g·cm-3，灌溉量为5 cm和10 cm两种，观测灌溉后不同时间的柱内土壤含水量分布，土壤的水力特征参数和土壤含水量观测方法见文献[20]。本研究取10 cm灌溉量、灌溉1天后的土壤含水量分布作为验证示例。图1显示了土壤含水量实测值和模拟值之间的对比，不难看出土壤含水量实测值和模拟值之间吻合良好，模拟值和实测值之间的R2值达0.9以上，表明两者之间高度相关。

图1 灌溉后土壤含水量实测值和模拟值之间的对比Fig. 1 Comparison of soil water content between measurement and simulation

为客观评价模拟结果，对模拟的土壤含水量值进行了统计分析，计算的统计指标包括：均方根误差(RMSE)、相对均方根误差(RRMSE)、纳什系数[21](NSE)和平均误差(AE)，统计分析结果见表2。从表2中可以发现，RMSE、RRMSE和AE的值均低，说明模拟值和实测值接近；而NSE的值较高，一般认为若NSE的值超过0.75，模型可以被判定为“非常好”。这些统计数据表明了采用本文的数值方法能满意地模拟灌溉后土壤含水量分布。大量的文献也表明HYDRUS-1D模型能较好预测土壤含水量的变化[22-24]。

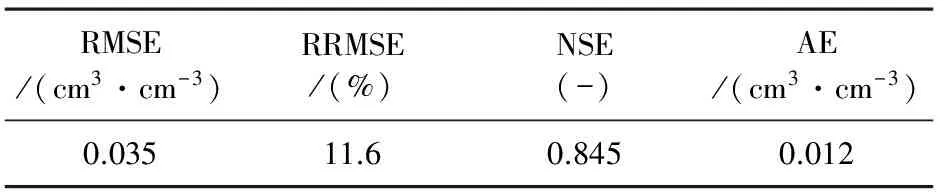
表2 模拟结果的统计分析Table 2 Statistical analysis of simulated results

2.2 不同土质的灌溉模拟分析

为便于表示，将模拟方案统一命名为RxTy，其中，x表示灌溉速率(cm·h-1)，y表示灌溉时间(h)。就淤泥、粉砂壤土、砂质粘壤土三种不同土质，采取了多种灌溉速度和时间的组合进行数值实验。对于淤泥，采取以下9种灌溉组合方案： R0.7T0.5、R0.9T0.5、R0.5T1、R0.6T1、R0.5T1.5、R0.6T1.5、R0.5T2、R0.5T2.3、R0.5T2.6；对于粉砂壤土，9种灌溉组合方案分别是：R0.7T1、R0.7T1.5、R0.7T2、R0.7T2.5、R0.7T3、R0.8T1、R0.8T1.5、R0.9T1、R1.2T0.5；对于砂质粘壤土，灌溉组合方案设计为：R0.9T1、R1T1.5、R1T2、R1T2.5、R1.1T2.8、R1.25T1、R1.25T1.5、R1.25T1.8、R1.45T0.5。

2.2.1 土壤含水量重分布 如上所述，每种土质有9种不同的灌溉速度和时间组合，模拟结果较多。作为比较分析，只选取每种土质的两种灌溉方案(灌溉量较小和较大的各一种)，并予以详细地分析在灌溉过程中和灌溉结束后土壤含水量分布的动态变化，这六种方案分别是：淤泥R0.9T1、0.4T1.5、粉砂壤土R0.9T1、粉砂壤土R0.7T3、砂质粘壤土R0.9T1和砂质粘壤土R1.1T2.8(图2)，灌溉量的变化范围0.6～3.08 cm。

从图2可以很明显地看出，不同的模拟方案中的上层湿润土在灌溉结束时均接近饱和状态，随着深度的增加，从接近饱和区的底部过渡到初始含水量区，含水量骤降，以粉砂壤土R0.7T3方案为例，土壤剖面含水量从0.432 cm3·cm-3下降至初始含水量0.172 cm3·cm-3，土壤深度变化仅为4 cm。另一方面，由于水分重分布的作用，灌溉结束24 h后和灌溉结束时的土壤剖面含水量有很大的差异，在灌溉结束时，灌溉水储存在距表层9.2 cm深的土层中，但经过24 h后，湿润锋向下渗透至20.6 cm，约有55.3%的灌溉水参加了水分重分布。从图2中还可发现，不管何种土质，灌溉结束后土壤水分重分布现象明显，重分布后的土壤含水量更趋均匀，尤其是对于排水性能较好的土质，土壤水分重分布尤为明显。因此灌溉时必须考虑土壤水分重分布的情况，以免造成水资源浪费。

图3显示了地表以下5 cm处土壤含水量随时间的变化，灌溉期间土壤含水量随时间的增加急剧增加，灌溉结束后由于水分重分布的作用，含水量随时间的增长而减少，初期的减少速率大于后期，24 h后基本趋于稳定。以粉砂壤土R0.7T3为例，在3～10 h期间土壤含水量从0.431 cm3·cm-3下降到0.346 cm3·cm-3，而在其后的14 h内，含水量仅下降了0.03 cm3·cm-3。对于同一种土质，灌溉量小的土壤含水量变化较灌溉量大的更为平缓。

此外，还发现对于同一种土质，当灌溉量相同时，不同的灌溉速度在灌溉结束24 h之后土壤剖面的含水量分布相同。这说明了重分布后的土壤含水量只与灌溉量有关，与灌溉速度和时间关系不大。

图2 不同质地土壤含水量的动态分布Fig. 2 Dynamic distribution of soil water content in various soils

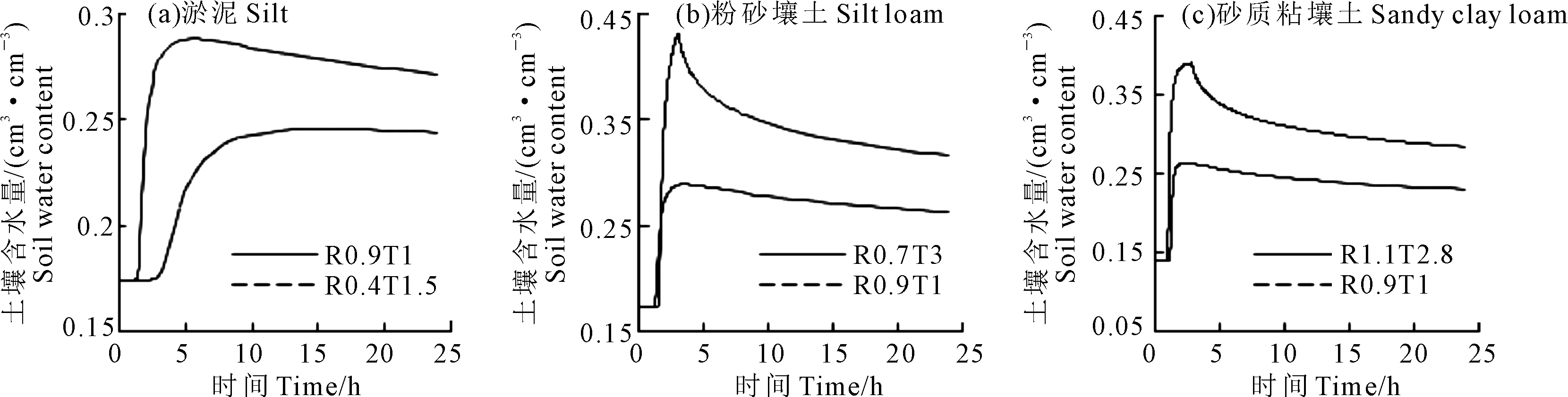
图3 土壤含水量随时间的变化Fig. 3 Variation of soil water content with time

2.2.2 土壤湿润深度与时间和灌溉量的关系 土壤湿润深度与时间的变化如图4所示。不难发现，不同土质间的土壤湿润深度随时间的变化规律类似。灌溉期间土壤的湿润深度随时间的增长而迅速增加，且两者基本呈线性关系，随后在土壤水分重力和毛细孔的作用下，土壤的湿润深度随时间的增加而继续增加，但增速下降。以砂质粘壤土R1.1T2.8为例，在灌溉期间，土壤的湿润深度增加量为14.2 cm，灌溉结束后的前5 h，土壤的湿润深度增加了5.6 cm，但在其后的16 h内，土壤的湿润深度只增加了5.2 cm，尤其在20～24 h期间，湿润深度仅增加了1.0 cm，说明土壤水分重分布在24 h内基本完成。对于同一种土质，在灌溉量小的情况下，土壤含水量的重分布更为平缓。

图4 土壤湿润深度随时间的变化Fig. 4 Variation of soil wetting depth with time

图5显示了三种土质模拟得到的在灌溉结束24 h后灌溉总量和土壤湿润深度的关系。对于不同的土质，其湿润深度与总灌溉量有显著的线性关系，拟合优度R2均在0.99以上，拟合的斜率相差不明显，介于5.15(淤泥)和5.95(砂质粘壤土)之间(见表3)。表3给出了灌溉总量和土壤湿润深度的简单定量关系，该关系对作物生产中的优化灌溉具有实际指导意义。已有研究表明，作物从根深以外的土层中获取水分的能力较弱，因此优化灌溉的目标之一就是要避免过量灌溉导致灌溉水在重分布后流出根区范围。对于不同的作物，已有大量有关作物根系分布方面的研究[25-26]，作物的最大根深可以估计，其根深在生长过程中与累计气温呈线性关系[27-28]，这就允许在作物生长阶段动态地估计作物的根深。在作物根深已知的条件下，通过借助表3中的方程，可以推求出湿润根区土壤所需的水量，为优化灌溉提供科学依据。

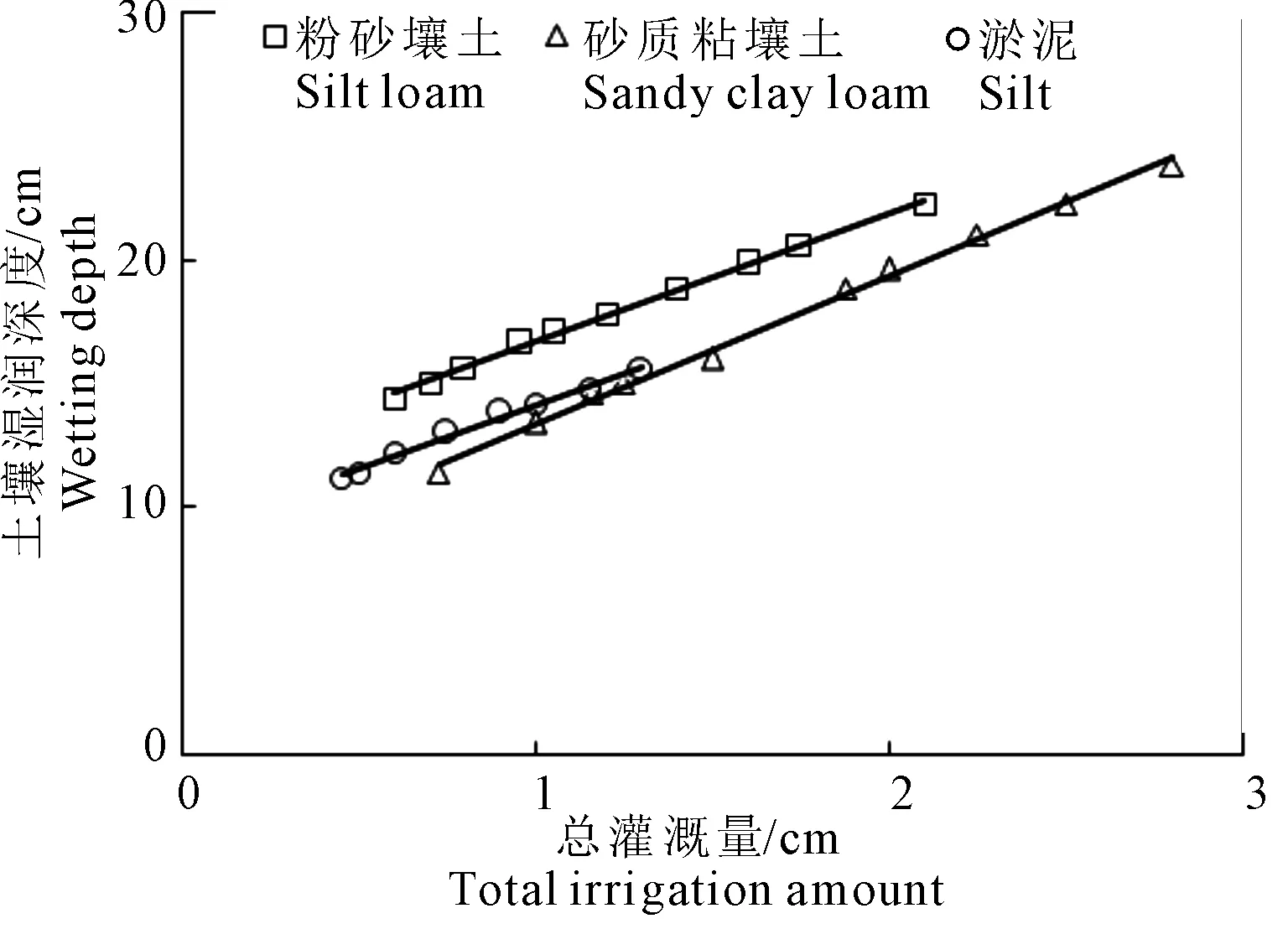
图5 不同质地土壤灌溉结束24 h后的土壤湿润深度与总灌溉量的关系Fig. 5 Relationship between soil wetting depth and total irrigation amount after 24 hours of irrigation

表3 土壤湿润深度与灌溉量间的拟合方程Table 3 Fitted equations relating soil wetting depth and irrigation amount

3 结 论

本文运用HYDRUS-1D软件，采用不同的灌溉速率和灌溉时间组合，对灌溉后不同土质的土壤的土水动力学特性进行了系统的数值模拟试验，量化了在灌溉结束24 h后土壤湿润深度与灌溉总量的关系。基于以上结果，得出了以下几点结论：

1)土壤的含水量分布和湿润深度只与土壤种类和灌溉量有关。对同一种土壤而言，当灌溉量相等时，灌溉结束24 h后土壤含水量分布相同。

2)在灌溉结束后，上层土壤含水量接近饱和，灌溉水储存在上层土壤中。水分重分布后，土壤透水性不同，土壤湿润深度增加不同。因此，对透水性好的土壤在制定灌溉方案时须考虑水分重分布的影响。

3)水分重分布后土壤的湿润深度与灌溉量之间存在着显著的线性关系。该关系可根据灌溉量估计土壤湿润深度，避免灌溉水量过多而产生的水量损失。

本文的研究结果可为不同根深的作物制定合理的灌溉方案提供参考，对作物生产中的水分优化利用有一定的指导意义。