风攻角对强风下大跨度斜拉桥车−桥耦合振动的影响

唐俊峰，何玮，郭向荣，何旭辉，邹云峰



风攻角对强风下大跨度斜拉桥车−桥耦合振动的影响

唐俊峰1，何玮2，郭向荣1，何旭辉1，邹云峰1

(1. 中南大学 土木工程学院，湖南 长沙，410075；2. 安徽建筑大学 土木工程学院，安徽 合肥，230601)

为研究风攻角对强风作用下大跨度斜拉桥车−桥系统耦合振动的影响，通过风洞试验得到不同风攻角条件下桥梁主梁和桥上不同位置处列车的三分力系数；在此基础上，依据弹性系统动力学总势能不变值原理，进一步建立风−车−桥耦合系统振动方程，求解方程并就风攻角对桥梁和列车的动力响应的影响进行分析研究。研究结果表明：风攻角对桥梁和列车的气动三分力系数影响较大；桥梁跨中处的横向振动位移在攻角为−12°时有最大值，竖向振动位移在攻角为−6°时有最大值，极大值均未在攻角为0°时出现；风攻角对车辆动力响应的影响较大，但各项动力响应受风攻角影响而出现变化的趋势并不相同；列车的脱轨系数、轮重减载率和横向力在负向攻角时比正向攻角时的大，且随负向攻角绝对值的增大有增大趋势。

斜拉桥；列车；风攻角；耦合振动；风洞试验

列车在通过大跨度斜拉桥时，若遇强风，将使本已复杂的车−桥耦合振动变得愈加复杂。目前，人们对横风条件下车−桥耦合振动分析研究较多[1−3]。风作为一种自然现象，在吹过桥梁桥面时往往具有一定的风攻角。近年来，一些桥址处风场实测的结果表明，风攻角最大可达10°左右[4]。人们就风攻角对桥梁气动性能的影响进行了研究，如：杨靖等[5]对某大跨度连续梁桥不同截面的三分力系数进行数值模拟计算，发现风攻角对桥梁的静气动性能影响显著；杨群等[6]通过节段模型风洞试验，对宽高比为5的矩形截面梁的气动力特性随风攻角变化的规律进行了研究；张丹 等[7]通过风洞试验研究在不同风攻角下某主梁节段模型三分力系数的雷诺数效应，发现风攻角对流线型桥梁截面三分力系数的雷诺数效应有较大影响；周奇 等[8]通过风洞试验检验了不同风攻角下某斜拉桥颤振临界风速，建议颤振检验风速可按风攻角区间分别确定；GUO等[9]通过风洞试验研究了当风攻角从−6°到6°范围内变化时，车辆和桥梁三分力系数的变化规律。风荷载对车−桥耦合振动的影响已经得到广泛重视和研究[10]，但目前研究多集中在风攻角为0°条件下进行，对风攻角变化对车−桥耦合振动的影响研究较少。为此，本文作者基于以往研究，首先通过斜拉桥主梁和车辆节段模型的风洞试验，获得不同风攻角工况下主梁和车辆的气动三分力系数并分析风攻角对这两者三分力系数的影响；建立风−车−桥系统耦合振动方程，将轨道不平顺作为系统的自激激励源，并将基于风洞试验得到的三分力系数形成的作用在桥梁和列车的风荷载作为外部激励，用逐步积分法求解方程，对风攻角变化对风−车−桥系统耦合振动的影响进行研究。

1 风洞试验

1.1 试验模型

在进行风−车−桥耦合振动计算分析前，需对车桥系统的气动特性进行研究，获得形成风荷载必需的气动三分力系数[2−3]。目前，进行相关研究的方法主要有风洞试验和CFD技术[11−13]，本文的三分力系数由风洞试验获得。风洞试验在中南大学高速铁路风洞试验系统高速试验段完成，试验的节段模型来自某大跨度双塔斜拉桥的主梁。该主梁为采用正交异性桥面板的扁平钢箱梁，其示意图如图1所示。主梁全宽19.60 m，桥梁中心线处梁高3.00 m，宽高比为6.53。

试验中，主梁和车辆节段模型均设计为刚性模型，模型几何缩尺比为 1:40，最大堵塞率为 4.1%，模型外形根据实物尺寸严格按缩尺比缩小，保证其几何相似性。主梁模型横截面宽为49.00 cm，高为7.50 cm，长为200.00 cm，长宽比为4.08；列车为地铁A型车，具体参数见GB 50157—2013“地铁设计规范”[14]。车辆节段模型宽为8.75 cm，高为11.00cm，长为200.00 cm。为保证节段模型具有足够的刚度，模型由高强木板加工而成并在模型内部设置加劲梁；为避免端部效应，在模型两端设置大端板且端板高度大于3倍梁高。

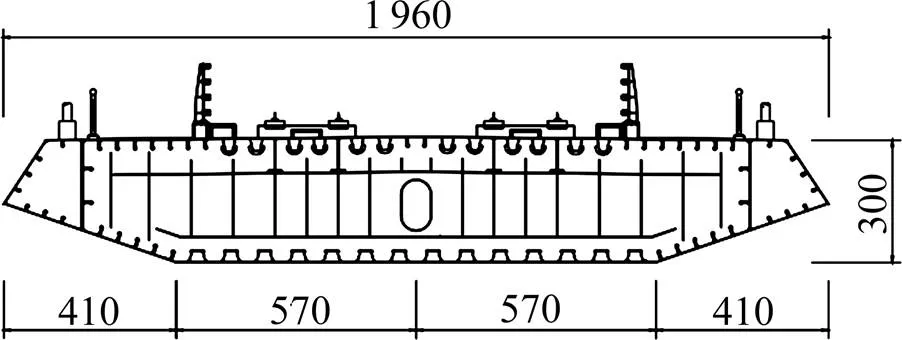
数据单位：cm

1.2 风洞试验结果

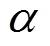
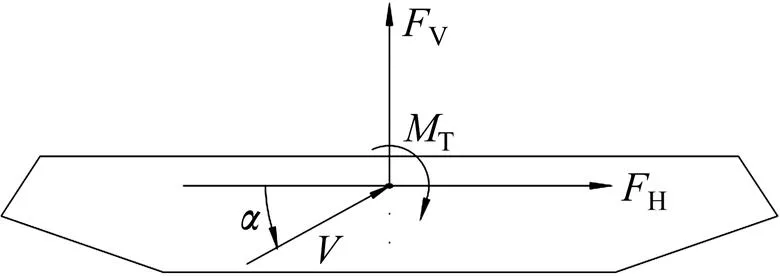
图2 主梁三分力坐标系及风攻角示意图

试验流场为均匀流场，试验时风向角为90°，考虑10 m/s和15 m/s这2种不同试验风速进行相互校核。桥梁和列车气动三分力系数风洞试验结果分别见表1和表2。由表1和表2可知：风攻角方向和角度对桥梁和列车的三分力系数的影响非常明显，当风攻角在−12°~12°范围内变化时，阻力、升力和扭矩系数等呈现的变化规律并不相同，各三分力系数的最大值较少出现在风攻角为0°的情况，而三分力系数的改变势必给强风条件下的风−车−桥耦合振动带来较大影响。从表1和表2还可见：列车在桥面上行驶时，处于迎风侧或背风侧对桥梁和车辆的三分力系数也有较大影响。

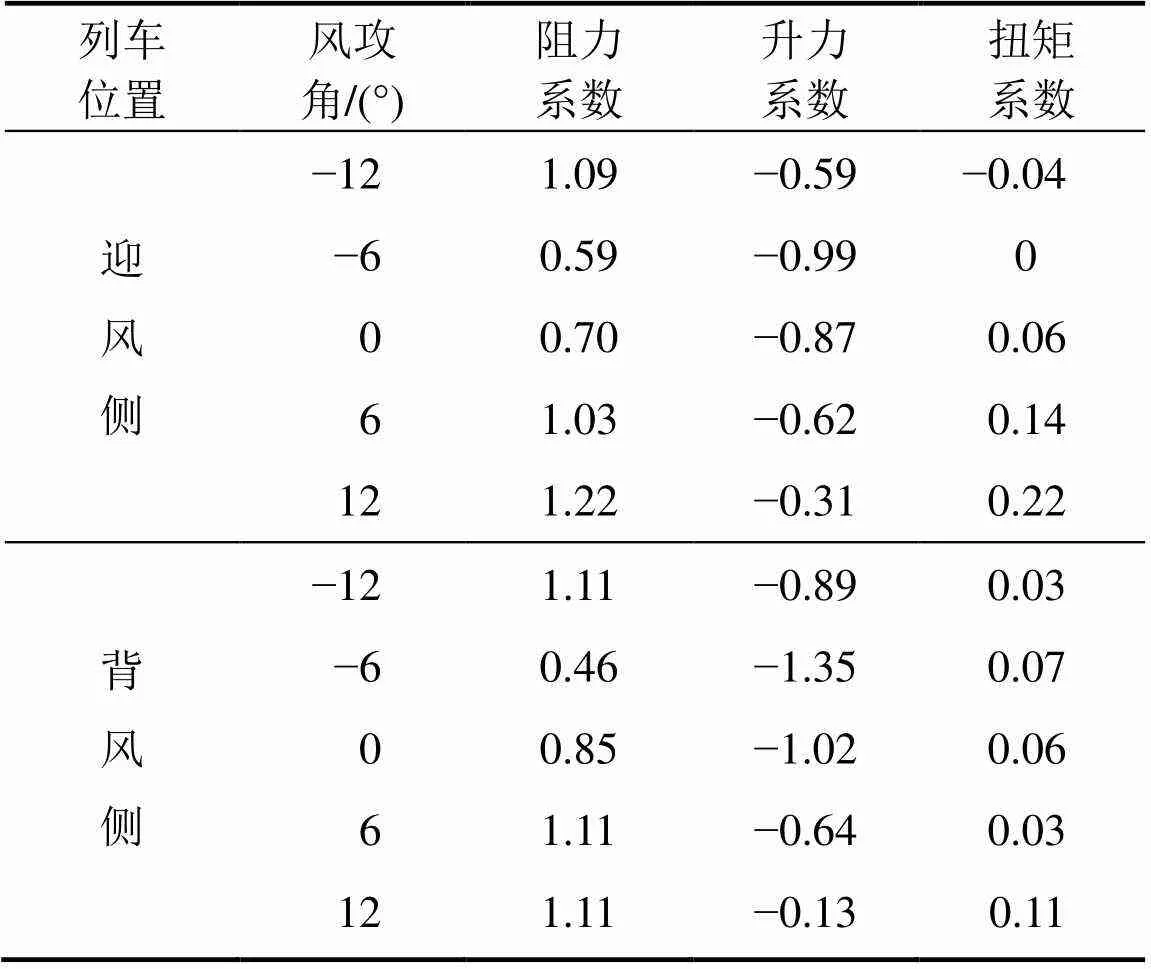
表1 桥梁三分力系数

2 风−车−桥耦合系统计算模型的建立

2.1 列车和桥梁的计算模型

运行中的列车是一个多自由度空间振动的复杂系统，目前，国内外学者在进行车−桥耦合振动分析时建立车辆动力学模型的思路大致相似[15]，为提高计算速度，一般假定车辆箱体、构架和轮对均为刚体，忽略其弹性变形。一般四轴客车的车辆和机车可离散为7个刚体的系统，其中，包括1个车辆的箱体、2个构架和4个轮对，各刚体间由线性弹簧和黏阻尼器相互连接。理论上每个刚体在空间中有6个自由度，故每节四轴车辆共有42个自由度，根据文献[16−18]，在忽略车辆各部件沿桥梁纵向自由度且每个轮对只考虑侧摆、摇头2个自由度后，本文采用的四轴车辆(机车)模型包含23个振动自由度。

斜拉桥的计算模型为空间有限元模型，桥梁的桥塔和桩基础均用空间梁单元离散建模，拉索用杆单元模拟，斜拉桥的主梁未采用空间板单元而是采用梁段有限元建模[16−17]，在车−桥耦合振动分析中，采用梁段有限元方法的特点是能较好地模拟主梁的动力性能的同时，大幅度提高计算效率。桥梁结构的弹性模量和泊松比等参数均按相关的铁路桥梁规范取 值[14]。本文研究的背景桥梁为某大跨度双线铁路斜拉桥，跨径布置为(51+69+340+69+47) m，边跨设置辅助墩。每个桥塔设置13对斜拉索，采用双索面平形布置，跨中设置12 m无索区。该桥采用半漂浮体系，主梁仅在左侧主塔墩处设置固定支座。按上述方法建立的斜拉桥全桥有限元分析模型如图3所示。

2.2 桥梁随机风场的模拟

在建立考虑风荷载的车−桥耦合振动模型时，可将脉动风场近似看作沿斜拉桥主梁长度方向上的若干点随机风波的合成[19]。脉动风场可视为一维多变量的平稳高斯随机过程，计算其互谱密度矩阵并按Shinozuka理论模拟随机过程的样本，见文献[10，20]。模拟风荷载时，考虑斜拉桥桥址处各模拟点之间的空间相关性，沿斜拉桥主梁长度方向上每20 m设1个风速模拟点，共计35点，风速模拟点之间任意点的脉动风速时程可由与之相邻的2个风速点的时程进行线性内插而求得。风速时程样本总长50 s，计算时间步长为0.1 s。图4所示为平均风速为25 m/s时桥梁跨中处的脉动风速时程曲线。

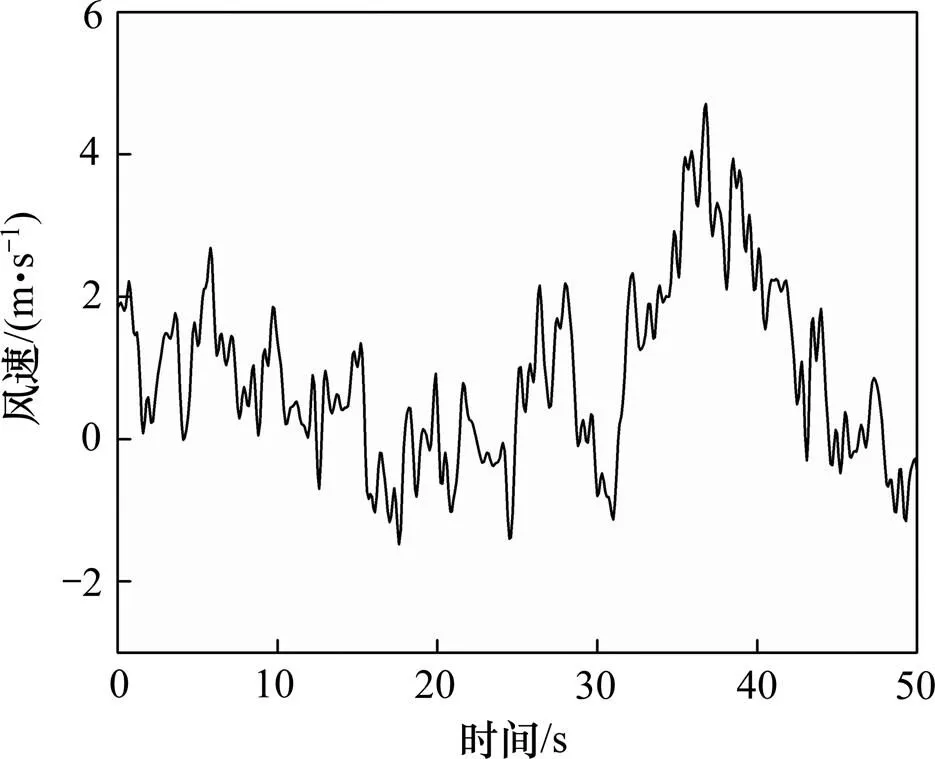
图4 桥梁跨中处的脉动风速时程曲线

2.3 风−车−桥耦合系统的振动方程

在构建考虑风荷载的列车和桥梁耦合系统的空间振动方程时，将列车和桥梁视为1个整体系统，根据线性轮轨蠕滑理论来考虑列车与桥梁之间的横向连接。假定轮轨密贴以考虑列车与桥梁之间的竖向连接，运用弹性系统动力学总势能不变值原理[16, 20]及文献[21]中矩阵的“对号入座”法则，建立的空间振动方程如下：

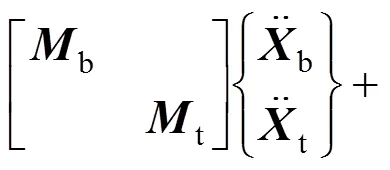
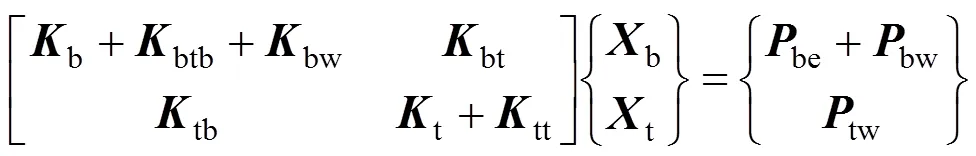
式中：b和t分别为桥梁和列车的质量矩阵；和分别为车−桥系统的阻尼和刚度矩阵，其子项下标代表的意义一致，如b和t分别为桥梁和车辆的阻尼矩阵，btb和tb为由桥梁振动速度所引起的阻尼矩阵，bt和tt为由列车振动速度所引起的阻尼矩阵，bw为由桥梁自身的自激风力所产生的阻尼矩阵；be为列车自重；bw和tw分别为桥梁和列车所受风力。静风荷载所产生的变形在列车上桥前已经完成，故作为车桥系统的初始条件，列车通过桥梁时只在车和桥梁上施加脉动风荷载。列车及桥梁的动力平衡位置是列车上桥前车−桥系统各自的静力平衡位置。

3 风攻角对风−车−桥系统耦合振动的影响分析

在对风−车−桥耦合振动进行计算时，桥面风速取为25 m/s，风向角为90°，考虑的风攻角有0°，±6°和±12°共5种情况，不同风攻角下的桥梁和列车的三分力系数按表1和表2取值。桥上通行列车为地铁A型车，其轴重力为170 kN，列车过桥时分别处于桥面上迎风侧轨道和背风侧轨道单线行车，行驶速度均为 80 km/h。列车采用“动+拖+动+动+拖+动”6辆编组，采用美国六级谱模拟轨道不平顺。

3.1 桥梁动力响应分析

由于斜拉桥中间主跨的跨度为340 m，远大于两侧边跨跨度，所以，对桥梁主跨跨中处节点的振动响应进行分析，计算得到的振动响应包括横向和竖向振动位移与加速度等。计算结果表明：风攻角对桥梁振动加速度影响较小，而对桥梁振动位移影响较大。桥梁跨中的振动位移最大值随风攻角变化如图5所示，振动位移随时间变化如图6和图7所示(其中，“迎风”和“背风”分别指在桥面上处于迎风侧行车和背风侧行车)。

(a) 列车迎风；(b) 列车背风

由图5(a)可知：当列车在迎风侧通过桥梁时，桥梁跨中的横向位移在−6°时有最小值；当风攻角从−6°变化到12°时，横向位移呈逐步增加趋势；当列车在背风侧通行，攻角从−12°变化到6°时，该处的横向位移随风攻角改变而变化的规律与迎风工况的类似，但在6°后呈减小趋势。当列车位于迎风侧或背风侧行车时，桥梁的横向振幅相差较大，这主要由2个原因造成：1) 列车单线行驶在桥上时产生偏载效应，而且该偏载效应将与风荷载产生叠加或者抵消；2) 结合表1和表2中的三分力系数，车辆在桥面横向上的位置对列车和主梁的三分力系数有直接影响，进而影响桥梁的动力响应。从图5(b)可知：桥梁跨中的竖向振动位移随风攻角变化的趋势基本类似，在攻角为−6°时有最大值，然后逐渐减小。竖向位移同样受到车辆在桥面上位置的影响，但不如横向位移受到的影响明显，这是由于竖向位移主要由列车荷载产生。总之，桥梁振动位移受风攻角的影响非常明显。

桥梁跨中横向位移时程曲线见图6。从图6可见：桥梁跨中横向初始位移在不同风攻角条件下有不同的值，其中攻角为6°时的横向初始位移要比攻角为0°和−6°这2种情况下的要大，这是由于攻角为6°时桥梁的阻力系数较大从而使桥梁受到更大的横向风力。另外，桥梁跨中横向初始位移主要由风荷载所致，因为此时列车刚驶入桥梁。可见风荷载对桥梁横向振动位移的影响十分明显。随着列车向桥梁跨中行进，跨中处的横向位移逐步增大，在大约15 s时，头车到达跨中，此时，位移到达最大值。当风攻角为0°和±6°时，桥梁跨中横向位移的时程曲线变化有类似之处，但在各时间点上，攻角为6°时的跨中横向位移均要比其他2个攻角时的大，这也是攻角为6°时桥梁的阻力系数较大所致。桥梁跨中竖向位移时程曲线见图7。从图7可见：桥梁跨中竖向振动位移的时程曲线比较光滑，最大值也产生在列车行驶至跨中时。对比列车刚驶入桥梁和列车行驶至跨中时的竖向位移，跨中处的竖向位移主要由列车荷载产生。与其他2种风攻角工况相比，攻角为−6°时竖向位移较大，这是由于此时桥梁的升力系数绝对值较大。

3.2 车辆动力响应分析

当桥面风速为25 m/s，列车以速度80 km/h通过桥梁时，列车从头车上桥到尾车驶离桥梁，在整个过程中，车辆动力响应最大值随风攻角的变化如图8所示。图8中车辆动力响应包括脱轨系数、轮重减载率、横向力、车体横向和竖向振动加速度等的响应。

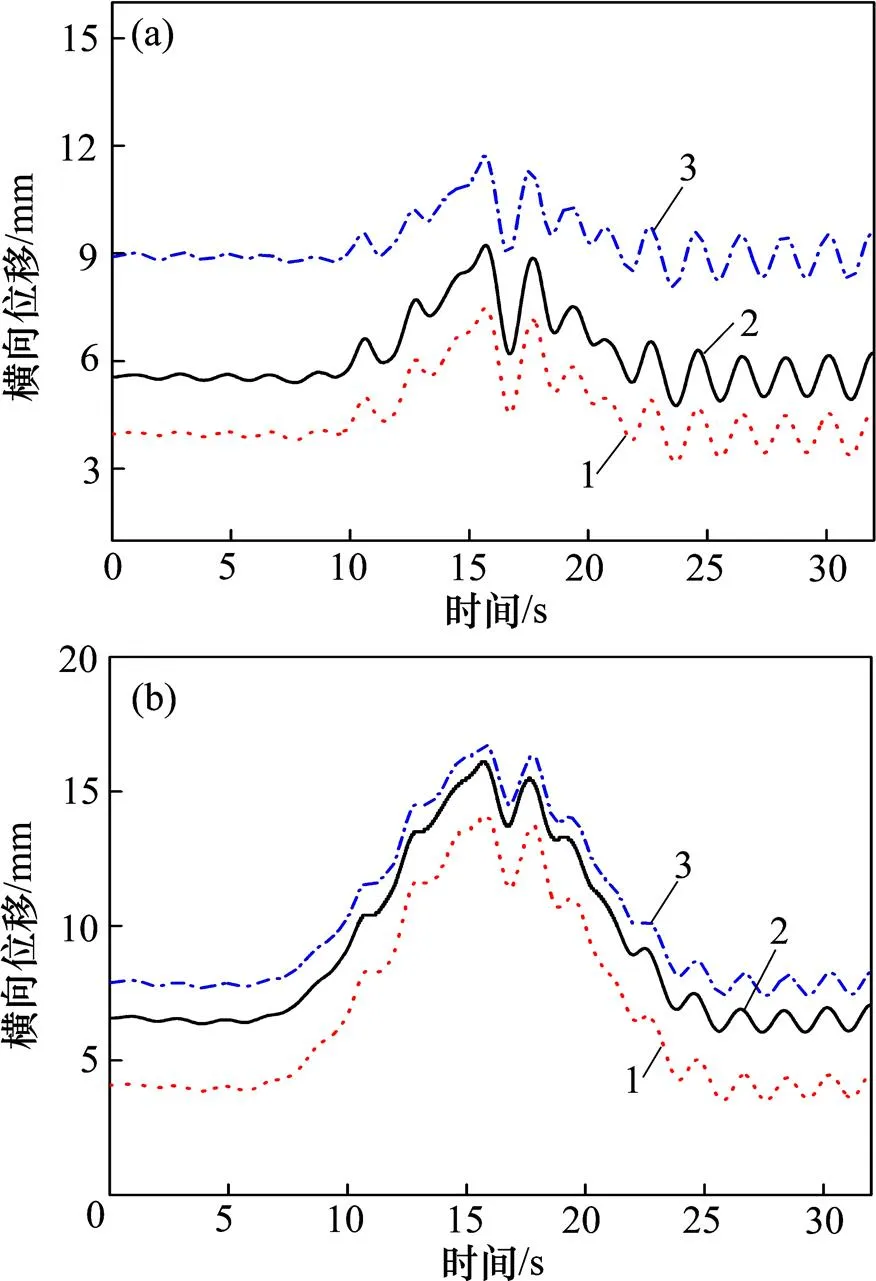
(a) 列车迎风；(b) 列车背风

(a) 列车迎风；(b) 列车背风

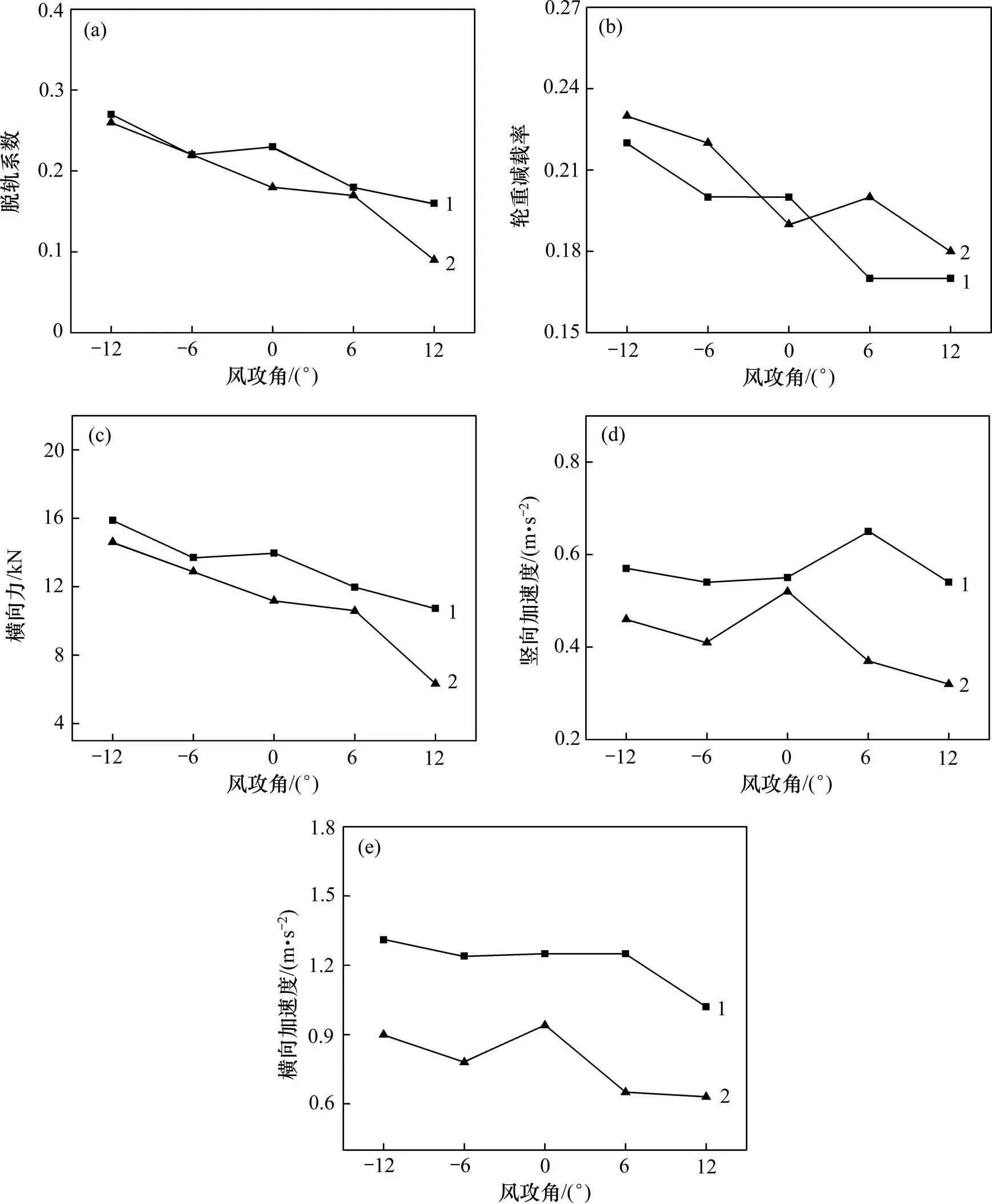
(a) 脱轨系数与风攻角的关系；(b) 轮重减载率与风攻角的关系；(c) 横向力与风攻角的关系；(d) 竖向加速度与风攻角的关系；(e) 横向加速度与风攻角的关系

从图8(a)可见：当列车位于迎风侧时，随着风攻角从−12°变化到12°，脱轨系数大体上呈减小趋势，但在风攻角为0°时小幅度增大；当列车位于背风侧时，脱轨系数随风攻角的变化逐渐减小，当风攻角从6°增大到12°时，脱轨系数迅速减小。当列车位于迎风侧或背风侧，风攻角为−12°时，脱轨系数均有最大值；当风攻角为12°时，脱轨系数均有最小值。从图8(b)可见：随着风攻角从−12°变化到12°，迎风侧行车列车的轮重减载率逐渐减小。背风侧行车情况则相对复杂。从图8(c)可见：当风攻角从−12°变化到12°时，轮轴横向力大致上呈逐步减小趋势，列车处于迎风侧行车时的横向力要比背风侧行车时的大。总体上讲，脱轨系数、轮重减载率和横向力在负向攻角比正向攻角时要大，且随负向攻角绝对值的增大有增大趋势，故列车在桥上通行若遭遇强风且风攻角为负向大攻角时，列车动力响应将偏大，则相应的列车行车安全性需引起重视。

从图8(d)可见：车体竖向振动加速度随风攻角的改变而变化的规律比较复杂。当列车位于迎风侧行车时，竖向加速度的最大值出现在风攻角为6°时，而列车位于背风侧时其最大值出现在攻角为0°时。从图8(e)可见：当列车处于迎风侧时，车体横向加速度最大值出现在风攻角为−12°时，然后，随角度的变化大致呈减小趋势；当列车在背风侧行车时，车体横向加速度随风攻角变化的规律相对复杂，最大值出现攻角0°时。当列车在风攻角较小或者横风条件下通过桥梁时，列车车体加速度更有可能出现较大值。

4 结论

1) 风攻角的方向和大小对桥梁和列车的气动三分力系数有明显影响，因此，有必要对风攻角变化对风−车−桥耦合振动的影响进行研究。

2) 当列车通过桥梁时，桥梁跨中处横向振动位移最大值出现于攻角为−12°时，最小值为出现于攻角为−6°时，竖向振动位移最大值出现在攻角为−6°时，最小值出现在攻角为12°时，极大值均未在攻时为0°时出现。当风攻角为6°时，桥梁横向振动的初始位移明显比攻角为0°和 −6°时的大，这是由于6°时桥梁的阻力系数较大从而所受风力较大；在攻角为−6°时，竖向位移较大，这是由于−6°攻角时桥梁的升力系数绝对值较大。

3) 风攻角对列车的动力响应有显著影响，但各项动力响应受风攻角影响而出现变化的趋势并不相同。脱轨系数、轮重减载率和横向力在负向攻角时比正向攻角时要大，且随负向攻角绝对值的增大呈增大趋势，因此，列车在负向风攻角强风条件通过桥梁时，行车安全性需引起重视。车体加速度的最大值出现在风攻角较小时。

4) 列车在通过桥梁时处于桥面上的迎风侧或者背风侧对桥梁和车辆的三分力系数有明显影响，对桥梁和车辆的动力响应也有较大影响，可见列车在桥面上的行车位置增加了风−车−桥耦合振动的复杂性。

5) 风攻角对强风条件下车−桥耦合振动的影响比较明显，车辆和桥梁的动力响应最大值往往并未在攻角为0°时出现。为了安全，当大跨度桥梁存在较大风攻角且不能忽视的情况下，建议通过风洞试验研究不同风攻角对车辆、桥梁气动性能的影响，并基于此对风−车−桥耦合振动进行研究。

[1] DINH V N, KIM K D, WARNITCHAI P. Dynamic analysis of three-dimensional bridge–high-speed train interactions using a wheel–rail contact model[J]. Engineering Structures, 2009, 31(12): 3090−3106.

[2] XIA He, GUO Weiwei, ZHANG Nan, et al. Dynamic analysis of a train–bridge system under wind action[J]. Computers & Structures, 2008, 86(19/20): 1845−1855

[3] 张敏, 张楠, 夏禾. 大跨度铁路悬索桥风−车−桥耦合动力分析[J]. 中国铁道科学, 2013, 34(4): 14−20. ZHANG Min, ZHANG Nan, XIA He. Analysis on wind−vehicle−bridge dynamic interaction for long-span railway suspension bridge[J]. China Railway Science, 2013, 34(4): 14−20.

[4] 陈政清. 桥梁风工程[M]. 北京: 人民交通出版社, 2005: 40−65. CHEN Zhengqing. Bridge wind engineering[M]. Beijing: China Communications Press, 2005: 40−65.

[5] 杨靖, 何旭辉, 冉瑞飞, 等. 高速铁路连续梁桥三分力系数的数值模拟分析[J]. 铁道科学与工程学报, 2013, 10(1): 11−15.YANG Jing, HE Xuhui, RAN Ruifei, et al. Numerical simulation analysis of tri-component force coefficient of continuous beam bridge on high-speed railway[J]. Journal of Railway Science and Engineering, 2013, 10(1): 11−15.

[6] 杨群, 刘小兵. 风攻角对宽高比为5的矩形断面梁气动力特性的影响[J]. 石家庄铁道大学学报(自然科学版), 2015, 28(1): 6−11.YANG Qun, LIU Xiaobing. Influence of wind attacking angle on aerodynamic characteristic of rectangular girder with aspect ratio 5[J]. Journal of Shijiazhuang Tiedao University(Natural Science), 2015, 28(1): 6−11.

[7] 张丹, 李加武, 徐洪涛. 流线型桥梁断面雷诺数效应[J]. 土木工程与管理学报, 2015, 32(4): 67−72.ZHANG Dan, LI Jiawu, XU Hongtao. Reynolds number effect of streamline-like bridge deck section[J]. Journal of Civil Engineering and Management, 2015, 32(4): 67−72.

[8] 周奇, 郭震山, 冯云成, 等. 深切峡谷底斜拉桥颤振稳定性能研究[J]. 山东建筑大学学报, 2014, 29(2): 131−136.ZHOU Qi, GUO Zhenshan, FENG Yuncheng, et al. Experimental study on flutter performance of cable-stayed bridge at the bottom of a deep-cutting gorge[J]. Journal of Shandong Jianzhu University, 2014, 29(2): 131−136.

[9] GUO Weiwei, WANG Yujing, XIA He, et al. Wind tunnel test on aerodynamic effect of wind barriers on train-bridge system[J]. China Technology Science, 2015, 58(4): 219−225.

[10] 郭向荣, 何玮, 朱志辉, 等. 横风作用下货物列车通过大跨度铁路斜拉桥的走行安全性研究[J]. 中国铁道科学, 2016, 37(2): 41−47.GUO Xiangrong, HE Wei, ZHU Zhihui, et al. Running safety of freight train passing long-span cable-stayed railway bridge under cross wind[J]. China Railway Science, 2016, 37(2): 41−47.

[11] XIANG Huoyue, LI Yongle, WANG Bin. Aerodynamic interaction between static vehicles and wind barriers on railway bridges exposed to crosswinds[J]. Wind & Structures an International Journal, 2015, 20(2): 237−247.

[12] XIANG Huoyue, LI Yongle, WANG Bin, et al. Numerical simulation of the protective effect of railway wind barriers under crosswinds[J]. International Journal of Rail Transportation, 2015, 3(3): 151−163.

[13] 张亮, 张继业, 张卫华. 高速列车通过声屏障的流固耦合振动响应分析[J]. 动力学与控制学报, 2014, 12(2): 153−159.ZHANG Liang, ZHANG Jiye, ZHANG Weihua. Analysis on fluid-structure interaction vibration of high-speed train passing by sound barrier[J]. Journal of Dynamically and Control, 2014, 12(2): 153−159.

[14] GB 50157—2013, 地铁设计规范[S].GB 50157—2013, Code for design of metro[S].

[15] 翟婉明, 夏禾. 列车−轨道−桥梁动力相互作用理论与工程应用[M]. 北京: 科学出版社, 2011 : 64−106.ZHAI Wanming, XIA He. Train-track-bridge dynamic interaction: theory and engineering application[M]. Beijing: Science Press, 2011: 64−106.

[16] 杨仕若, 曾庆元. 铁路车桥耦合振动模态法分析[J]. 深圳大学学报(理工版), 2011, 28(2): 131−135.YANG Ruoshi, ZENG Qingyuan. Coupling vibration analysis of vehicle−bridge by mode method[J]. Journal of Shenzhen University(Science & Engineering), 2011, 28(2): 131−135.

[17] 罗浩, 郭向荣. 多跨斜交简支T梁桥车桥耦合振动分析[J]. 中国铁道科学, 2009, 30(4): 36−40. LUO Hao, GUO Xiangrong. Analysis on the vehicle-bridge coupling vibration of multi-spans skew simply-supported t-beam[J]. China Railway Science, 2009, 30(4): 36−40.

[18] 何玮, 郭向荣, 邹云峰, 等. 风屏障透风率对侧风下大跨度斜拉桥车−桥耦合振动的影响[J]. 中南大学学报(自然科学版), 2016, 47(5): 1715−1721.HE Wei, GUO Xiangrong, ZOU Yunfeng, et al. Effect of wind barrier porosity on coupled vibration of train-bridge system for long-span cable-stayed bridge in crosswind[J]. Journal of Central South University(Science and Technology), 2016, 47(5): 1715−1721.

[19] 曹映泓, 项海帆, 周颖. 大跨度桥梁脉动风场的随机模拟[J]. 土木工程学报, 1998, 31(3): 72−78.CAO Yinghong, XIANG Haifan, ZHOU Yin. Stochastic simulation of wind turbulence field for a long−span bridge[J]. China Civil Engineering Journal, 1998, 31(3): 72−78.

[20] 苗永抗. 超大跨度公轨两用斜拉桥风−车−桥耦合振动研究[D]. 长沙: 中南大学土木工程学院, 2014: 27−32.MIAO Yongkang. Studies on coupled vibration of wind− vehicle−bridge cable-stayed bridge with a super span under wind loads[D]. Changsha: Central South University. School of Civil Engineering, 2014: 27−32.

[21] 曾庆元, 杨平. 形成矩阵的“对号入座”法则与桁段有限元法[J]. 铁道学报, 1986, 8(2): 48−59.ZENG Qingyuan, YANG Ping. The “set-in-right-position” rule for formulating dynamic system matrix and the finite element method of truss section for spatial analysis of truss girder[J]. Journal of the Chinese Railway Society, 1986, 8(2): 48−59.

Influence of wind attack angle on vehicle-bridge coupling vibration for long-span cable-stayed bridge during strong wind

TANG Junfeng1, HE Wei2, GUO Xiangrong1, HE Xuhui1, ZOU Yunfeng1

(1. School of Civil Engineering, Central South University, Changsha 410075, China;2. School of Civil Engineering, Anhui Jianzhu University, Hefei 230601, China)

In order to study the effect of wind attack angle on the coupling vibration of train-bridge system for long-span cable-stayed bridge during strong wind, by using wind tunnel tests, three-component force coefficients of the bridge girder and the train at different positions of the bridge deck and different wind attack angles were obtained. According to the principle of the total potential energy with stationary value in elastic system dynamics, the coupling vibration equation of the wind-train-bridge system was established. The vibration equation was solved and the effect of wind attack angle on the dynamic response of the bridge and train was analyzed. The results show that three-component coefficient of the bridge and train is greatly influenced by the wind attack angle. The transverse vibration displacement at the middle span of the bridge has a maximum value when the attack angle is −12°, and the vertical vibration displacement has a maximum value when the attack angle is −6°, and the maximum values do not appear when the attack angle is 0°. The wind attack angle has a great influence on dynamic responses of the train, but the changing trend of various dynamic responses under the influence of wind attack angle is not the same. Derailment factors, offload factors and lateral forces of the train are larger in the negative attack angle than those of the positive attack angle, and they increase with the increase of the absolute value of negative attack angle.

cable-stayed bridge; train; wind attack angle; coupling vibration; wind tunnel test

10.11817/j.issn.1672-7207.2018.07.024

U441

A

1672−7207(2018)07−1760−08

2017−07−12；

2017−09−22

国家自然科学基金资助项目(51322808，51508580) (Projects(51322808, 51508580) supported by the National Natural Science Foundation of China)

何玮，博士，讲师，从事车−桥耦合振动分析研究；E-mail: hw0920@126.com

(编辑 陈灿华)