基于事故树-层次分析法对中小学校园踩踏事故致因的研究

刘 上，刘 春，吴先勤，陈 丹

(重庆科技学院安全工程学院，重庆 401331)

2017年3月，河南濮阳第三实验小学发生了踩踏事故，让中小学校园踩踏问题重新得到社会的重视。由于中小学校园内聚集了大量的未成年人，且校园的主要活动场所为教学楼等相对狭小的空间场所，这些因素增加了校园踩踏事故(事件)发生的可能性[1]。一旦发生校园踩踏事件，往往会出现群体性伤亡，并且未成年人受到社会的关注度较高，造成的社会影响巨大。国外鲜有针对中小学校园踩踏事件的报道与研究[2]，最近几年我国中小学校园踩踏事件虽多有发生(见表1)，但其致因分析研究较少见，目前国内对踩踏事故的研究多集中于人流量较大的车站、广场等公共场所[3-5]。因此，有必要通过对中小学校园踩踏事故的调查分析，从根本上剖析踩踏事故发生的机制，并提出相应的安全控制策略，这对中小学校园安全建设具有重要的意义。

表1 2009—2017年我国中小学校园踩踏事件统计表Table 1 Statistics of stampede accidents on primary and middle school campus in China from 2009—2017

1 中小学校园踩踏事故发生的机制分析

本文以云南省昆明市明通小学发生的踩踏事件为例,分析了中小学校园踩踏事故发生的机制。首先，该事故发生地点为午休楼，该楼为原普通居民住宅楼改建而成，改建过程中未按照《中小学校设计规范》(GB 50099—2011)进行改建，导致楼道口无法满足大量学生进出的要求;其次，该校体育老师将体育课所用的海绵垫侧放于楼道一侧，这直接导致了事故悲剧的发生;最后，当同学经过该楼道上课时，海绵垫倾倒阻塞道路并导致一部分同学摔倒，而后面的同学不知前面的状况依旧拥挤前进，因而造成了踩踏事件的发生[6]。在这起事故中违规改建的午休楼是造成事故的根本原因，侧放的海绵垫是事故的直接原因，拥挤的人群是事故的间接原因，这些原因共同作用，最终导致了该事故的发生。踩踏事故是指在相对狭小的空间内短时间聚集了大量人员，在第三方因素的影响下，造成人员无序移动，在移动过程中导致人员受伤或死亡的事故[7]。从踩踏事故的定义中可以看出，踩踏事故的发生需要3个基本条件：相对狭小的空间、大量的人员、第三方因素。在中小学校园里相对狭小的空间包括教室、楼道、楼梯、厕所、活动教室、操场等；上课、运动会、餐厅进餐等活动会造成大量人员在短时间内聚集；第三方因素则包括下课、放学、放假或者火灾、地震等导致人员移动的因素。

2 事故树-层次分析法

2.1 事故树-层次分析法简介

事故树是指从结果到原因描述事件发生的有向逻辑树，事故树分析是从结果开始分析，寻求顶上事件发生的原因事件，通过由果找因的方法找到事故发生的直接原因和潜在原因[8]。事故树分析法在描述因果关系中具有逻辑性强、思路清晰且可以定量分析等特点，但是在一些基本事件发生概率无法清楚定量的情况下，事故树的定量分析结果往往偏差较大，因此需要引入层次分析法作为定量分析的手段。所谓层次分析法，就是将一个评价对象划分为几个层次，选择合适的定性指标模糊量化方法计算出其权重值，进而得到层次单排序和层次总排序，作为优化决策方案的安全评价方法[9-10]。将事故树分析法与层次分析法相结合，用于确定事故综合评价中的权重系数，既能够保证评价因素全面有条理，又能够使定性分析定量化，能够有效地提高事故分析的质量和效率。

2.2 事故树-层次分析法的步骤

事故树-层次分析法的基本步骤如下：

(1) 构建事故树模型。依照事故树编制的方法，确定顶上事件，调查分析导致顶上事件发生的各子事件，以此类推直至找到基本事件。各个基本事件全部找齐之后绘制事故树，确定各基本事件之间的逻辑关系，并建立事故树模型。

(2) 构建层次分析模型。通过深入分析事故树的各基本事件，依照事故树的逻辑顺序，将事故树的事件按照目标层、准则层、指标层划分归类，建立层次分析模型。

(3) 影响因素权重计算。影响因素权重计算过程如下：①构建判断矩阵：构造判断矩阵要从上至下，选定上一层次的某一个因素，将本层次的各因素关于这个指定因素进行两两比较，根据评价对象实际情况以及评价目的和要求，选用合适的标度对判断矩阵因素给出合理的赋值，从而构造出一个由重要性比值构成的正互反判断矩阵[11]。本文采用的标度为1～9标度，详见表2。

表2 1～9标度表Table 2 1～9 scale table of Analytical Hierarchy Process

②计算因素的相对权重：仅仅得到判断矩阵，并不能反映出本层次各因素的重要程度，所以还需要计算本层次所有因素的相对权重，通过数学方法求解特征向量，进而得到各因素的相对权重值。由于计算工作量过大，本文采用数学模拟软件MATLAB求解各种参数。

③一致性检验：在构造正互反判断矩阵时，由于评价系统的复杂性，加上对因素进行两两比较时由于受主观意识的影响，构造的判断矩阵往往与实际情况有差异，因此要判断不一致程度是否在可允许范围内，就需要对判断矩阵进行一致性检验。一致性检验过程如下：首先利用MATLAB软件按下式计算一致性指标CI：

(1)

式中：n为判断矩阵的阶数;λmax为最大特征根。

然后判断计算出的一致性指标CI是否有偏差，且偏差是否在允许的一致性范围内，这些问题就需要引入平均随机一致性指标RI来衡量，RI取值详见表3。

表3 RI取值表Table 3 Numerical values of RI

最后按下式计算一致性比例CR：

(2)

当CR<0.1时，认为判断矩阵与实际情况保持一致，则一致性检验通过，说明特征向量W能够表示权重向量;反之，当CR≥0.1时，说明判断矩阵与实际情况存在较大偏差，需要对正互反判断矩阵做适当修正。

(4) 结果分析。当各层因素权重计算完成后汇总成表，按权重值从高到低排序，重点分析权重值较高的因素，并从重点关注因素出发，提出控制和改进的措施。

3 实例应用与分析

3.1 建立事故树模型

通过查阅前人资料和对近几年中小学校园踩踏事故的分析，依照事故树编制的原则和方法，建立了中小学校园踩踏事故树模型，如图1所示，各基本事件及其含义见表4。

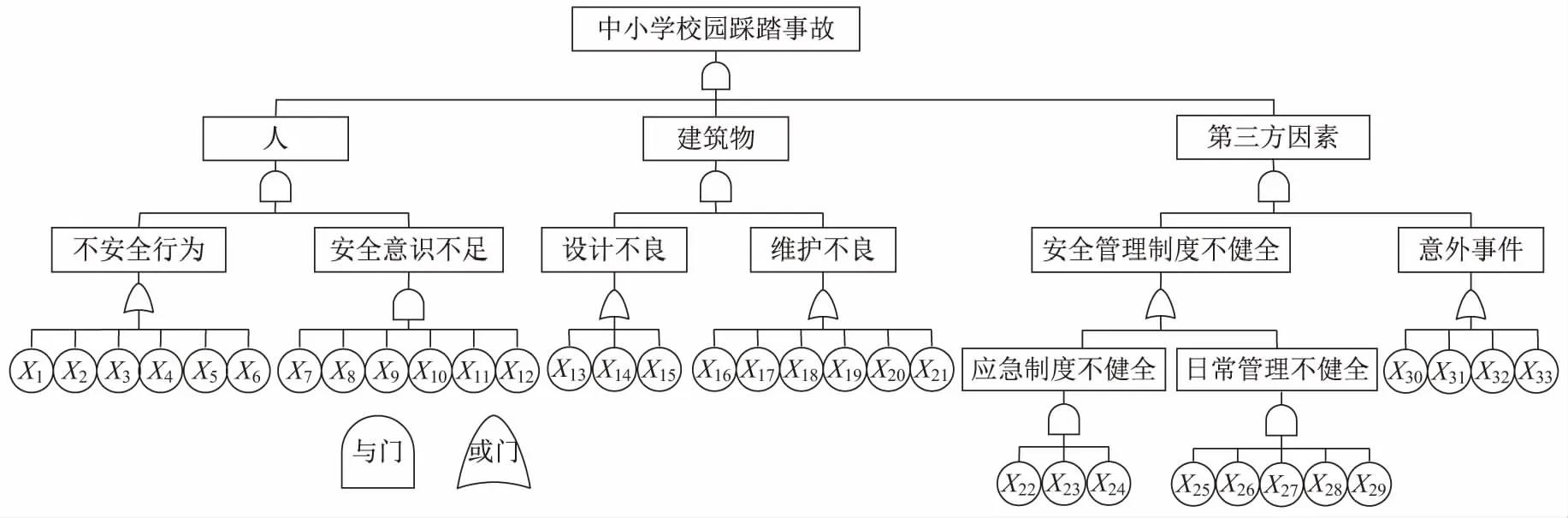
图1 中小学校园踩踏事故树模型Fig.1 Fault tree model of stampede accidents on primary and middle school campus

表4 中小学校园踩踏事故的基本事件及其含义Table 4 Symbols and meanings of basic events of stampede accidents on primary and middle school campus

由图1可见，导致中小学校园踩踏事件发生的主要影响因素有以下5类：

(1) 硬件设施不足B1：包括楼梯设计不合理X13、楼道设计不合理X14、教室分布不合理X15、未预留应急通道X16、缺少应急设备X17、未张贴应急标识X18、栏杆不牢固X19、地面不防滑X20、照明不足X21。

(2) 不安全行为B2：包括恶作剧X1、逆向运动X2、弯腰系鞋带X3、打闹起哄X4、上下楼梯跑动X5、互相推搡X6。

(3) 安全意识不足B3：包括通道堆放杂物X7、不清楚危害性X8、不能识别危险因素X9、恐慌心理X10、不具备应急意识X11、教师缺乏责任心X12。

(4) 安全管理制度不健全B4：包括无应急预案X22、应急预案可操作性不强X23、未进行应急演练X24、安全教育培训不到位X25、班级人数超额X26、时间安排不合理X27、安全组织架构不合理X28、无安全检查制度X29。

(5) 意外事件B5：包括断电X30、地震X31、火灾X32、恶劣天气X33。

3.2 建立层次分析模型

结合图1事故树模型，依照层次分析法层层递阶的原则，建立层次分析模型。其中，以中小学校园踩踏事故作为层次分析模型中的目标层；以硬件设施不足、不安全行为、安全意识不足、安全管理制度不健全和意外事件作为准则层；以事故树中的基本事件作为指标层。构建的中小学校园踩踏事故层次分析模型详见图2。

3.3 影响因素权重计算

本文将事故树的中间事件作为准则层，从硬件设施不足、不安全行为、安全意识不足、安全管理制度不健全、意外事件5个影响因素考量，构建了准则层判断矩阵B：

图2 中小学校园踩踏事故层次分析模型Fig.2 Analytical Hierarchy Process model of the stampede accidents on primary and middle school campus

表5 A—B判断矩阵及各因素的权重值Table 5 Judgment matrix A—B of criterion layer and weight of each factor

依照相同方法，构建指标层判断矩阵，并利用MATLAB软件计算各因素权重、一致性指标CI、一致性比例CR，以及对判断矩阵进行一致性检验，将计算数据整理后见表6至表10。

表6 B1—C指标层判断矩阵及各因素的权重值Table 6 Judgment matrix B1—C of index layer and weight of each factor

表7 B2—C指标层判断矩阵及各因素的权重值Table 7 Judgment matrix B2—C of index layer and weight of each factor

表8 B3—C判断矩阵及各因素的权重值Table 8 Judgment matrix B3—C of index layer and weight of each factor

表9 B4—C判断矩阵及各因素的权重值Table 9 Judgment matrix C4 of index layer and weight of each factor

表10 B5—C判断矩阵及各因素的权重值Table 10 Judgment matrix B5—C of index layer and weight of each factor

为了能够更加直观地对比各影响因素的重要程度，本文引入百分制表格，利用已算出各因素的权重值，以指标层中第1个因素为例，计算其在准则层中的重要程度分值。已知目标层f11=1，准则层f21=0.469 3，指标层f31=0.336 0，利用下式可计算该影响因素重要程度的分值，即

Vi=f11×f2i×f3i×100

(3)

式中：Vi为第i个因素的重要程度分值；f11为目标层权重;f2i为准则层第i个因素的权重;f3i为指标层第i个因素的权重。

最后计算得到V1=15.76%。同理，可求出V2～V33的值，其计算结果见表11。

表11 中小学校园踩踏事故各影响因素的重要程度分值计算结果Table 11 Importance score of influence factors

3.4 评价结果分析

由表11可知，在导致中小学校园踩踏事件发生的5个影响因素中，硬件设施不足所占权重为0.469 3，人的不安全行为和安全意识不足所占权重为0.405 4，这说明建筑物的不安全状态和人的不安全行为因素是导致中小学校园踩踏事件发生的主要原因；同时重要程度分值较高的5个影响因素分别为楼梯设计不合理、通道堆放杂物、恶作剧、楼道设计不合理、栏杆不牢固，这也与现实中中小学校园踩踏事件发生原因的调查结果相一致。对中小学校园踩踏事件进行定量风险评价与分析，是确保校园生活安全有序的重要手段。本文基于事故树-层次分析方法从事故树入手，探究中小学校园踩踏事件发生的原因，并利用层次分析法对踩踏事件进行了定量化描述，其评价结果与实际情况吻合度较好，证明了该方法在校园踩踏事件防控领域具有较为广泛的应用价值。

4 中小学校园踩踏事故的防控策略

通过上述对中小学校园踩踏事件进行定量评价可知，中小学校园踩踏事件的发生是由众多因素共同作用的结果，单一因素并不能导致踩踏事件的发生，因此在制定该类事故预防策略时应从各个因素角度出发，并综合考量，具体的防控措施与建议如下：

(1) 中小学建筑物设计、施工、改建要严格按照《中小学校设计规范》(GB 50099—2011)相关规定实施，尤其是楼梯、楼道等相对狭小但人流量较大的场所必须根据实际情况进行扩容。

(2) 学校要制定安全检查计划，定期对校园内容易发生踩踏事故的场所进行安全检查，检查项目要囊括安全设施状态、照明、标识、监控等各个方面。

(3) 学校要加强全校人员的安全教育培训，从校长到学生做到一体化培训，并要求领导有重视心，教师有责任心，学生有警惕心，杜绝学生的不安全行为，树立学生的安全意识；同时，还要普及应急救援知识，做到遇事不慌，能够迅速有序地撤离，做到能够辨识危险、规避危险，保证在紧急情况下学生能够自救。

(4) 学校要建立完善的应急救援制度，组织以领导教师为核心的应急救援队伍，编制切实、可行的应急预案，并定期开展应急演练。

(5) 学校要完善日常安全管理制度，合理规划班级人员数量，做到师资安全双保险。此外，还要合理管理时间点，实行差时管理，尽量避免出现人群大规模集中。

5 结 语

本文以中小学校园踩踏事件为研究对象，将事故树与层次分析法相结合，构建了事故树-层次分析模型，对中小学校园踩踏事件进行了定量评价与分析，得出以下结论：

(1) 本文运用事故树分析法对中小学校园踩踏事件发生的原因进行了深入分析与识别，识别出导致中小学校园踩踏事件发生的主要影响因素，并归纳为硬件设施不足、不安全行为、安全意识不足、安全管理制度不健全、意外事件5个影响因素。

(2) 针对在事故树基本事件发生概率不明确的情况下事故树定量分析不准确的缺点，本文引入层次分析法，将事故树模型转化为层次分析模型，并进行定量分析，得到楼梯设计不合理、通道堆放杂物、恶作剧、楼道设计不合理、栏杆不牢固5个主要影响因素。

(3) 本文通过事故树由果找因的方法，得到了较为全面的导致中小学校园踩踏事件发生的原因，并运用层次分析法弥补了事故树在某些情况下无法定量化的缺点。通过利用事故树-层次分析法对中小学校园踩踏事件进行定量评价，得到的评价结果与实际情况相吻合，证明该方法在踩踏事件防控领域具有较高的应用价值。

通讯作者：刘 春(1972—)，男，博士，副教授，主要从事安全生产技术与管理方面的研究。E-mail：liuchun369@126.com