思维可视化：学生数学思维生长的助推器

马花

【摘要】发展学生的数学思维，是数学教学的根本任务。借助加工素材、问题驱动和深度对话，可以唤醒教材的思维可能，激活思维的内在动力和引领思维的纵深发展，让思维真正生成。教师可以让学生通过画下来、动手做、说出来等方式，让思维可视化成为学生思维生长的助推器，促进学生思维有条理、更灵活和系统化。

【关键词】思维可视化；画图；操作；表达

古人云：“人过留名，雁过留声。”在数学学习中，教师能否让学生的数学思维“思过留痕”呢？即学生在课堂上对数学知识结构及对数学问题解决方法进行有效表达，可以文字表达（数学情境描述）、图示表达（思维图示或数学图形）、式子表达（公式、算式、方程式、函数式等），这样就可以留下思考的痕迹。这样既利于学生自我反思、自我评价、自我改进和自我提升，也利于學生与其他同学的交流共享和思维碰撞，更利于教师及时采取有效措施进行有针对性的教学。实践证明，“思维可视化”是可以提升学生数学思维品质的有效策略，也是教师进行因材施教的有效方法。

一、让思维真正生成——思维可视化的基本前提

如果没有思维的生成，何谈思维的可视化？数学是思维的体操，也是思维的产物，但数学一旦以思维产物的形式固化下来，成为数学学习的对象时，它的存在，却未必一定能引发学生的思维。传统的填鸭式教学模式和机械训练模式急功近利，直奔结果而忽略过程，教师传输知识的过程就是生塞硬灌，学生学习的过程中就是生吞硬咽，这样不但违背了大脑的认知规律，而且还使学生产生了强烈的厌学情绪。

1.加工素材，唤醒教材的思维可能

我们都知道好的数学素材一定具有引发思维的可能性。那如何将可能性转换为现实，从而引发学生的有效思维呢？我们需要对素材进行精准加工，以适应儿童心理规律与年龄特点。

例如，苏教版三下《年、月、日》一课中，平年、闰年的知识是本节课教学的一个难点，如果教师仅仅出示几个年份，让学生算一算，然后告知平年和闰年的概念，从而视为数学上的一种认为规定，那么，其所内涵的思维空间便会被压缩。稍作调整，我们不妨给学生呈现如下学习素材：电脑软件“万年历”的演示，直观、形象令学生信服；课后阅读“小知识”作为补充，让学生明白为什么会出现每4年里有3个平年，1个闰年。这样一方面可以开拓学生的眼界，激发学生课下进一步探究的欲望，另一方面也唤醒了素材的思维可能，让素材真正成为思维的引擎。

2.问题驱动，激活思维的内在动力

好的数学问题能引发学生的思维。这些问题应具有更大的思维空间，能引发学生的思维冲突，激活思维的内在动力。

例如，苏教版教材二下《三位数加法》之后，特地安排了“加法估算”这一内容。在教学中，教师不应把估算方法直接告诉学生，而应利用学生已有知识，提出新的问题：“估计一下，买一部电话机和一个电饭煲，大约需要多少元？”“任意选购两件商品，估计大约需要多少元？”等实际问题。此时，倘若教师能够引导学生边思考、边体会，他们或许会在解题过程中自觉地想到估算。

又如，苏教版教材三上《整十、整百数乘一位数的口算和估算》教学中，教师创设了小猴兄弟俩买水果的情境。

师：从这幅图中你知道了哪些信息？

生：西瓜每箱48元，哈密瓜每箱62元，它俩带了200元。

师：200元买4箱西瓜够不够呢？你需要先知道什么？

生：我需要知道4箱西瓜多少元？列式是48×4。

师：你能不计算出48×4的准确结果就解决这个问题吗？

生：是不是可以用估算的办法？（众生思考）

师：可以试试看呀，把你准备怎么估算的思考过程写在作业纸上……

估算是解决实际问题的常用算法。为凸显它的应用价值，教师创设了一个可以估算的购物情境，在“带200元买4箱西瓜够不够”问题的引领下，学生依据之前的学习经验进行思考，却发现还不会笔算“48×4”，只会口算“50×4”。在这样的认知冲突之下，教师不失时机地提出“你能不算出准确结果就能解决问题吗”的目标驱动，由此，学生产生估算需要，顺理成章地进入到估算情境中，这样思维也在问题驱动下得以充分激发与展开。

3.深度对话，引领思维的纵深发展

没有思维的碰撞就没有思维的迸射，没有对话就没有思维的砥砺。让学生由自己独立思考，形成自己的见解后，如何引导学生在分享与交流中建构意义，是推动学生思维向纵深发展的重要路径。

生3：我举个例子，8个人里的3个人，加上8个人里的2个人，得到8个人里的5个人。

……

此时，教师不必急于出面，而应将问题重新抛给学生——“刚才几位同学的发言，你印象最深的是什么？”引导学生展开对话，或在比较中发现差异，或在协商中寻求共识。其实，真正的思维正是在这样有深度、开放的对话过程中得以展开和深化的。

二、创新教学路径——让数学思维看得见

在教学中让学生思维能够看得见，就是支持学生实现自主探究式学习的一种非常有效的学习策略，运用这种策略就可以帮助学生在完成知识建构的过程中发展学生的心智水平，即实现核心素养的发展。我们需要调动学生的多重感官，参与到思维的产出、发展与表达过程中来。在运用思维可视化建构知识的过程中，用直观的图形、符号展现思维的条理性，在动手实践中展现思维的灵活性，在语言表达中展现思维的系统性。

1.画下来，让思维条理性展现

思维是人脑对客观事物的本质属性和内在规律间接的、概括的反映。它是人类所具有的高级认识活动，是对新输入信息与脑内储存知识经验进行一系列复杂的心智操作过程。实践证明，化抽象为直观，即把直观的数学画出可视化的直观图，为学生的思维提供一个形象化的支撑，将内隐的难以言传的数学思维过程和方法个性化地呈现出来。

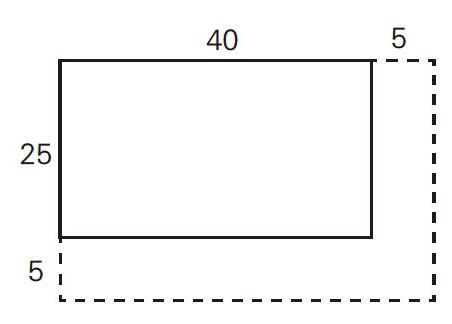
例如，苏教版四下《解决问题的策略》，有这样的一题：一个长方形菜地长40米，宽 25米，现因扩建，长和宽同时增加5米，增加的面积是多少平方米？教师引导学生用直观图把题意画出来。

有了直观图的依托，学生很容易想到用大面积减去小面积的方法求出增加的面积这种常规解法——[40+5×（25+5）] -40×25。如果教学到此结束，显然是不够的，习题的作用并没有得到充分开发。这时教师可以抛出一个问题，从而转化学生的思维路径：这道题除了用大面积减去小面积的方法解决，还可以用怎样的方法呢？能不能想办法直接求出增加的面积呢？于是就有了以下不同的方法：

生1：把增加部分的面积分成了①、②、③三块，如下图：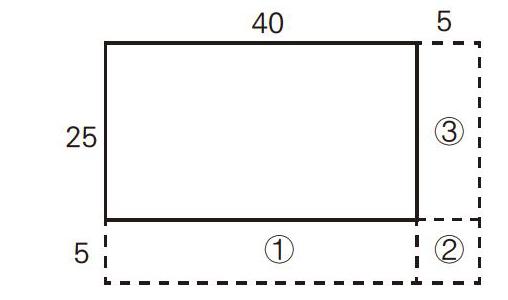

生2：把增加部分的面积分成了①、②两块，如下图：

生3受直观图的启发，直接把分成的①、②两块拼成了一个长方形，如下图：

小小的示意图为学生的思维打开了一条绿色通道，一方面外化并反映出学生不同的思维方法、路径和水平，另一方面给教师了解学生现状，进而改进教学方式做出有针对性的引导提供了可靠的技术保障。

2.动手“做”，让思维灵活展现

数学思维不是孤立的，它往往伴随着具体的数学活动展开。由于小学生的思维水平正处在具体运算阶段，所以在教学时，教师可以通过引导学生动手“做”数学，在操作、演示、实践过程中，“观察”学生的思维路径与现状，灵活调整自己的教学，从而更好地培养和发展学生的数学思维。

在教学苏教版一下《100以内数的加法》时，我给学生准备了15根小棒，要求学生用小棒表示出35。很显然，这个操作具有一定的难度，学生的第一个反应就是小棒不够，怎么能摆呢？但很快就有一些反应较快的学生想出了办法：

生1：可以将几个人的小棒放在一起摆出3个一捆的是30，5个一根的是5，加起来就是35。

生2：可以将一支铅笔当作10，只需要摆3根铅笔，然后再拿5根小棒，就摆出了35。

接下来便有更多的想法呈现出来。此时他们的思维显然已經超越了一年级学生的应有水平，学生不知不觉学会了替换思维，这朴素的方法蕴含着对应和假设的思维萌芽，教师顺势可以组织学生进行比较，在沟通、对比中寻找最好的表达方式，并在互相学习的过程中提升自己的理解、认识与思维水平，为下一步数学探究打开了广阔的空间。

3.说出来——让思维系统化展现

语言是思维的外壳，借助语言我们可以让思维展现出来。但在教学中，教师应该要克制自己说的欲望，尽可能给学生创设更多表达的机会，这样学生能够在对话、沟通、质疑和讨论中展现、发展和提升思维。

在苏教版二下中，学生认识钟面的时间是一个难点，很容易认错。尤其是接近整时或者超过整时一点的，错误率极高。如写出下图钟面上的时间，学生就会出现如下错误结果：10：11、9：11、10：55、11：10、11：55。分析原因，11：10、11：55是没分清时针和分针导致的错误，而10：11、9：11、10：55则是没弄懂时针和分针行走的规律导致的错误。仔细分析这些错误，让学生说说相应的思考过程：先找钟面上较短的时针，时针走过几，就是几时多；再找钟面上较长的分针，指向几，走了几×5分钟，因此，钟面上的时间是几时几分。上面的钟面比较特殊，时针不容易判断时，我们就先观察分针有没有走过12。没有走过，那说明时针还没有到整时；如果走过了12，那说明时针走过了整时。

学生像这样进行数学思维，并经常说一说主要思维过程，就会发现和避免以上出现的各种错误。透过学生的语言表达，我们不难发现，每一种表达的背后，都隐含着某一种思路。这些，都给教师触摸学生的思维轨迹创造了极佳的条件。

由此可见，思维可视化作为学生数学思维生长的助推器和重要学习策略，可以有效促进学生数学思维的条理性、灵活性和系统化，不断提升学生数学思维品质，避免和减少各种数学作业错误，提高数学成绩。思维可视化作为教师了解学生、读懂学生和研究学生并进行因材施教的重要教学策略，具有丰富的教育意蕴和实践价值，值得一线数学教师深入探讨和研究。

【参考文献】

[1]教育部基础教育课程教材专家工作委员会.义务教育数学课程标准（2011年版）解读[M]. 北京：北京师范大学出版社，2012.

[2]张齐华. “思维可视化”视域下小学数学课堂之重建[J]. 江苏教育：小学教学，2017（04）：48-50.

[3]刘丽娟. 让儿童的思维看得见[J]. 人民教育，2014（23）：40-42.

[4]夏忠. 画数学，为学生提供可视化的思维路径[J].教学与管理，2017（04）：47-49.