基于结构熵权法的非侵入式家电识别研究*

许仪勋，王洪安，李旺，陆青

(1．上海电力学院，上海200090;2．国网临沂供电公司，山东临沂276000)

0 引言

在智能用电发展过程中，负荷识别发挥着重要作用。自上个世纪80年代，麻省理工学院学者George W．Hart［1］提出了非侵入式负荷监测(Nonintrusive Load Monitoring，简称NILM)技术，即只需在居民用户的电力入口处安装硬件装置，便可实时监测和分析用户的用电信息。通过非侵入式居民负荷识别技术的应用，居民用户可以直观地了解各个家用电器的具体电能消耗情况，从而使得居民的用电计划更加具有合理性，家用电器的选择更具有针对性，以达到降低电能损耗，减少居民家庭的用电费用，提高居民节能环保意识的目标［2］。

非侵入式负荷识别的核心是负荷特征的提取和识别算法。目前研究识别算法的比较多，由单一算法到多种算法相结合，但负荷特征基本选择的比较单一，比如有功功率［3］、暂态开关状态［4-6］、稳态谐波特征［7-10］等，由于电压和电流波动等因素干扰，单一特征所得到的识别结果可能会与实际用电情况不一致，以有功功率为例，在文献［11］中通过单一特征有功功率进行分析，最终在2个功率比较接近的电器中，无法进行正确的识别。

随着智能小区的不断建设和发展，积累了大量的基础用电数据，数据中隐藏着用户的用电行为习惯，对这些用电数据进行挖掘研究分析，可以得到用户的用电行为习惯。近年来，已有一些学者对这些数据进行研究分析，但基本针对于电力用户分类，如文献［12］以传统行业划分为基础，提出基于聚类的用户分类研究;文献［13］提出从当前市场价值、潜在市场价值、区域贡献价值等方面对用户进行分类研究，建议对不同类型用户制定不同的营销策略。

熵权法是一种客观的赋权算法，相对于主观赋权法，精度较高，客观性更强，能更好的解释所得到的结果，而且可以用于任何需要确定权重的过程，也可以结合一些方法共同使用，所以选择熵权法来确定各特征属性的权重。

基于上述所述，首先，提出采用家用电器的多种参数特征来进行电气负荷识别;然后，通过对居民用电数据分析，归纳居民用电行为规律，并创新性的将其作为电气负荷识别的判据之一;最后，提出结构熵权法，即熵权法确定有功功率、无功功率、谐波电流和居民用电行为所占权重，主观赋值法对识别结果进行赋值，然后将权重和赋值相结合，计算出最终的权值，进而确定出电器开启结果。通过实验验证，此方法可以提高负荷识别的准确率。

1 居民用电行为研究

REDD数据是由麻省理工学院建立的能源分解参考数据库，REDD数据库中数据都是采用UTC(U-niversal Time Coordinated)时间戳来进行记录的，通过UTC时间转换器将其转换成对应的日期和时间，并对家庭5一周内采集数据进行分析，来获取各个时间段案例中用到的各电器的使用情况，作为居民用电行为的依据，如表1所示，并选出其中一天的功率变化，如图1所示。

表1 家庭5用电行为分析表Tab．1 Electricity Behavior of family 5

图1 家庭5某一天的功率变化图Fig．1 Power variation diagram of household 5 in one day2

2 家电负荷特征选取

2．1 有功功率

有功功率计算公式:

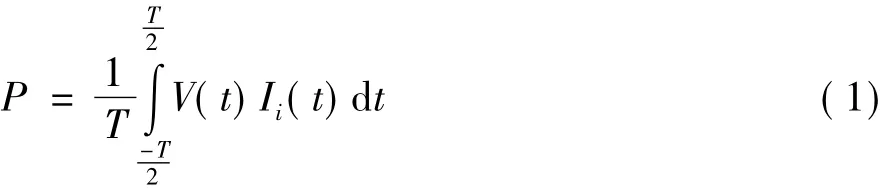
对电力负荷功耗进行分解优化目标函数:

式中Pi是数据库第i个设备的功率;P为当前的功率。

2．2 无功功率

无功功率计算公式:

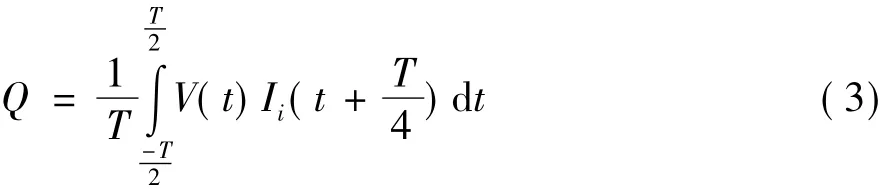
对电力负荷功耗进行分解优化目标函数:

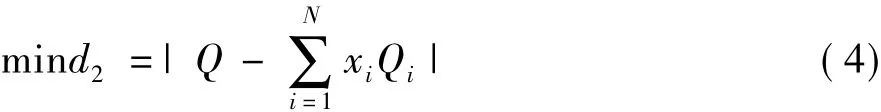
式中Qi是数据库第i个设备的功率;Q为当前的功率。

2．3 谐波电流特征

由文献［14］可选取谐波电流特征作为负荷识别的特征之一，具体如下:

IL=ISX (5)

式中IL为采集器采集到的家庭总电流;IS为家电设备模型参数矩阵;X为各家用电器的工作状态矩阵。因此，负荷识别问题转化为求解最优组合问题，取目标函数为:

通过负荷识别算法求得最优组合解，使得目标函数值f取得最小值，此时从X的对应元素值中即可获知各个家电负荷的工作状态，从而可以统计各个家电负荷的能耗信息。

3 结构熵权法的多特征负荷识别方法

为了更可靠地提升非侵入式电力负荷的分解能力，以及不同特征量对负荷识别准确度影响的大小，给出一种基于结构熵权法的多特征识别算法，其基本思想是将定量分析的熵权法和定性分析的主观赋值法相结合，确定最终权值，获得负荷识别结果。

信息熵本是用来刻画信息论中所包含信息的无序度的一个量，通过信息熵来度量信息的无序化程度，熵越大则无序化程度越高，相对应的该信息所占有的效用就越低。基于此原理，将信息熵用来确定负荷识别各特征属性的权重，通过采集数据形成数据序列，并计算该数据序列的信息熵，如果该数据序列的差异程度大，则该特征的影响程度越大，相应的就赋予其较大的权重，并通过数据序列的变异程度来确定各特征属性对负荷识别影响程度的大小。

在结构熵权法的多特征负荷识别中，采用离散粒子群算法实现目标函数寻优的目的，离散粒子群算法是由Eberhart博士和Kennedy博士于1997年率先提出的一种新型仿生种群智能优化算法，主要解决0－1规划问题，即每个粒子用一个二进制变量来表示，与其他进化算法相比，其最吸引人的特征是易于实现和更强的全局优化能力，其寻优过程如图2所示。

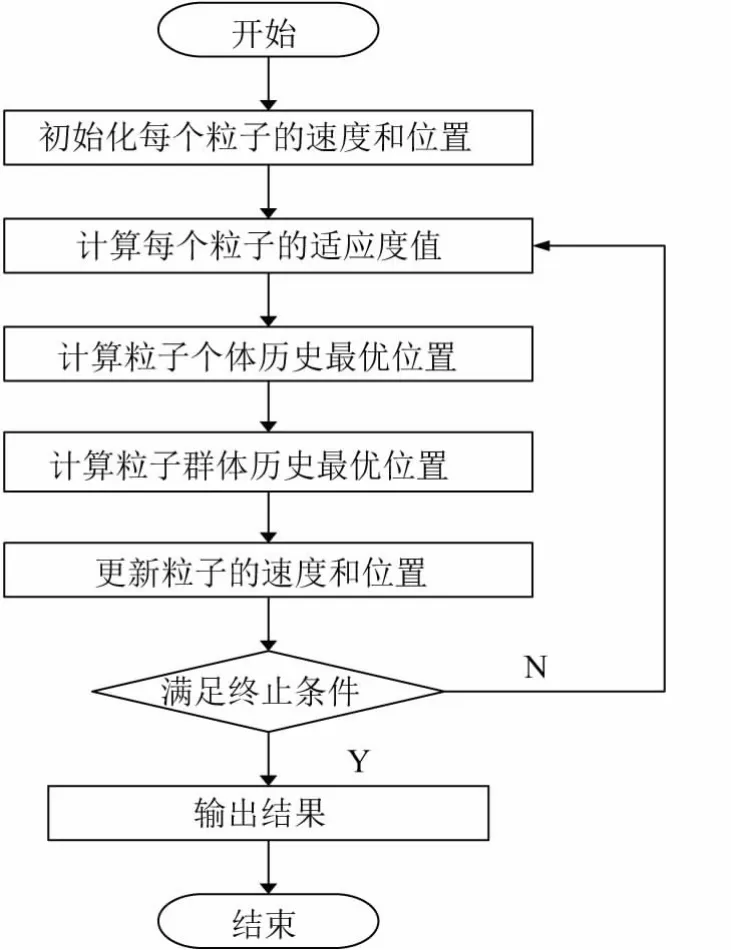
图2 离散粒子群寻优过程Fig．2 Discrete particle swarm optimization process

基于结构熵权法的多特征负荷识别算法的具体计算步骤如下:

(1)数据采集和处理。熵权法的权重计算需要构建属性决策矩阵，而属性决策矩阵的构建需要原始数据的支持。本文原始数据的获得由离散粒子群算法分别对有功功率、无功功率以及谐波电流特征的目标函数进行寻优，获得电器状态组合和目标函数的适应度值。首先，将有功功率、无功功率、谐波电流特征和居民用电行为概率作为属性，将其表述为xj;其次，把各个识别结果的开关状态组合作为方案，将其表述为Am;最后，将适应度值作为原始数据，将其表述为xij，形成属性决策矩阵:

对原始数据xij进行归一化处理，计算比重Fij:

(2)熵值计算。针对第j个属性，利用该属性下的数据列计算该属性的熵值Ej:

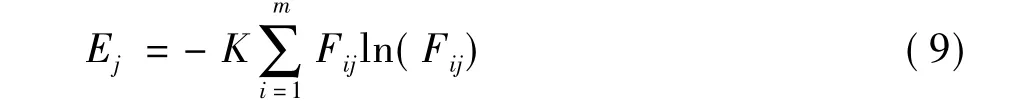
式中常数K=1/ln(m);m为方案数，即保证0≤Ej≤1。

(3)计算偏差度。计算第j个属性的偏差度dj，对于确定的第j个属性，如果该属性对负荷识别影响程度越小，则其该属性下的数据列越接近完全无序状态，Ej越大，该影响因素的偏差度应越小，因此定义:

dj=1－Ej(10)

(4)计算权重。对以上计算出的偏差度进行归一化后得到的数值即为每个属性的权重，它反映了该属性对负荷识别的影响程度的大小。其中第j个影响因素的权重计算公式:

(5)形成识别矩阵。把各个电器特征的电器识别结果的开关状态组合按照式(12)的矩阵形式排列:

Dn=［Di(1)Di(2)Di(3) ．．．Di(z)］，i=1，2，3…，n，其中，n为电器特征数目;m为每种特征所选出的结果数目。

(6)对识别矩阵赋值。给每个Di(j)(i=1，2，3…n;j=1，2，3…m)赋权值 Wi，依据相似性将 Di(1)的加权值设定为m，Di(2)的加权值设定为m－1，依次递减后Di(m)为1，有:

Wi(j)=m+1－i (13)

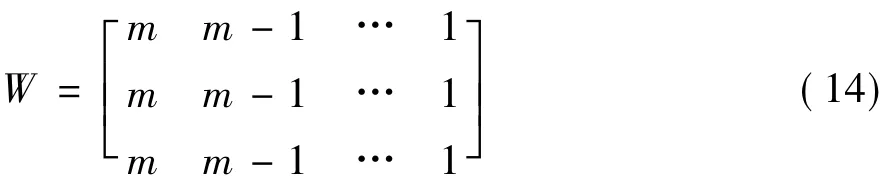
Di(j)的加权值为W中对应矩阵位置上的加权数。

(7)将熵值法确定的权重和对识别矩阵的赋值结合。将各行中出现的元素，与其相对应的赋值和权重相乘得到权值，并将相同的元素的权值求和，权值最大的就是判定的电器组合类型。

4 算法验证

为了验证居民用电行为对负荷识别具有重要的作用，采用由麻省理工学院建立的能源分解参考数据库进行实例仿真。对家庭5中火线2上的主要家电负荷的功率进行获取以及对其进行频谱分析，利用MATLAB进行编程，从中提取出基波分量和谐波分量，具体的家电负荷特征参数值如表2和表3所示。

表2 家庭5火线2上主要家用电器有功和无功功率Tab．2 Active and reactive power of major home appliances of household 5 wire 2

从表3中可以看出，家庭5中火线2上有8种主要家电负荷，共有11种不同工作状态。为了验证结构熵权法具有较高的负荷识别准确率，与单独使用有功功率、无功功率和电流谐波特征做比较。采用离散粒子群来进行寻优，令迭代次数为100次，种群规模为40，学习因子取值为1．49;图3～图5分别为电冰箱状态一与家电四状态二同时工作时，有功功率、电流谐波特征和无功功率的PSO算法的收敛性。

由图3可以看出，PSO迭代4次就进入稳定，得到的结果为电冰箱状态一、家电四状态二在运行与实际情况设备状态开启一致，图4为PSO迭代15次后进入稳定，得到的结果为电冰箱状态一、家电四状态二在运行与实际情况设备状态开启一致;图5为PSO迭代2次后进入稳定，得到的结果为电冰箱状态一、家电四状态二在运行与实际情况设备状态开启一致。对该例进行40次试验，有功功率识别准确率为22．5%，无功功率识别准确率为32．5%，电流谐波特征识别准确率为48%，有功+无功+谐波电流的识别准确率为57．5%，结构熵权法识别准确率为77．5%。为了进一步深入对比文中方法算法和单一特征的识别准确率，现对不同家电负荷分别进行实验，对多种家电工作状况试验各设置运行40次，并统计分析了本方法和单一特征识别出的次数和准确率，详细数据如表4所示。

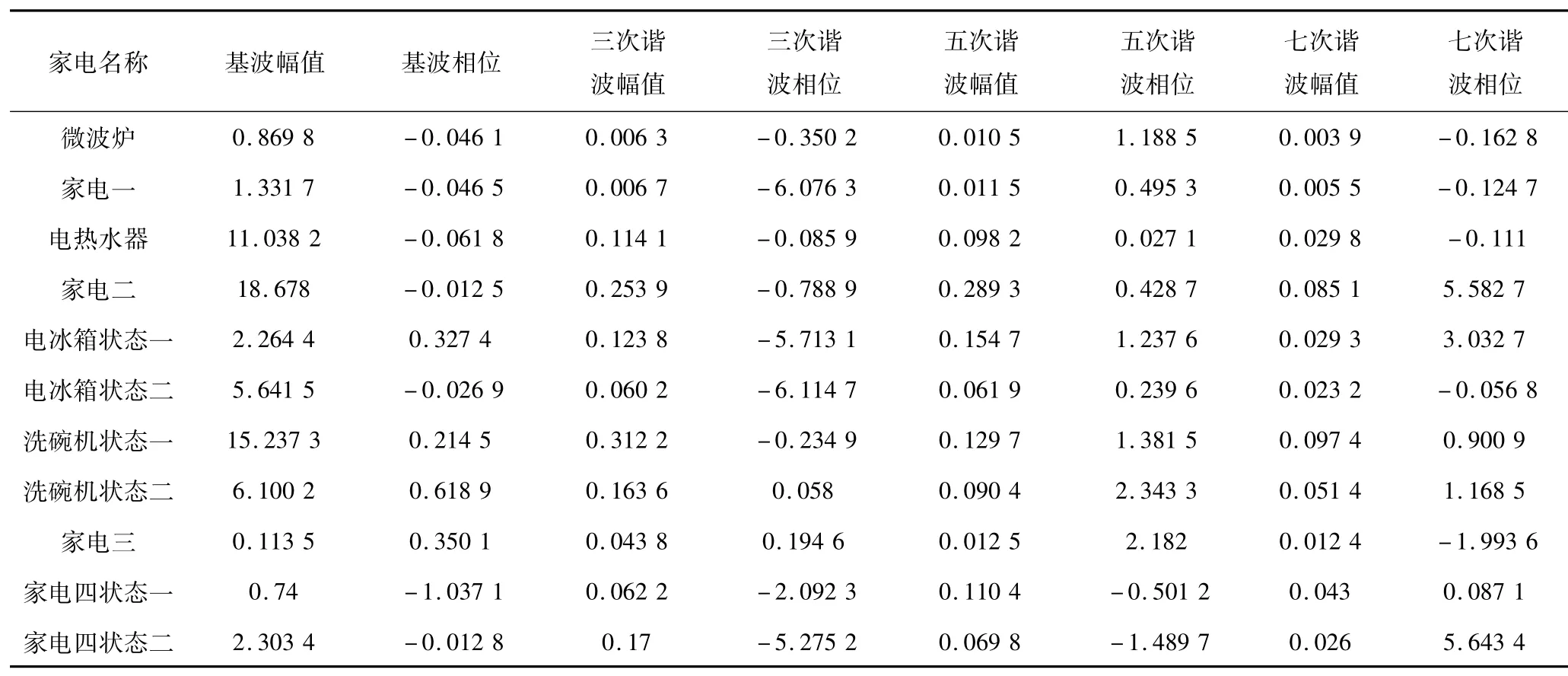
表3 家庭5火线2上主要家用电器特征量Tab．3 Characteristics of major home appliances of household 5 wire 2

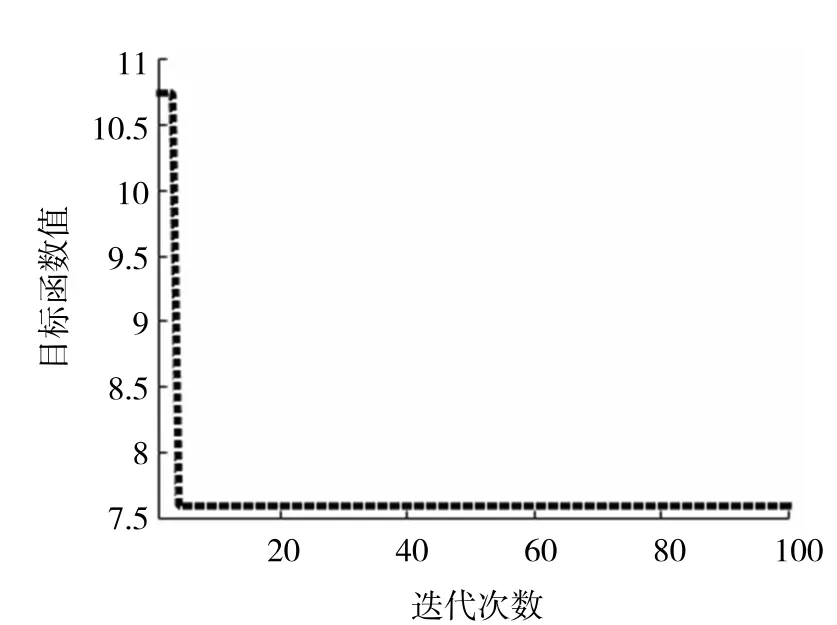
图3 PSO算法的收敛性(有功功率)Fig．3 Convergence of PSO algorithm(active power)

图4 PSO算法的收敛性(电流谐波特征)Fig．4 Convergence of PSO algorithm(current harmonic characteristics)

图5 PSO算法的收敛性(无功功率)Fig．5 Convergence of PSO algorithm(reactive power)

从表4中的数据可以看出，有功功率识别的平均准确率为31．25%，电流谐波特征的平均识别准确率为48．875%，无功功率识别的平均准确率为34．375%，有功+无功+谐波电流的平均识别准确率为61．875，而结构熵权法的平均识别准确率为78．75%，多特征明显高于单一特征的识别准确率，且考虑居民用电行为的准确率更高，因此，考虑居民用电行为的结构熵权法可以有效地提高负荷识别准确率。

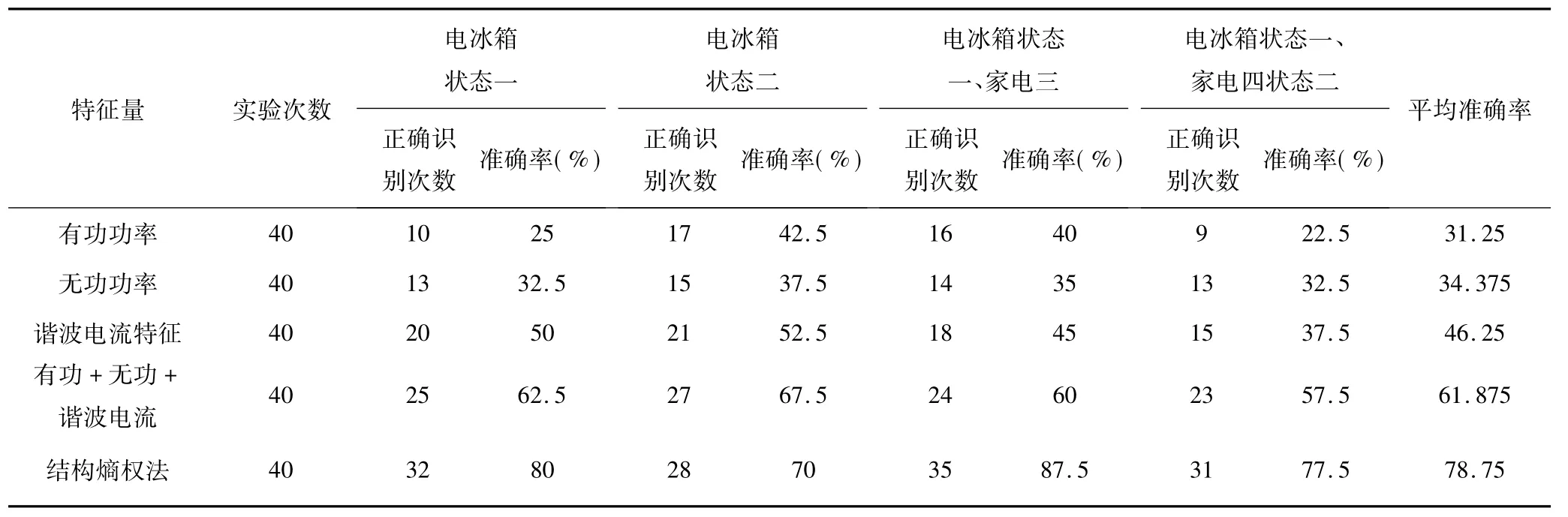
表4 家庭5负荷识别准确率Tab．4 Household 5 load recognition accuracy rate

5 结束语

为了提高电力负荷分解性能，提出了利用多个特征量进行识别，并创新性地将居民用电行为作为一种特征去识别电器负荷。利用熵值法来去确定每个特征的权重，然后根据赋值法对各方案赋值，通过赋值和权重最终确定识别结果。通过实验验证，该方法可以有效提高电器识别的准确率。下一步，将会针对多状态电器进行深入研究，更进一步提高用户用电体验。