基于BP神经网络的交通流量预测算法
吴志光
(池州职业技术学院 机电系,安徽池州247000)
先进的交通管理系统和交通控制系统都需要实时和准确的交通流量信息,因此为智能交通系统提供一个精确的交通流量实时预测一直是研究热点,各种算法井喷涌出,但还处在一个发展时期,在理论和应用上都不够完善。本文是将神经网络技术研究与交通信息预测研究紧密结合,在总结国内外研究成果的基础上,改进网络结构,合理的改进算法来提高预测准确度,提出了一种基于BP神经网络算法的交通流量预测模型,并分析系统的稳定性和进行了仿真实验。通过对比预测结果表明,本交通流量预测系统具有很强的自学习、自组织、较强的容错性等特点,能很好地解决具有随机性、模糊性、动态性和不确定性的非结构化的交通流量预测这样一个复杂系统。
1 交通流量系统
1.1 交通流量的参数
交通流量的参数基本上分为三个方面:流量、速度、通过率。它们是在某个特定时间内道路的特定地点、车道通过的具体数,其中包括机动车、非机动车、人流量。但是本文研究的是机动车流量.交通流量的参数为随机数,即在不同的时间,不同的地域都是随机的,随着时间、天气、环境变化所影响。所以在进行研究这些参数变化时,要进行合理的交通规划和措施[2]。
流量指的是在某个特定的时间内,通过这一地点或者某条车道的交通数,这其中包括机动车流量、非机动车流量、人流量等,本文中就是机动车流量,并且是两个方向以上的车辆个数。速度,在特定的时间内通过这一地点的速度。通过率是指某一特定时间内,有多少车辆通过这一地点。通常情况下,这三个参数都是随机的.
1.2 交通流量的诱导系统(GPS)[2]
交通诱导系统(GPS)的使用是进行城市交通预测的重要研究内容之一,它能让驾驶人员在当前位置能选择到达目的地的最优路径,并且在行驶途中,遇到的交通红绿灯少,人和车流量少,并且有效地减少交通阻塞。实现了交通网络分配的最优路径。但是引入交通诱导系统(GPS)必然会引发驾驶人员交通行径路线的变化,同时也改变了交通控制参数,但是(GPS)研究起步晚,各方面技术并未达到成熟,在城市交通预测中没有达到预测效果.
交通流量的特征预测,是指通过在某一特定时间内的数据做出预报[2]。一般来说交通流量参数预测可以分成为两大类:时间序列预测和综合预测。前一种模型简单,预测难度大,预测误差大,不够准确。一般采用后一种。图1为交通诱导系统的基本功能:

图1 交通流量框架图
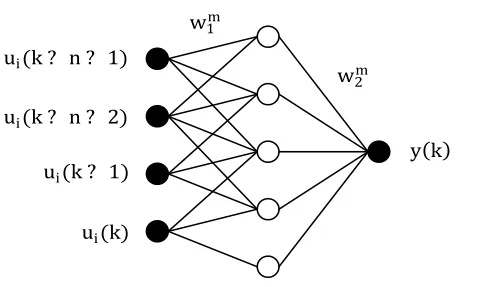
图2 神经网络结构图
不同时间的同一地点交通流量参数也变化,合理科学的研究交通流量的参数有利于帮助交通规划、管理、设计和交通的安全具有重大意义。特别在交通改善方案时,也需要进行也需要进行交通流量的特征预测,并通过在某一时间的数据做出预报。
2 基于BP神经网络的交通流量预测
2.1 基于动态控制理论的神经网络建模
本文利用i路段的前n时段的交通流量值来预测下一时段的交通流量值。令[][ui(k)][ui(k)]表示该路段在k时间的交通流量的真实值。建立的网络模型如图2所示,其中[uik-n-1][uik-n-1][uk][uk][uik-n,uik-n+1,uik][uik-n,uik-n+1,uik]作为为外部输入信号,[wm1][wm1]为输入层与隐含的层的连接权矩阵,[wm2][wm2]为隐含层到输出层的连接权矩阵,[yk][yk]作为输出值。
隐含层各单元的输入为:
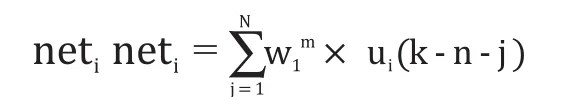
设隐含层的传递函数为:f(x)
得出隐含层的输出如下:
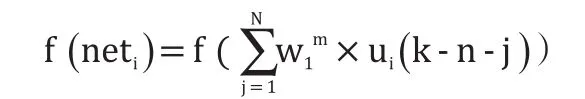
2.2 基于最小梯度的神经网络学习优化
本文中神经网络的模型建立,假设只有一个隐含层。对于第j个隐含层节点,它的总输入为表示第i个输入节点到第j个隐节点的连接权系数。对于该节点,它的输出为输入层到隐含层的连接权矩阵。
根据梯度下降算法,为了减小误差,必须对输入层到隐含层的连接权系数进行调整。
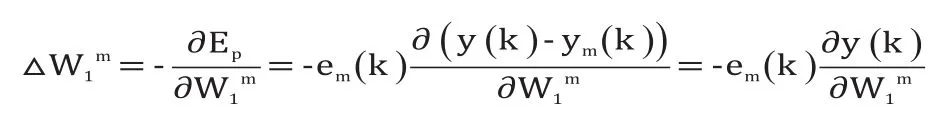
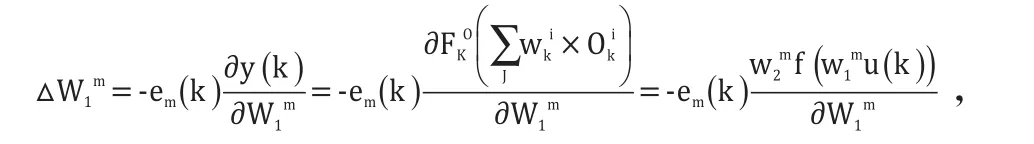
则权值变化为:
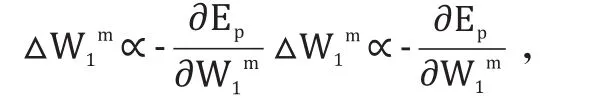
采用一种改进的算法。其权值调整如

假设神经网络预测的模型是稳定的构造建模误差em(k)em(k)的李雅普诺夫函数,如果给定的函数趋向某一特定的稳定值,则系统的输出跟预测的希望基本一致,则必须
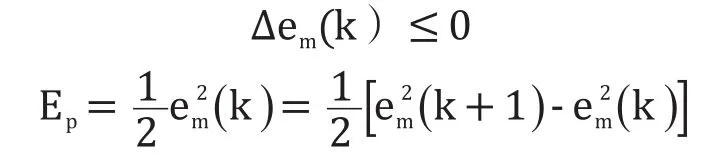
2.3 基于动量的改进BP算法
BP神经网络的算法缺点在于学习效率低、收敛速度慢、很难确定隐层和隐节点个数,并且随着学习维数的逐步增加,网络的性能可能会越来越差,预测越来越不准确。其次BP神经网络对参数和权值的训练更为敏感,网络初始值的选取和隐层节点个数的确定影响网络的准确度和精度。在梯度下降算法中权值的选取和阈值的大小与网络的误差的一阶导数成正比关系。根据此类梯度下降算法,如果网络初始值确定,就确定了网络的收敛方向[6]。因此一开始对权值选择和阈值就变得重要。为了加快BP网络算法学习速度,避免陷入局部最小值,本文采用附加动量法来改进BP算法,加入的动量实质上相当于阻尼项,有助于系统滑过局部极小值,减小了学习过程的振荡趋势,改善了收敛性,提高训练速度。
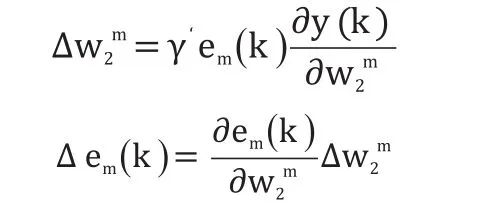
所以得到:
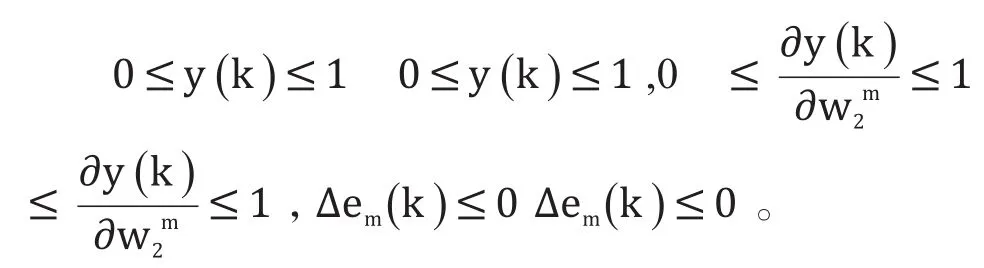
3 系统仿真实验
3.1 系统仿真图
对交通流量的预测可以分为三种不同的类型:晴天、阴雨天、暴雨天、仿真数据选取分别取自三种天气的同一路段的不同时刻的同一时间进行仿真,本文选取的是阴雨天进行仿真。选取其中的100组数据,70组进行训练,15组验证,15组进行测试。如果训练数据和验证数据将网络训练的好,那测试数据将很好的预测,这些数据可以得出预测值与真实值之间的比较。本文所用的神经网络为前馈向BP神经网络,需要在仿真过程中对神经网络的结构和权系数进行调整。
3.2 实验效果仿真图
对已经选取的数据进行训练和测试,只有一个隐含层,初步选取隐含层的节点数量为10个,如果网络的非线性程度强,可以适当增加隐含层的节点个数,来确保系统的稳定性和减少实验的误差,通常情况下网络的训练好坏与两个参数息息相关,一个是自相关误差。第二个是系统输出误差。
图3为系统自相关误差图,如果假设系统是没有误差,即模型在一个时间的输出误差跟另一个时间段内的输出误差无关,这种模型在实际情况中很难实现。定义在10%左右之间的误差是被接受的。
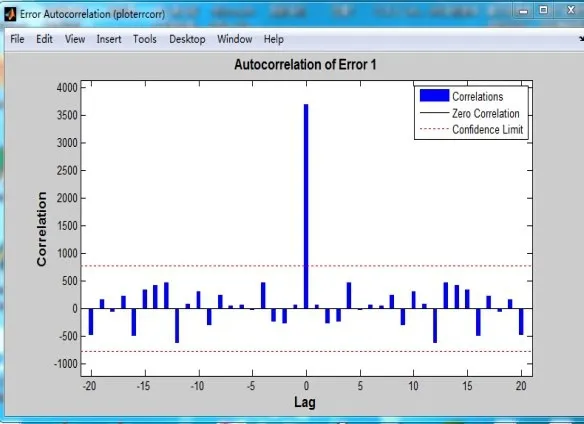
图3 神经网络误差分析图
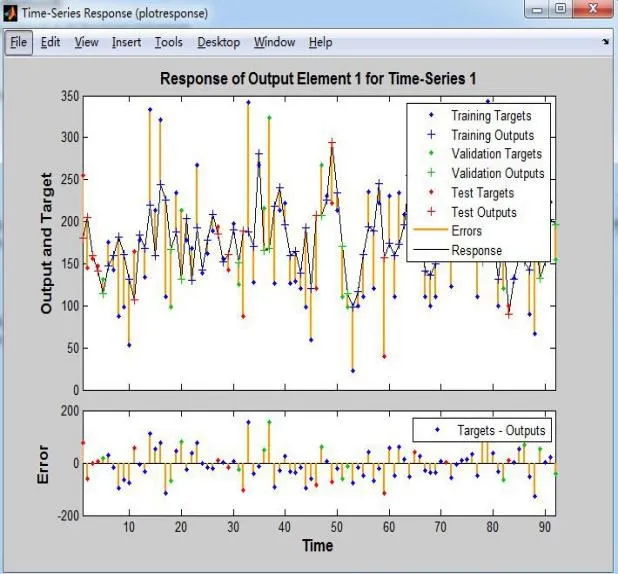
图4 真实值与预测值对比图
3.3 真实值与预测值的比较
经过多次实验学习,该网络有了很好的拟合效果,从仿真图形可知,晴天,阴雨天,暴雨天不同时间段的差异,在进行数据训练,测试,验证中,网络的权数是随机给定的,训练是多次的,保证自相关误差是越小越好。
4 结束语
本文通过在智能控制领域内对交通流量预测的一个实验,针对这样一个具有随机性、模糊性、动态性和不确定性的非结构化的一个复杂系统,提出了基于BP神经网络建立模型进行仿真,取得了较为理想的效果,但存在问题也比较多,比如网络的收敛速度慢,随机性强,也存在着隐含层数目和节点数目选择的问题,只有通过试凑法来最终确定。应用神经网络对交通流量的评估存在一定的误差性。但是总体效果不错。并且在其他方面应用也很广泛。
神经网络作为一种智能信息处理的技术,根据内在的联系建立模型,具有优良的非线性逼近能力和对复杂信息综合处理的能力,根据神经网络的这一特点,不需要建立非线性系系统和数学模型,在未来,基于神经网络领域的预测方法仍将是主要研究方向。

