滴灌系统在边坡人工再造植被灌溉中的应用及设计参数优化研究

石中勇

（中煤地质工程有限公司北京水工环地质勘查院，北京100040）

0 引言

随着生态文明建设的提高，矿山环境修复、公路铁路沿线创面修复大量展开，在北方季风性半干旱区，灌溉是保证坡面再造植被生长发育所需水分的主要手段之一，对边坡尤其是岩质边坡人工再造的植被来讲，初期的人工养护是关键中的关键。由于边坡上土层或基质较薄，含蓄水能力有限，因此选择适宜的灌水方式，不仅可以使有限的水资源得到合理高效利用，还可以使植被尽快成坪，从而有效减少水土流失[1]。喷灌及滴灌技术已经应用成熟，但对于边坡条件下，这种问题往往解决的不是很好。较高较陡的边坡上，喷灌的水会沿着边坡快速流动，导致面流过大渗入量不足，同时冲刷损毁坡面。传统滴灌虽能减缓，但由于人造地形附近水源地水质往往较差，水中杂质较多，极容易堵塞传统滴灌用管的滴水孔，而且传统滴灌用管都是统一设计外形，边坡地形特点导致传统滴灌系统对人造土壤的灌溉能力分布不均匀，会导致部分植被生长困难，从而使边坡地形失去意义，因而无法良好解决均匀灌溉和高效利用水资源的问题[2,3]。

本文根据传统滴灌系统的设计，针对传统滴灌系统存在易堵塞灌水孔道、无法控制不同高程下灌溉均匀性等特征，设计一种可以应用于边坡地形中的滴灌系统，并对该滴灌系统的设计参数进行分析，计算讨论不同边坡地形下如何设计系统参数，使滴灌系统尽量保证对边坡地形的灌溉能力均匀的情况下尽量节约水资源。

1 滴灌系统灌溉水流动物理模型

本文设计的滴灌系统包括泵水装置、水源传递管路、低位储水池、高位储水池和滴灌装置，其中最重要的功能体现在于滴灌装置中[4]。滴灌装置是一组由不同渗透能力的渗水管组成的成套系统，整套滴灌装置在不同位置的设计方式不同，进而在不同高程位置的边坡上能保证灌溉能力的均匀分布。渗水管外侧包裹了具有多孔特性的渗透层，这样使得渗水管在保证传统滴灌系统低耗水量的优质特性的同时，发生渗水孔被杂质堵塞的概率大大降低；进而根据渗水管所需要灌溉覆盖的高程位置，使用不同渗透系数的渗水材料，从而根据实际坡度需求对滴灌系统的排布设计进行合理分配，使边坡地形在灌溉过程中实现高效的水资源利用。本滴灌系统设计使得复杂边坡地形也能实现均匀灌溉，避免了由于不均匀灌溉所导致植被按非预期模式生长，使边坡人造植被功能失效。图1为该滴灌系统设计功能部件示意图。

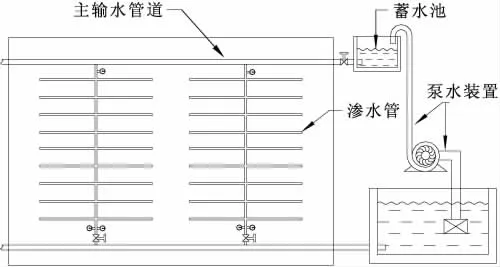
图1 滴灌系统设计示意图

泵水装置用于对整体系统的动力提升，将附近水源地的水资源运移到边坡地形的高处，使水源产生了重力势能，通过势能驱动灌溉用水运移，达到灌溉的目的。各种输水管路水资源分配给渗流系统的终端。渗水管是整个滴灌系统的灌溉终端，负责将水源直接灌溉到种植层内部。

图2为渗水管位置的微观结构设计图。如图2所示，渗水管包括支撑硬管、渗流层和出水孔，渗流层包裹在支撑硬管上，并覆盖出水孔。

图2 渗水管处微观结构示意图

根据图2，可以很直观地看到，实际上渗透层的渗透系数是整个灌溉系统的关键设计参数。

2 滴灌系统灌溉水流动数学模型

由于本灌溉装置设计是根据边坡地形对渗水管的表面包裹渗透层的渗透系数进行修改，进而实现其灌溉能力的均匀性，故每排水平方向的渗水管表面包裹渗流层渗透系数都会不同，所以设计时应根据实际灌溉需要对渗透系数进行设计定义[5,6]。滴灌装置设计是根据边坡地形而来，而边坡地形直接会决定该滴灌系统的渗透系数，则渗流层渗透系数的计算应由边坡地形实际需求出发。

首先确定该边坡每日所需供水量Q(m3/h)，假设该边坡地形平整，坡度固定，并在该边坡上已埋设n排渗水管，则可以根据下列公式得到所需供水量Q与单根渗水管表面覆盖层内灌溉用水渗透速度Vi(m/h)之前的关系式：

其中，i为渗水管的排数，i=1,2,3,…,n；L(m)为渗水管中支撑硬管的设计长度；D(m)为渗水管中支撑硬管的设计直径。

为确保整个边坡上的灌溉用水比较均匀，应保证n排渗水管上发生渗流速度Vi都是相同的，即V1=V2=…=Vn。水力达西公式在该滴灌系统中可表述为：

其中，ki为第i排渗水管渗流层的平均渗透系数 (m/d)；Pi为第i排渗水管内压力(Pa)；P0为渗水管渗流层外侧压力(Pa)，即大气压，由于设计以大气压为基准，故P0=0；γ为水的重度(N/m3)，是固定常数；h为渗流层的平均厚度(m)，为了设计加工方便，故设计所有渗水管渗流层厚度均为h。

由于设计的每排渗水管的渗水覆盖土壤面积基本相同，故实际上所有渗水管间间距相同，单排渗水管内水压处于同一高程上，则单根管内压力Pi分布基本处处相同，而根据公式（1），第排渗水管的渗透系数与该排渗水管内压力Pi之间存在下述关系：

边坡设计灌溉覆盖面积总高程H，高位储水池中自由水表面到主输水管路之间高程差为H0；第i排渗水管的高程为Hi，为了使施工方便，设计所有渗水管间距均匀分布，所以高程则以最下排渗水管为基准，第i排渗水管的高程可表达为第i排渗水管内压力Pi与输水系统的分输水管路上对应位置压力等同，故输水管路应满足伯努利方程：

滴灌系统属于一种节水装置，系统内水流流动比较缓慢，管道内水的流动基本上处于层流状态，输水系统和渗流系统内各点水流速度基本相同。为了保证各排渗水管在不同高程下的渗水能力相同，储水池表面压力P0和第i排渗水管的管内压力Pi应满足下列伯努利方程：

第i排渗水管的渗透系数可表述为：

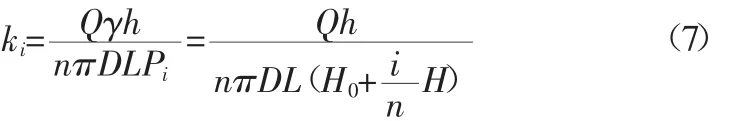
由于边坡设计灌溉覆盖面积总高程H和高位储水池中自由水表面到主输水管路之间高程差H0是已知，因此根据公式（7）得到第1排渗水管的渗透系数：

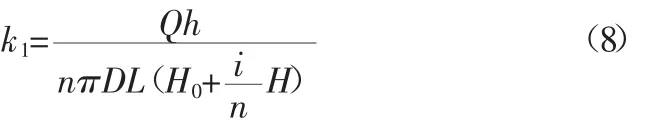
若H0较小或供水主输水管路有漏口，则H0≈0，第1排渗水管的渗透系数k1可化简为：

则第i排渗水管的渗透系数ki为：

即每排渗水管与其高程之间存在反比例关系。

3 边坡地形及滴灌系统尺寸对灌溉的影响

本章根据具体实例分析边坡地形需求与本灌溉系统的设计尺寸之间的关系。边坡地形可大可小，本章中设计一个最高位置H=10 m、斜坡角度45°的人造边坡模型，该模型横向长度L=30 m，该边坡灌溉需水量为每平方米0.001 m3/s，则该边坡实际需求量Q=0.3 m3/s。灌溉用渗水管直径D=0.014 m，包裹渗透层厚度h=3 mm，而高位蓄水池与主输水管路之间高程差为H0=0.05 m。一般渗水管排布间距越小，其灌溉覆盖均匀性越好，但这样会导致施工难度加大，故每排渗水管之间至少间隔0.5 m，故按照0.5 m设计该算例中渗水管间距，则该边坡地形中可以安装的渗水管数量：

按照上述参数求得，第1排渗水管k1=8.53 m/h。然后对比忽略H0对各排渗水管渗透系数的影响。图3为忽略储水池高程与不忽略储水池自由面高程两种计算结果的对比图。

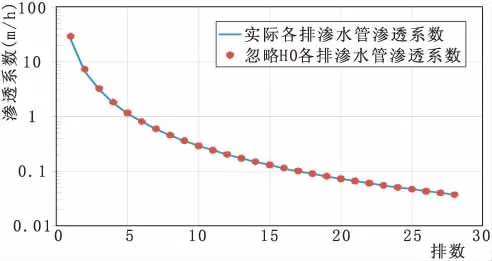
图3 忽略储水池高程对计算结果影响

从图3中可以看出，除了第一排渗水管渗透系数结果差距较大，后面的计算结果差距十分小，几乎完全可以忽略掉。

该灌溉系统设计参数主要和边坡地形有关，在保证底边一定的情况下，边坡角度的改变也会使渗透系数的参数发生变化，图4为不同边坡角度下渗透系数变化。

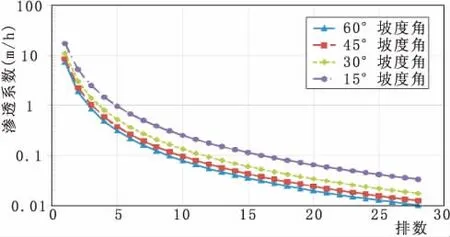
图4 坡度角对系统渗透系数设计影响

从图4可以看出，随着边坡角度减小，边坡趋于平稳，则每排管使用渗透层的渗透系数逐渐增大。这是由于高程减小，导致灌溉重力势能减小，需要提高渗透系数才能保证灌溉需水量。

如果对灌溉渗水管直径进行修改，则也会直观地影响渗透系数的设定，这是由于渗水管的直径会直接影响表面渗透层的渗水接触面积。图5为不同直径渗水管对应渗透系数设计的影响。

图5 渗水管直径对渗透系数设计影响

从图5中可以看出，随着管道直径的增加，渗水管渗透系数整体趋于变小，故为了保证加工可实现，直径不宜过大，在保证不堵塞的情况下尽量缩小管道直径。渗水管包裹的渗透层是实现灌溉节水的关键所在，故包裹层厚度也直接决定整个滴灌系统的灌溉能力。图6为不同渗透层厚度设计使用情况下对渗透系数设计的影响。

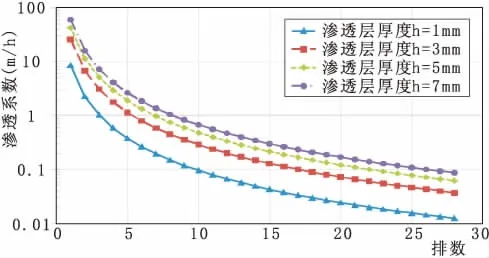
图6 渗透层厚度对渗透系数设计影响

从图6中可以看到，随着渗透层厚度增加，渗透层的渗透系数逐渐增大，故在设计时如果考虑保证等效灌溉能力的情况下，设计使用渗透系数更大的渗透层可以用更厚的渗透层来实现节水。

4 结论

本文介绍一种新型设计的灌溉系统，该系统可以应用于边坡人工再造种植植被中使用，并同时实现节水和灌溉功能的作用。本文中提及的该系统主要功能体现在渗水部分，渗水管外侧包裹可渗水的多孔材料，根据该设计建立了滴灌系统的数学模型，求解出渗透层渗透系数与滴灌系统各设计参数之间的数学关系，并根据实际设计情况假设其在边坡地形中的应用情况，对设计参数进行影响因素分析，目前得到以下结论：

（1）基于均匀滴管原则，将不同渗透系数的渗水管进行组合排列，设计了一款新型的边坡地形的灌溉系统。该系统可良好的将灌溉水资源均匀分配到整个边坡种植层中，大大提高了水资源的利用效率。

（2）基于流体力学和渗流力学原理，建立了滴灌系统灌溉水流动的数学模型，形成了一套不同高度渗水管渗透层的渗透系数的优化方法。

（3）经过算例计算，渗透层渗透系数与边坡高度成反比关系，当主输水管道压头约等于位头时，各个高度的渗水管渗透层系数近似等于其位头倒数与第一排渗水管渗透层的渗透系数的乘积。

（4）边坡地形与灌溉系统设计参数对渗透系数设计有重要影响，在保证边坡需水量的情况下，应针对系统内不同参数的相互影响关系，根据实际生产能力，近似选取合适的设计参数，更好地实现灌溉的均匀性和节水性。

依据本文设计的滴灌系统，可以实现边坡人工再造植被灌溉的均匀性和较好的节水功能，故根据该系统建立的数学模型可以正确的反映系统设计参数之间的相互影响关系。该影响关系可更好的应用于边坡地形的滴灌系统设计优化中，使矿山环境修复创面修复等人工再造植被的灌溉问题得到解决。