自由渗流面及渗流量推求的数值计算方法探讨

，，

(1.江苏省地质调查研究院，江苏 南京 210018；2.南京市测绘勘察研究院股份有限公司，江苏 南京 210005；3.河海大学水文水资源学院/河海大学水文水资源与水利工程科学国家重点实验室，江苏 南京 210098)

自由渗流面与地下水潜水水面特征相似，具有复杂的非线性，是河流等地表水入渗补给地下水、大坝渗流等定量化计算的难点，目前，尚未发现确定自由渗流面的解析法，在实际工程应用中常用数值方法求解。求解该类问题的数值方法可分为两类：变网格法和固定网格法。由于变网格法操作复杂，容易使计算网格畸变，难以处理存在水平介质分层及各种复杂夹层的情况等缺点,因而研究较少。为此，国内外学者提出了许多与固定网格法相关的处理技术，主要有剩余流量法、初流量法、节点虚流量法、单元渗透矩阵调整法、复合单元法及截止负压法等[1-6]。但这些处理技术大多方法复杂，操作困难，应用不便。

本文利用开源地下水数值模拟软件MODFLOW[7]及SUTRA[8]，提出了采用干湿单元转化、缓变渗透系数矩阵法推求自由渗流面的方法，成功推求了自由渗流面，有效地提高了目前河流与地下水交互作用计算的求解精度。

1 典型自由渗流面问题

典型自由渗流面问题可概化为图1所示。为简化求解难度，一般假设：(1)土壤均质各向同性；(2)毛管作用及蒸散发作用忽略；(3)水流服从Darcy定律；(4)稳定水流。基于以上假设可建立渗流问题的数学模型：

(1)

式中：h为水头/m；y为相对高程/m；Ks为饱和渗透系数/(m·s-1)。

为便于建立数值模型，并不失一般性，假定上、下河道水头y1=6 m，y2=1 m，渗流区距离x1=4 m。对于均质各向同性土壤介质中稳定流问题，渗透系数对自由面计算无影响，故可设定为任意值，如采用Ks=10-5m/s。

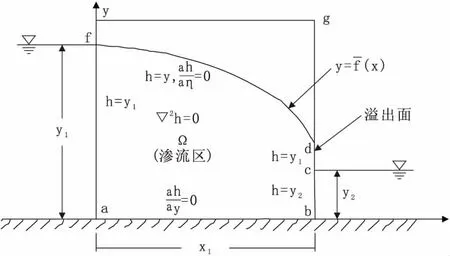
图1 渗流概化图

2 数值法求解

2.1 MODFLOW求解方法

MODFLOW是美国地质调查局开发的模拟三维地下水运动的数值计算软件。该软件采用有限单元差分法离散地下水水流方程，广泛应用于地下水数值模拟及地下水资源管理。MODFLOW将单元格分为四类：无效单元格、完全饱和单元格、部分饱和单元格、定水头单元格。前三种类型可通过输干及再湿润等处理方法相互转化。当计算单元(i,j,k-1)水头hi,j,k-1大于底板高程hb(hi,j,k-1>hb)时，无效单元格转为有效计算单元格，初始水头hi，j，k=C(hi,j,k-1-hb)+hb，其中C为水力传导系数，该过程称为浸润；当hi，j，k

自由渗流面附近的计算单元格为部分饱和单元， MODFLOW通过将这些单元的导水系数设置为T=Δh×Ks(其中Δh=hi，j，k-hb)，再利用调和平均、对数平均等处理技术计算单元格间的传导能力，很好地解决了这些单元格的水流计算问题[7]。

在MODFLOW推求自由面问题方面，可采用排水沟方法模拟稳定自由渗流面，但排水沟水位设置十分重要，如果排水沟水位设置不当，引起干湿单元转化混乱，溢出点附近水位有奇异变化，从而致使计算不稳定[9]。

本文将图1中渗流区域划分为300×200个计算单元，设定MODFLOW为稳定流计算模式，式(1)中边界条件设置如下：af、bc概化为定水头边界；ab不透水边界(无需直接设置，MODFLOW默认的边界即为不透水边界)；fd为自由渗流面，无法直接给定，可在计算迭代中求出。具体计算方法为：利用MODFLOW中计算单元格的有效、无效及定水头属性设置功能，将自由面右侧的单元格设置为无效单元格，这是因为自由渗流面为单调函数，其右侧无水流运动，通过迭代不断调整计算单元格活动、非活动属性直至收敛；cd渗流边界，将该处单元格设置为定水头，其水头设置为单元格顶板高程，由于MODFLOW采用单元格水深计算单元格导水系数，这种设置可保证溢流面排水通畅;在初始设置中可将整个bg设置为渗流边界，迭代过程中非渗流单元格会被剔除(被设置成了无效单元格)。按以上方法设置的数值模型求解得到的渗流区自由水面线及流场水头分布分别见图2和图3。

2.2 SUTRA求解方法

SUTRA是美国地质调查局研发的用于模拟变密度、变饱和度水流运动及溶质运移的数值模拟软件。该软件采用Galerkin有限元法离散非饱和水流运动方程(Richard方程)及溶质运移方程，广泛应用于海水入侵模拟研究[8][10]。

利用SUTRA构建图1中渗流区域的数值模型，网格剖分及边界条件处理与MODFLOW相近：af、bc概化为定水头边界，ab为不透水边界；fd为自由渗流面，无需直接给定。但对于渗流边界cd，由于SUTRA不能剔除非计算单元格，因此不能采用定水头模拟，而边界cg段计算节点具有如下特征：(1)溢流段cd，计算节点压强为0；(2)非溢流段dg，溢流量为0，因此可在SUTRA中将cg设置为变水头边界，依据临近计算节点判定cg段计算节点压强值：若临近节点压强大于0(饱和)，则该节点位于渗流面处，压强为0，反之，可判定该节点位于非渗流面外，压强设置为临近节点压强。

SUTRA程序未对计算节点分类，不能随意剔除非水流区计算节点。通过设置渗透系数来区分水流区及非水流区计算节点的单元渗透矩阵调整法处理技术，具有方便简洁优点。党发宁等人[11]提出了变单元渗透系数法，该方法将自由面以下的计算单元设置为饱和渗透系数，自由面以上单元近似设置为0，重新建立总体渗透矩阵，试图消除非饱和区对自由面渗流求解的影响，但是该处理方法会造成自由面附近的高斯点求解结果出现振荡、稳定性差等问题。马淑芝等[5]、付延玲等[12]提出并改进了复合单元渗透矩阵调整法，他们将罚函数引入自由面附近单元格，减少离散矩阵的奇异性。裴利华[13]研究认为单元渗透矩阵调整法求出的单元渗透系数矩阵不能真实反映渗流区透水特性，且矩阵的主系数不占优，影响计算精度和稳定性，并且对于三维问题，自由面穿越的单元形式很复杂，数学上不易处理，程序工作量很大。

本文先按传统的单元渗透矩阵调整法将计算结点分为两类：饱和节点与非饱和节点，非饱和节点渗透系数近似为0，饱和节点渗透系数为饱和渗透系数。这种设置求出的渗流区自由水面线及流场水头分布分别见图2和图3。在溢出点附近计算水头出现奇异变化，计算过程中出现不稳定，且较难收敛，这主要是由于渗透系数矩阵突变型设置导致雅克比矩阵不能满足严格对角占优，采用迭代法求解线性方程会引起数值震动。因此为提高求解结果的稳定性，需引入缓变型渗透系数矩阵。由于非饱和渗透系数函数描述从饱和到干涸过程渗透系数的缓变过程，因此，通过引入非饱和渗透系数函数可解决传统单元渗透矩阵调整法不稳定性问题。

SUTRA采用Van Genuchten-Mualem(VGM)模型描述非饱和渗透系数[14]：

(2)

式中：p为水压/pa；K为土壤非饱和渗透系数/(m·s-1)；α，n，m为VGM模型经验参数，其中m=1-1/n。

对于非饱和区渗透系数K，由式(2)可知，当α→∞时，K→0。因此，如采用α取较大值方法，进行饱和、非饱和水流计算，求解自由面问题，可避免在益处点附近计算水头奇异变化及数值解不稳定问题。当α=0.002/pa、α=0.000 05/pa、n=2时计算的渗流区自由水面线及流场水头分布分别见图2和图3。由图可以看出，当值α较大时，自由水面线推求结果虽然仍存在水头震荡变化，但计算稳定性有较大提高。

图2 三种方法求得的自由水面线(a)及其局部放大图(b)

表1 边界出入流量表 ×10-5/m2·s-1

(a)MODFLOW(b)SUTRA变渗透率法(c)SUTRA改进变渗透率法

MODFLOW、SUTRA传统单元渗透矩阵调整法和SUTRA缓变渗透系数矩阵法求得的溢出点(d点)高程分别为3.25 m、3.22 m、3.24 m，与甘油试验[15]结果(3.25 m)对比可知，MODFLOW求解精度最高。图2和图3中比较三种方法表明，缓变渗透系数矩阵法相对于传统单元渗透矩阵调整法稳定性有较大提高。三种方法求得的边界出af段入流量、bc段出流量及cd段溢流量见表1，MODFLOW和SUTRA缓变渗透系数矩阵法求得的af段入流量一致，MODFLOW、SUTRA传统单元渗透矩阵调整法和SUTRA缓变渗透系数矩阵法求得的bc段出流量无显著差异，但SUTRA模拟的cd溢出段出流量比MODFLOW模拟结果偏小。

3 结语

MODFLOW、SUTRA传统单元渗透矩阵调整法及SUTRA缓变渗透系数矩阵法求解结果表明采用MODFLOW运用干湿转化技术求解自由渗透面的方法稳定性最好、精度最高，但MODFLOW中的有限单元差分方法要求计算网格为矩形网格，矩形网格难于刻画复杂形体，致使MODFLOW应用方面存在较大局限性，而采用缓变渗透系数矩阵法的SUTRA程序，改善了传统单元渗透矩阵调整法的不稳定性，提高了数值计算精度，避免了MODFLOW必须矩形网格的局限性，是一种计算自由渗流面，估算地下水与河流水量交换量的实用方法。