一种Mecanum轮全向移动平台的设计*

章玮滨，唐 炜

(江苏科技大学 机械工程学院，江苏 镇江 212003)

0 引 言

轮式全向移动机构在平面内具有3个自由度，可做前后直线运动、横向侧移运动、斜45°直线运动、原地回转运动及任意组合运动[1]。全向移动主要依靠全方位轮组来实现，Mecanum轮因其具有结构紧凑、运动灵活稳定等优点，已发展为全方位轮组机构的主要研究热点[2-3]。Mecanum轮全向移动机构具有传统移动机构无法相比的优点，工作空间小、效率高，已在仓库储运等作业场合狭小的领域得到了应用。

建立运动学模型是分析全向运动能否实现的理论基础。目前，对全向移动平台进行运动学建模主要有矢量分析法和矩阵变换法。文献[4-6]中采用的是后者，虽然建模比较简单，但该方法使用标量分析，导致通用性较差，且在地面不平整时完全失效；文献[7]中研究了Mecanum轮的原理并做了运动仿真;文献[8]中研究了Mecanum轮采用Solidworks API的参数化实体建模的可行性。但上述研究都只做了运动分析和算法仿真，缺少样机的实验验证，且对Mecanum轮技术的工程化应用涉及甚少。

在研究平台全向移动原理的基础上，本文将采用矢量分析法建立逆运动学模型，并为其设计一套嵌入式控制系统，最后借助测距传感器对其进行运动性能测试。

1 Mecanum轮全向移动平台机构的设计

1.1 机械本体的设计

Mecanum轮主要由轮毂、辊子、支撑体3部分组成，其辊子与轮子之间成一个偏置角，由此来分解前进时车轮旋转的力，通过四轮的配合，即可实现全向移动。文献[9]中研究了辊子轮廓的曲线参数方程，其解析式较为复杂，为计算方便，本文采用椭圆曲线加以近似。为减少辊子的磨损和噪声，为每个辊子包上一层硬质橡胶材料作为缓冲，并降低Mecanum轮的安装要求。

本文研究的全向移动平台由4个Mecanum轮组成，采用四轮驱动，即由4个直流电机通过减速器分别独立驱动各个Mecanum轮。平台运动时，安装于其中的微控制器(microcontroller unit，MCU)协同控制各直流电机的转速和转向，使平台实现一系列全方位运动。为简化分析，将车体视为刚体，忽略因受力产生的轻微变形，并假设车轮与地面无相对滑动，仅存在纯滚动。其装配模型如图1所示。

图1 全向移动平台三维模型

传动装置安装于Mecanum轮径向侧边。对于行星轮减速器，通常将动力输出轴和电机轴采用平行安装的方式，多数需要使用联轴器使动力传递到车轮。本设计需要实现Mecanum轮的单独控制，因此，在结构上需要较大的轴向空间。该设计采用涡轮蜗杆减速器，其输入轴和输出轴呈直角，能大大提升机械结构的紧凑性。

笔者设计的减震机构类似于车辆的纵臂式悬架结构，Mecanum轮用带座轴承和摆臂与车体连接，在摆臂上方安装弹簧减震器与车架连接。该减震机构可使Mecanum轮在垂直平面内摆动，减小车身物理参数的变化，从而提高控制精度。

1.2 全向移动原理

全向移动平台运动时车轮的受力分析如图2所示。

图2 全向移动平台受力分析

由图2可知：4个车轮的角速度大小相等，方向可由右手定则解出。平台移动时，辊子和地面之间的接触摩擦力与车轮运动方向相反，由该摩擦力分解而来的沿辊子轴线的摩擦力Fa是平台驱动力的主要来源，另一支分解力为垂直于辊子轴线的法向力Fr，由于该滚动摩擦力相对要小很多，通常可忽略。在图2(a)中，将4个Mecanum轮着地辊子所受的轴向力Fa均分解为横向和纵向的两个分力，则四轮的纵向合力为零，横向合力方向向右，使平台向右横移；图2(b)中四轮的受力合成后将使平台实现原地旋转。

2 Mecanum轮全向移动平台控制系统设计

2.1 运动学分析

本研究采用矢量分析法对平台进行逆运动学建模，先讨论单轮的辊子中心到轮子中心的速度关系，以等式列出，再以平台为整体，分析其质心O到车轮中心的速度关系式;联立两式，经过化简可解出4个Mecanum轮与质心O之间的映射关系，即建成平台的运动学模型。

第i个Mecanum轮的结构如图3所示。

图3 第i个Mecanum轮结构原理图r，r1—轮子和辊子的半径;ei,gi—两个单位向量，方向分别为轮毂与辊子的轴线方向;P4—辊子与地面的接触点，过P4做一条直线分别与辊子和轮毂的轴线相交于R4和即为辊子和轮毂的中心;f1,h4,j—垂直于方向和沿方向的单位向量;轮毂与辊子的转速。

(1)

(2)

(3)

将式(1～3)联立，可得:

(4)

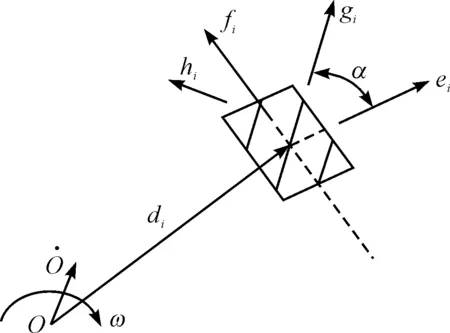
图4 第i个Mecanum轮与中心点O的关系

由图4可得：

(5)

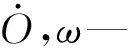
(7)

式中:α—辊子轴线与轮毂轴线的偏置角。

将4个车轮的关系式结合起来，建立起平台逆运动学模型的一般形式，即：

(7)

不难看出，全向平台若能按照不同路径运动，其中心广义速度(即线速度和旋转角速度)会随时产生变化。当轮组布局和辊子偏置角确定下来后，通过式(7)即可求出四轮的实时转速，MCU即可对4个直流电机进行协同控制，使平台实现预期的全方位运动。

2.2 系统硬件结构设计

全向移动平台控制系统的总体结构如图5所示。

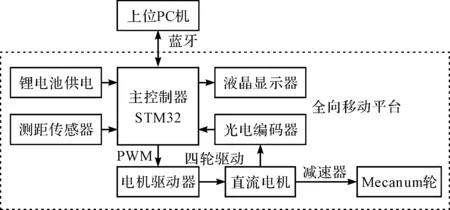
图5 控制系统基本组成

由于地面并不是完全平坦的，所以在系统实际运行时，辊子与地面的接触情况会受其影响，而降低平台的控制精度。常规PID算法的Kp、Ki和Kd这3个参数都是确定不变的，对于非线性系统往往其鲁棒性和自适应性达不到较高的要求[10]。本文采用模糊PID自整定控制算法，可在线实时对上述3个参数进行自适应调整，增强抗干扰性，提升系统的控制精度和鲁棒性。实现模糊控制有3个重要步骤：参数模糊化、模糊推理、清晰化计算[11-12]。

2.2.1 模糊化

参数模糊化即根据对应的论域范围，将输入的确定量转化为模糊量。本文控制器的输入量是误差e=r-y及误差变化率ec=de/dt.其论域为{-3，2，-1，0，1，2，3}，所对应的模糊域为{NB，NM，NS，ZO，PS，PM，PB}，分别代表负大、负中、负小、零、正小、正中、正大。在此选用三角形隶属度函数以简化算法、提高控制的实时性。在论域范围内，不论自变量取何值，其隶属度均非负。

2.2.2 模糊推理

在进行这一步前，首先分别定义ΔKp、ΔKi和ΔKd的模糊论域以及Kp、Ki和Kd各自的模糊推理规则。根据专家经验，在输入不同的e和ec的情况下，要求3个参数须对应各自模糊规则表。

2.2.3 清晰化

为了将所得的模糊量清晰化，本文采用重心法[13]，引入一个模糊变量μc(zi)对模糊值Zi进行加权计算得出清晰值:

(8)

式中:Z0—清晰值。

再通过线性变换，由Z0得到实际的PID控制量，则ΔKp的实际调整值应为:

(9)

式中:k—比例系数。

2.3 软件控制设计

上位PC机控制程序由VB.NET编写而成，主要功能是将需要设定的全向移动平台的一系列运动参数通过蓝牙发送到样机的MCU里，并在上位机上实时显示样机的运动轨迹和状态。该程序界面如图6所示。

图6 上位机控制界面

在主控制器的编程方面，使用Keil u Vision5的开发环境，采用了模块化的思想，在main.c文件中调用各个功能函数是通过含有各个功能模块的.h头文件来实现的。该编程方法可有效降低程序的复杂度，也便于后期调试和维护。其主程序流程如图7所示。

图7 主程序流程图

主程序初始化一些功能模块后，通过串口状态判断是否成功接收到指令。若成功，则根据通信协议从指令中读取到平台的一系列控制参数，并自动计算出四轮的设定转速。平台运动过程中，控制器根据定时器中断所实现的采样时间T和四轮的实际转速，更新输入参数e和ec，通过模糊PID自整定控制算法完成对小车的反馈控制。

3 实验分析

为验证本文所设计的嵌入式控制系统的实用性，以及模糊PID自整定算法的实际控制效果，笔者通过实验对平台样机运行的稳定性和重复性等方面进行综合评价。

3.1 实验方法

在划定的矩形范围内，本研究借助平台四边上安装的超声波传感器来实时获取其横向和纵向的运动距离，并通过STM32片内的数模转换器将电机转速转换为电压的变化，然后在示波器上得到系统的响应曲线，对比两种算法下的曲线即可直观地判断模糊PID自整定控制算法和常规PID控制算法的性能优劣。

3.2 控制算法比较

动态响应曲线如图8所示。

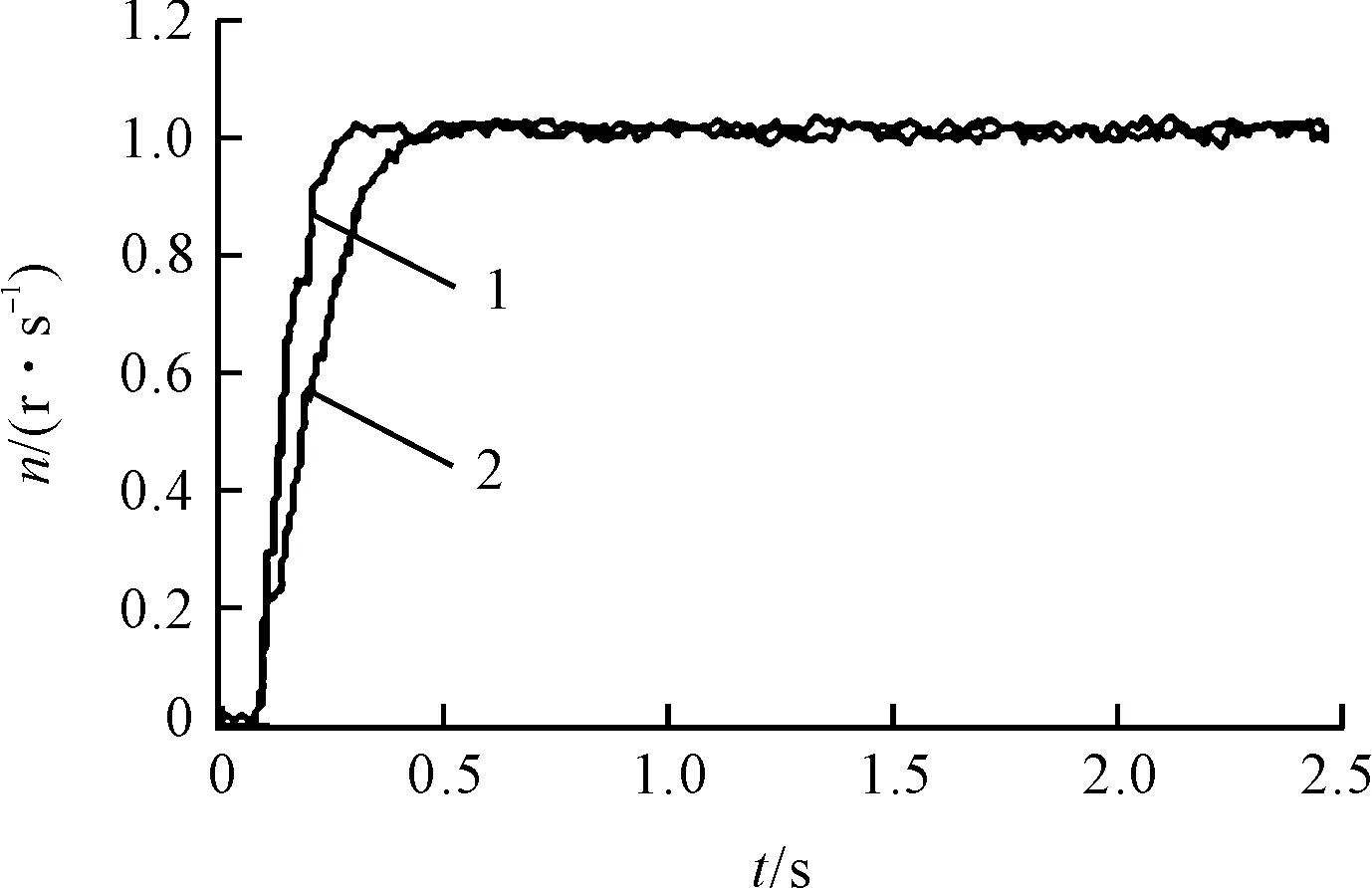
图8 动态响应曲线

两种算法的超调量最后都能稳定在零左右，而曲线1上升所用的时间t相比于曲线2有明显的缩短，分别为0.21 s和0.35 s，说明模糊PID自整定控制算法可明显改善系统的动态响应特性。当平台行驶在凹凸地面时，借助模糊PID自整定控制算法可使实际运动轨迹与理论轨迹更吻合。

3.3 平台运动实验

为评估平台的运动性能，笔者在实验室条件下对其进行了直线运动等4项实验：

(1)直线运动实验。本研究分别给平台设定20 cm/s和10 cm/s的运行速度，并通过超声波测距传感器探究实测前向距离与时间的关系。

不同速度时的直线运动图如图9所示。

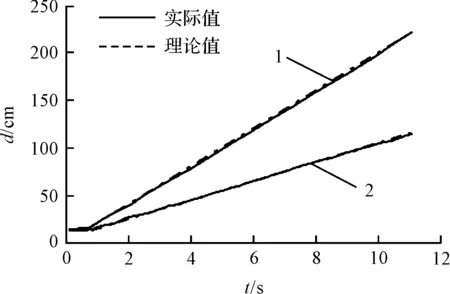
图9 不同速度时的直线运动图

(2)横向侧移实验。平台的前向距离d与时间t的关系曲线如图10所示。

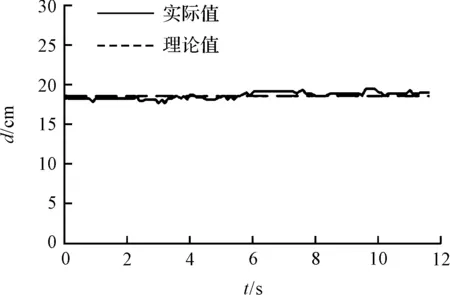
图10 横向运动图

图10中虚线表明：理论上平台应不存在前向位移。因地面存在局部不平的现象，故而车轮会发生轻微“敲地”的实际情况，造成前向距离偏移1 cm以内。

(3)斜45°直线运动实验。平台的实际轨迹与理论轨迹如图11所示。

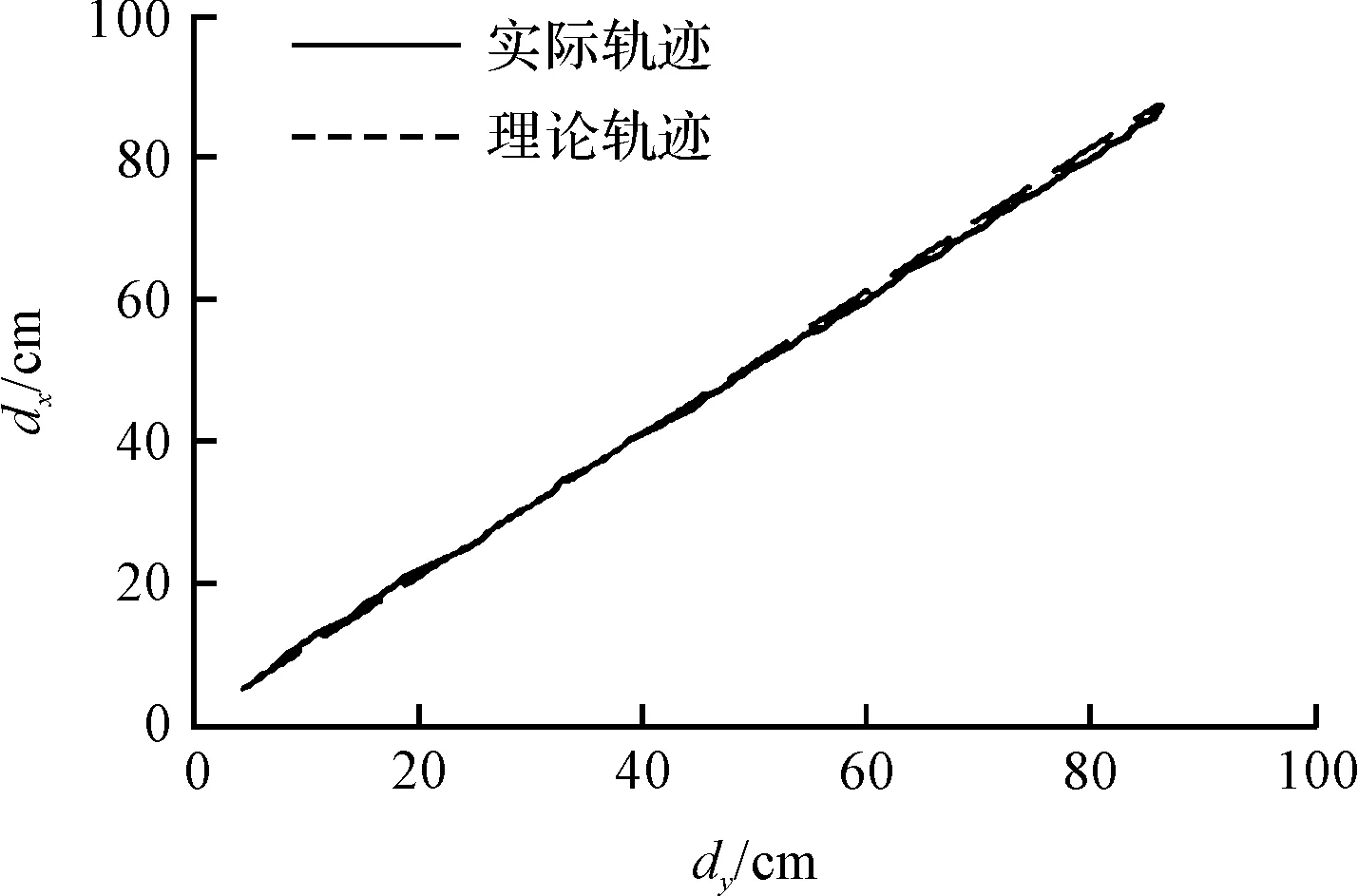
图11 斜向运动图

由图11可见：两条曲线基本吻合，平台运行平稳。

(4)3次连续矩形运动的实验测试。通过该实验测得了多次行驶轨迹的重复性误差。由于平台的惯性，在转向时会产生些许横向与纵向上的偏移量，并伴有少量旋转。在第一次直角转弯后，由于平台在换向瞬间存在少许漂移现象而造成轨迹存在些许差异；在第三次直角转弯前，由于平台在做横向侧移运动时产生了细微偏差，也造成了轨迹有些许差异。

3.4 结果分析

经过以上4项实验，表明本文对全向移动平台的运动原理分析到位，运动学模型建模准确，验证了其全方位移动性能；所设计的控制系统稳定实用，所采用的模糊PID自整定控制算法效果良好。

需要指出：由于轮组加工、平台安装及传感器本身等方面存在的误差，加之地面不是完全平整等条件限制，导致前文所假设的条件无法完全实现，且平台的重心也并不位于几何中心，上述影响因素也是实验产生偏差的主要原因。

4 结束语

在为全向移动平台建立运动学模型的基础上，本研究设计了一套嵌入式控制系统；辅以模糊PID自整定控制算法，兼顾了运算量和MCU的工作性能，能够保证控制的实时性；采用蓝牙通信和液晶屏显示等措施便利了观察和调试，同时也提升了人机交互性；最后结合测距传感器，自主设计了一系列针对全向移动平台运动性能的测试。

实验结果表明：该平台运行效果良好；该全向移动平台结构紧凑、运动灵活稳定，具有原地旋转、横向侧移等特点。