利用Mathematica软件研究声波在介质传播中量的变化①

， ， ，

(1.佳木斯大学理学院，黑龙江 佳木斯 154007；2.大庆中学，黑龙江 大庆 163000;3.佳木斯大学材料科学与工程学院，黑龙江 佳木斯 154007)

0 引 言

Mathematica软件是美国Wolfram Research公司开发的数学软件，具有数值计算、符号计算和图像处理的强大功能，使用非常方便。它具有丰富的内部函数，仅需输入简单的命令就可以快速地进行解方程、微分、积分和解微分方程等计算。Mathematica软件是目前世界上使用最广泛的数学软件之一，Mathematica软件的基本概念是用一个连贯的和统一的方法创造一个能适用于科技计算各个方面的软件系统。利用Mathematica软件可以进行一些复杂实验数据的处理，也可以将一些抽象的物理规律进行一种可视化的呈现。利用Mathematica软件展现声波在不同介质中传播频率与波矢之间的关系，以及本征振动各量之间的关系，利于探究其物理规律。

1 声波在介质中的传播

考虑速度为v的均匀流，称静止坐标系x,y,z为参考系K，引入相对于参考系K以速度v运动的参考系K'，其坐标为x',y',z'。在参考系K'中，流体是静止的，其中的单色波具有通常的形式：

φ=const·ei(k·r'-kct)

(1)

参考系K'中径矢r'与参考系K中的径矢r之间的关系为r'=r-vt。所以，在静止的坐标系中，波的形式为：

φ=const·ei[k·r-(kc+k·v)t]

(2)

在指数中，t的系数是波的频率ω。因此，运动介质中频率与波矢k的关系为：

ω=ck+v·k

(3)

根据上述公式的推理得出化简最终的结果，分别对气体、液体这两种状态的物质进行研究，画出运动介质中频率与波矢k之间的关系图，设运动介质的速度均为10m/s，以标准大气压下的空气、蒸馏水为例，已知15℃下空气中的声速340m/s，25℃下空气中的声速为346m/s，25℃下蒸馏水中的声速为1497m/s。进入Mathematica软件进行程序编写，打开Mathematica程序，进入程序主窗口。

输入编程程序进行编程：

u = 10;

c = 340;

k =5;

f[x_] = c*k + u*x

Plot[f[t], {t, 0, 100}, AxesLabel -> {"rad/m", "Hz"}]

最终得结果如图1：

再输入25℃下空气中的声速，进行编程，结果如图2：

最后输入25℃下蒸馏水中的声速，进行编程，结果如图3：

2 本征振动

研究一种平面驻声波，其中所有的量都仅仅是一个坐标(例如x)以及时间的函数，若把方程(4)

(4)

图1 15℃下空气中声波频率与波矢关系图

图2 25℃下空气中声波频率与波矢关系图

图3 25℃下蒸馏水中声波频率与波矢关系图

的通解写为(5)

(5)

的形式，则有(6)

(6)

适当选择坐标原点和计时起点，就可以使α和β为零，于是就有(7)

(7)

对于波中速度和压强，我们就可以得出(8)

(8)

以空气、蒸馏水、玻璃中的声波为例，探究波速和位置之间的关系，规定声源的振幅为1，频率为50Hz。

首先是在空气中，已知在室温293K、压强1atm情况下，空气中声速为346m/s，输入主要编程程序：

c = 346;

w = 50;

a = 1;

f[x_, t_] = -a*w/c*cos[w*t]*sin[w/c*x]

-(25/173) cos[50 t] sin[(25 x)/173]

Plot3D[-(25/173) cos[50 y] sin[(25 x)/173], {x, 0, 100 [Pi]}, {y, 0, 100}, AxesLabel -> {"位置", "时间", "速度"}]

输入Show[%32, ViewPoint -> Left]，得到图4：

图4 空气中波速与位置关系侧视图

然后是在蒸馏水中，已知在室温293K、压强1atm情况下，蒸馏水中声速为1497m/s，输入主要编程程序：

c = 1497;

w = 50;

a = 1;

f[x_, t_] = -a*w/c*cos[w*t]*Sin[w/c*x]

-((50 cos[50 t] sin[(50 x)/1497])/1497)

Plot3D[-((50 cos[50 y] sin[(50 x)/1497])/1497), {x, 0, 100 [Pi]}, {y，0, 100}, AxesLabel -> {"位置", "时间", "速度"}]

输入Show[%42, ViewPoint -> Front]，得到图5：

最后是在玻璃中，已知在室温293K、压强1atm情况下，玻璃中声速为2730m/s，输入主要编程程序：

c = 2730;

w = 50;

a = 1;

f[x_, t_] = -a*w/c*cos[w*t]*Sin[w/c*x]

-(5/273) cos[50 t] sin[(5 x)/273]

Plot3D[-(5/273) Cos[50 y] Sin[(5 x)/273], {x, 0, 100 [Pi]}, {y, 0, 100}, AxesLabel -> {"位置", "时间", "速度"}]

输入Show[%42, ViewPoint -> Front]，得到图6：

图5 蒸馏水中波速与位置关系正视图

图6 玻璃中波速与位置关系正视图

而对于波中的压强，就可以得出(9)

(9)

先是在空气中，已知在室温293K、压强1atm情况下，空气中声速为346m/s，密度为0.01205g/cm3,输入主要编程程序：

w = 50;

p = 0.01205;

a = 1;

c = 346;

f[x_, t_] = p*a*w*sin[w*t]*Cos[w/(c*x)]

0.6025 cos[25/(173 x)] sin[50 t]

Plot3D[0.6025 cos[25/(173 x)] sin[50 y], {x, 0, 100 [Pi]}, {y, 0, 100}, AxesLabel -> {"位置", "时间", "压强"}]

输入Show[%15, ViewPoint -> Left，得到图7：

然后是在蒸馏水中，已知在室温293K、压强1atm情况下，蒸馏水中声速为1497m/s，密度为1g/cm3,输入主要编程程序：

w = 50;

p = 1;

a = 1;

c = 1497;

f[x_, t_] = p*a*w*sin[w*t]*cos[w/(c*x)]

50 cos[50/(1497 x)] sin[50 t]

Plot3D[50 cos[50/(1497 x)] Sin[50 y], {x, 0, 100 [Pi]}, {y, 0, 100}, AxesLabel -> {"位置", "时间", "压强"}]

输入Show[%15, ViewPoint -> Left]，得到图8：

图7 空气中压强与位置关系侧视图

图8 蒸馏水中压强与位置关系侧视图

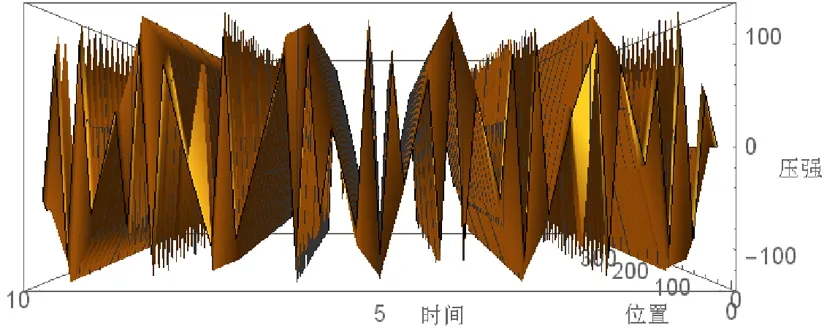
图9 玻璃中压强与位置关系侧视图

最后是在玻璃中，已知在室温293K、压强1atm情况下，玻璃中声速为2730m/s，密度为2.7g/cm3,输入主要编程程序：

w = 50;

p = 2.7;

a = 1;

c = 2730;

f[x_, t_] = p*a*w*sin[w*t]*cos[w/(c*x)]

135.cos[5/(273 x)] Sin[50 t]

Plot3D[135.` cos[5/(273 x)] Sin[50 y], {x, 0, 100 [Pi]}, {y, 0, 10}, AxesLabel -> {"位置", "时间", "压强"}]

输入Show[%15, ViewPoint ->Left]，得到图9:

3结 论

(1)相同波矢下，同种物质温度高的比温度低的声波频率大；相同波矢下,温度相同，蒸馏水的声波频率比空气的声波频率大。