基于大数据分析的复值BP神经网络方法①

,

(亳州职业技术学院信息工程系,安徽 亳州 236800)

0 引 言

目前万维网具有超过万亿的统一资源定位符(URL)，cebook 有 10 亿节点和千亿连边，大脑神经元网络有数百亿节点，中国三大运营商的手机通讯网络无一不拥有数亿用户。如何处理超大规模的网络数据，已经成为学术界急需解决的关键科学问题。

传统的数据分析方法，主要是根据以前的经验，先设计出人工模型，然后根据设计出的模型对数据进行分析，这种方式在以前是还是有效的，处理一些结构性强、数据量小的信息，但是在大数据的时代下，在使用这种方式，就会出现很多弊端，已经不能适应现代大数据的发展了[1]。另外，现在占据大数据时代的主要是一些非结构性数据，出现的模式也是不一样的，无法再根据之前的经验进行分析，再想要建立人工模型，是十分困难的，这就需要再研究相关数据挖掘技术，所以，神经网络分析方法就应运而生了，它能够从复杂、深量的数据中提取有用的信息，这就是现代的大数据分析方法。

神经网络方法主要是以深度学习为主要特点，以数据驱动、数据自动检索来提取其中的数据信息，尤其是在非结构化、模型不明且多变、跨领域的大数据上更具有显著优势，复值BP神经网络方法主要是通过在内部构建许多隐形的机器模型和大量的数据分析训练，从而得出准确的数据信息，随着大数据时代的不断深入，大数据所含有的信息量也十分丰富，只有想神经网络这种更加复杂、更有表达能力的模型，才能够挖掘出其中的内在信息。

1 大数据分析

在数据系统中，大数据主要是经过了五个重要环节，数据准备、数据存储和管理、计算机管理、数据分析和知识再现五个重要环节，数据分析阶段占据核心地位，主要是体系在3V方面，从体量巨大、增长迅速和类型多样三个方面来进行分析，得出规律和结论，只有通过进行数据分析才能够挖掘大数据中更有深度、更有价值的信息，得到大数据的第四个特性—价值，所以说数据分析在大数据时代显得尤为重要，是从数据转化为信息的重要一环[2]。

大数据的4V特性对于大数据分析也是一个重大挑战，现在全球每年的数据增长速度基本上都是去年的两倍左右，相当于美国国会图书馆大约2500万个，对这样庞大的数据分析是十分苦难的，从每个人手中的智能手机到显示器上的传感设备等，都无时无刻不再发生着复杂的结构性或者非结构性的数据变化，结构性的数据变化相对来说比较容易分析，但是往往数据的出现是以非结构性出现的，这就给大数据分析更增添了一些难度，有相关的研究调查指出，在以后大约10年的时间内，非结构性的数据将会占据到90%左右，数值型的结构性数据将会得到更加深入的分析和研究，这就相当于传统的数据研究领域，包括网页索引、社交数据等，都在一些大型互联网公司中得到很浅的分析，但是对于像文本、信息、图片、视频等这些占据了总数据量约85%的非结构性信息却是很难进行有效分析。

2 神经网络

2.1神经网络的结构

神经网络是属于人工智能方面的链接主义学派，和人大脑中的神经突触一样，能够进行信息的传递和处理。第一代的神经网络感知机诞生于20世纪50年代，它主要是实现线性分类以及联想记忆，能够解决的问题比较少，而出现在20世纪80年代的反向传播算法就能够在解决现行不可分问题上广泛应用，因为它能够进行多层感知和训练算法，但是由于当时硬件的计算能力和网络训练算法还都比较落后，这就掣肘了神经计算方法的发展，直至到了2006年Hinton教授提出的深度教学方法，多层结构、逐层学习，这才真正使得神经网络方法在大数据时代发挥了强大的计算能力，并逐渐在大数据时代分析下明亮起来，它主要运用在语音识别、图像识别以及自然语音识别等方面，现在这些领域做出了很大的突破性成功，而且随着大数据时代的不断深入，神经网络方法的不断探索，已经在不少领域内取得了标志性的记录。

2.2 复值BP神经网络学习方法

大部分的神经网络方法还都是运用前馈神经网络，根据字面意思，就可以知道数据在这种网络中流向是属于单向性的，即是说从开始的输入到输出是一条线传递的，中间逐层进行映射和传递，网络的深度，也就是说在神经网络中神经元层次的数量，之间通过很多隐形的神经元数量，各个神经元之间相互链接，开始对原始数据进行特征分析，根据神经网络中的逼近原理，任何一个非线性映射，都能够找到一个浅层网络和一个深层网络，而且能够在任意精度的情况下无限逼近，出现这种情况是有条件的，要使得浅层网络的隐形神经元足够多，深度网络的做的足够深，但是浅层网络和深度网络相比较，深层网络只要能取得一定数量的参数就可以有相同的逼近效果，而不需要和浅层网络大量的参量[3]。复值BP神经网络是在神经网络的基础上延伸的，构成了一个全新的网络模型，每个网络之间是互相连接，如图1所示。

图1 复值BP神经网络模型

2.3 复值BP神经网络的训练过程

复值BP神经网络学习模型相对复杂一些，一般就是由几个相对简单的模块对层次堆积起来的，这里面的每个模块都是将从输入到输出的非线性映射，而且，在映射时，每个模块都能够对输入具有选择性和不变性，一个神经网络具有多层非线性层，往往具有5到20左右的深度，就可以根据选择性，对一些很小的细节进行选择，可以非常敏感，同时，对其它细节可以不敏感，这就是神经层的选择性，例如背景，就因为敏感度不同，所以出现的图像、颜色等都不一样。

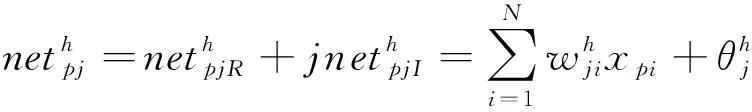
(1)

假设R和I分别代表的是实部和虚部，可以得到隐层神经元输出值为公式(2)所示

(2)

则输出神经元输出方程为公式(3)所示

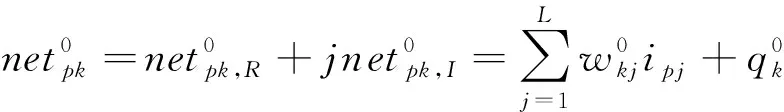
(3)

通过上式可以得到神经元的输出为公式(4)所示

(4)

复杂神经网络基于反向传播过程来计算目标函数相对于每个模块中的参数的梯度。反向传播过程的数学原理即为链式法则。目标函数相对于每个模块的梯度具有一定的独立性，这是链式法则的关键，目标函数相对于一个模块的输入的梯度可以在计算出目标函数相对于这个模块输出的梯度之后被计算，反向传播规则可以反复施加通过所有模块传播梯度，从而实现梯度(亦即误差)的不断反向传播，从最后一层一直传播到原始的输入。BP复值神经网络的反向传播定义一个输出神经元的误差为δpk=(Dpk-Opk)，其中p代表的是第p个训练向量，k代表第k个输出神经元，最小误差所有输出神经元的平方和如公式(5)所示。

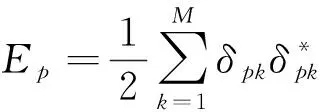
(5)

根据系数的实部和虚部进而对Ep的梯度的复值进行计算，权值的实虚部形式如公式(6)所示。

(6)

根据上式可以得到输出层权值更新的公式(7)

(7)

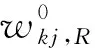
(8)

根据前面的定义表达式可以进一步得到公式(9)

(9)

通过上面公式可以得到隐层误差公式(10)所示

(10)

3 在语音识别和图像理解的应用实例

许多的经典学习算法是出现于上世纪九十年代，但是大数据时代的浪潮不断推进，各种各样更加强大的计算机设备也就随之不断更新，各种训练深层的网络新思路也踊跃的提出，这些新的思想、新的科技都在现实中得到了充分的运用，这些深度的学习都在实际运用中得到替身，无限深度学习可以利用各种海量数据，而且能够从这些数据中提取出所蕴含的相关信息，并通过抽象知识进行表达，这就是把原始的数据转变为某种知识，运用无限深度学习能够大大提升数据信息的运用准确性，在这几年的短时间内，就能够在语音理解、图像理解、文本理解等众多领域找算法设计思路，逐渐形成各种模型，然后输出最后的结果。虽然在优化方面还比不上深度神经网络，但是目前出现的BPTT、LST等出现为这一问题提供了解决方案。

4 结 语

尤其是随着大数据时代的不断推进，基于回复式网络结构的无限深度神经网络计算方法也在学术界和工业界得到了越来越广泛的关注，并迅速在许多大互联网公司成为研究的重点，神经网络在处理时序问题上具有很大的潜力，大数据的分析和预测功能在强大的互联网上显示出更加强大的能力，随着结合智能计算的大数据分析日益成为大数据时代的热点问题，神经网络方法也就在更多领域被提出更多新的思路和方法，它的应用也必将会刷新更过领域的奇迹，推动和大数据分析的发展和革新。