导频序列长度对多用户大规模MIMO FDD系统速率的性能影响及优化

王毅，马鹏阁，黄开枝，李春国，黄永明，杨绿溪



导频序列长度对多用户大规模MIMO FDD系统速率的性能影响及优化

王毅1,2，马鹏阁1，黄开枝2，李春国3，黄永明3，杨绿溪3

（1. 郑州航空工业管理学院电子通信工程学院，河南 郑州 450046；2. 国家数字交换系统工程技术研究中心，河南 郑州 450002； 3. 东南大学信息科学与工程学院，江苏 南京 210096）

针对多用户大规模MIMO FDD下行链路系统，分析了导频序列长度随基站天线数变化时对系统下行遍历速率的渐进性能影响。利用确定性等价原理，推导出遍历速率的解析表达式，基于此分析得出：归一化导频开销（导频序列长度与天线数之比）趋近于0时，仍可满足传输速率随基站天线数增加而无限增加；固定导频序列长度而只增加基站天线数，系统传输速率将出现饱和效应。进一步地，在有限的信道相干时间内，以系统和速率最大化为目标来优化导频序列长度，并在特殊相关信道模型下，借助于Lambert W函数，推导最优导频序列长度的闭式解。仿真结果验证了理论分析的正确性和最优导频序列闭合解的有效性。

大规模多输入多输出；频分双工；导频序列长度；下行速率；渐进性能

1 引言

无线数据业务量的迅猛增加以及无线传输场景的多样化应用需求对5G系统提出了千倍容量提升、极低端到端时延、高速移动应用、海量设备接入以及高能效等多方面的指标要求[1-2]。为了实现5G系统的这些核心技术指标，产业界与学术界也提出了众多备选技术[3-5]，其中，大规模多输入多输出（massive MIMO, massive multiple-input multiple-output）技术深入挖掘潜在的空间维度资源，通过在基站配备比现有多天线系统（如4G LTE-A）高若干数量级的天线阵列（几十到几百甚至上千根天线）来同时服务多个用户，在不需要增加额外的时间、频率和功率资源条件下，便可在频谱效率、能效、多用户干扰消除、空间分辨率以及上层调度等方面获得巨大的性能优势[6-9]。也正因为如此，大规模MIMO技术一经提出便吸引了无线通信产业界和研究机构的众多目光，并被普遍认为是5G系统的物理层关键技术之一[7]。

值得注意的是，大规模MIMO技术所带来的这些性能提升是以基站获得良好的信道状态信息（CSI, channel state information）为前提的[6-9]，而信道估计作为获取CSI的重要环节，将影响着整个系统的性能。针对通信系统的2种传统双工制式，即时分双工（TDD, time division duplexing）和频分双工（FDD, frequency division duplexing），大规模MIMO在获取CSI时所采用的信道估计方案以及所产生的导频开销也是截然不同的[6]。在TDD制式下，由于上下行信道满足互易性条件，可通过用户发送上行导频信号，基站端接收后再进行信道估计，由此获得下行信道CSI。因此，正交导频序列的长度将与用户数成正比，而与天线数无关，其导频开销较小[8]。而对于FDD制式，由于上下行信道不再满足互易性，只能通过基站发送导频序列，用户进行信道估计，随后用户再将CSI反馈至基站。由此，正交导频序列长度将与基站天线数成正比，从而产生巨大的系统开销，这将对系统的有效信息传输造成巨大的浪费[8]。这也是大规模MIMO技术在提出之初，众多研究人员将主要研究放在TDD制式的一个重要原因[9-12]。然而，在TDD制式下，大规模MIMO系统所受到的导频污染、上下行信道校准误差以及硬件损伤等都严重影响其性能。而FDD制式下，系统可提供较TDD系统中所没有的特殊优势，如低时延、对称业务等[13]。与此同时，在现行的蜂窝通信体制中，主要采用的双工制式仍是FDD。从全球范围内各国颁发的4G 牌照来看，针对FDD制式的牌照超过300多张，而TDD制式的牌照仅有50余张[14-15]。因此，考虑到4G到5G系统的平滑演进和过渡，解决FDD制式下大规模MIMO技术中存在的导频开销问题将具有十分重要的理论价值和工程意义。因此，国内外研究机构也逐渐将目光聚焦于大规模MIMO FDD系统的研究中来。

虽然大规模MIMO FDD系统中的CSI获取面临着较大的困难，但是国内外学者已经从信道估计方案、导频信号、量化反馈以及预编码设计等不同方面进行了研究，并取得了一些初步成果。文献[16]在密集用户场景下，提出了基于信道统计信息的降维信道双层预编码方案。该方案利用密集用户中存在相同或相近信道协方差阵这一特性，将不同用户进行分组，利用组间信道协方差阵的正交性消除组间干扰，从而降低了组内用户的信道估计导频开销。Dai等[17]通过挖掘无线信道的时间—空间二维稀疏性，研究了基于压缩感知低开销信道估计和反馈方案。文献[18-19]针对单用户大规模MIMO FDD系统分别研究了基于均方误差最小化和接收信噪比最大化的导频信号优化方案。文献[20]则从无线信道的角度域出发，研究设计了低开销的导频信号和信道估计方案。然而，现有针对大规模MIMO FDD系统的研究，大多是在给定导频序列长度的条件下来优化设计导频信号或预编码方案，而针对导频序列长度在系统性能中的影响所进行的分析尚未见到，且导频序列长度是大规模MIMO FDD系统中的一个重要开销指标。

基于上述分析，本文将针对多用户大规模MIMO FDD系统，研究导频序列长度对下行传输速率的极限性能影响，并在考虑导频序列开销与有效数据发送时长折中的情况下，对导频序列长度进行优化。首先，建立导频序列长度与基站天线数的不同增长速率变化关系，在基站采用最大比发送（MRT, maximum ratio transmission）预编码时，分析得出系统传输速率的渐进极限性能，并给出满足系统速率持续增长要求的导频序列长度与天线数定量关系式。进一步地，利用随机矩阵理论中的确定性等价原理，推导得出包含导频序列长度的下行传输速率解析表达式。基于此，考虑到实际系统中有限的信道相干时间，以最大化系统和速率为目标，优化导频序列长度，使信道估计和有效数据传输的时长资源得到有效分配，并在特殊信道相关阵条件下，利用Lambert W函数，推导出最优导频序列的闭合形式解。最后，利用蒙特卡洛数值仿真对本文的理论结果进行验证，并对所提出的最优导频序列长度闭式解进行验证。

2 系统模型与问题描述

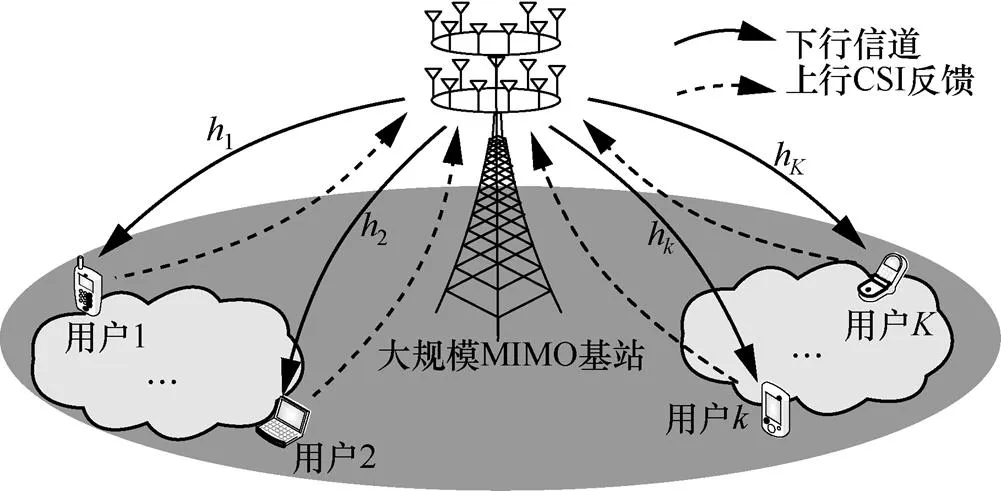
图1 多用户大规模MIMO FDD下行系统

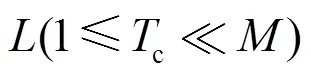
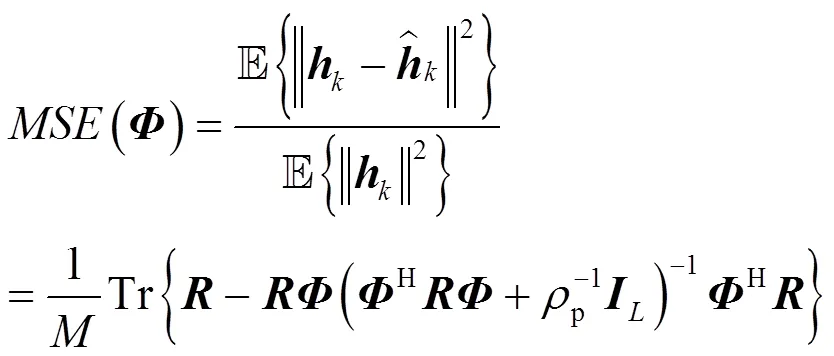
其中，有

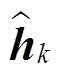
基站获取下行CSI后，假设采用大规模MIMO系统中复杂度与性能都较好的最大比发送（MRT, maximum ratio transmission）预编码方案，则基站的发射信号向量可以表示为

由于每个用户独立接收下行信号并进行检测译码，因此，第个用户的接收数据信号为

通过式(7)和式(11)可以看出，导频序列的长度将影响CSI的估计精度，进而影响预编码矩阵与实际信道的匹配程度，最终将会反映在系统的频谱效率性能。基站端天线数的大量增加，导频序列长度应该相应增长，然而有限的信道时频资源无法满足这种要求，下面将着重研究导频序列随天线数以不同的增长速率变化时对于系统频谱效率的渐进性能所带来的影响。

3 导频序列长度对传输速率的性能影响及优化

3.1 传输速率渐进性分析

由于涉及渐进性分析，此处对信道相关矩阵做如下假设[9, 22]。

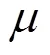
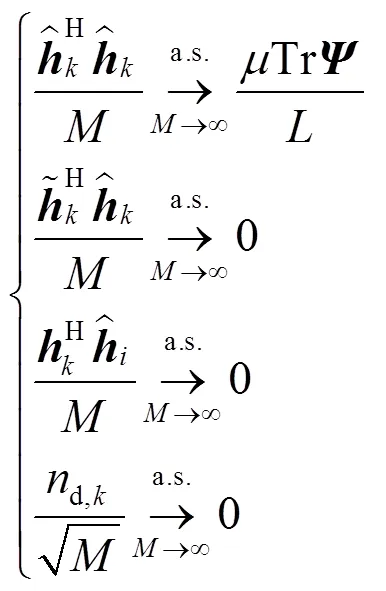
其中，式(13)的第2个和第3个计算式分别利用了信道估计向量与误差向量统计独立以及不同用户的信道向量与信道估计向量相互独立的条件，而式(13)的第4个计算式则是由于噪声变量是有限值随机变量，因而，当趋于无穷大时，其极限值为0。进一步地，利用信道相关矩阵的谱范数一致有界性条件，可以得到式(13)的第一个计算式右侧极限值为非零有界常数，即

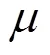
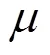
结合第1)种和第2)种导频序列长度变化条件下的传输速率渐进性性能，可以得到关于导频序列长度随天线数增长的设定准则，有如下定理。

定理1 当导频序列长度与基站天线数满足

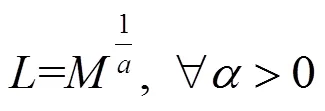
时，系统的下行遍历速率可随天线数增加而持续增长。

证明过程与式(12)和式(16)类似，此处不再赘述。

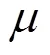
由于固定，此处不能直接采用类似第1)种和第2)种的渐进极限分析方法来获得频谱效率的极限性能，而直接通过期望运算对式(11)中的频谱效率进行分析也是十分困难的。但是，借助于大维随机矩阵理论中的确定性等价近似方法，可以得出式(11)中频谱效率的一种有效近似解析表达式，从而分析第3)种情况下的频谱效率极限性能。关于频谱效率解析表达式有如下定理。

定理2 当基站采用MRT预编码时，第个用户的遍历速率的近似解析表达式为

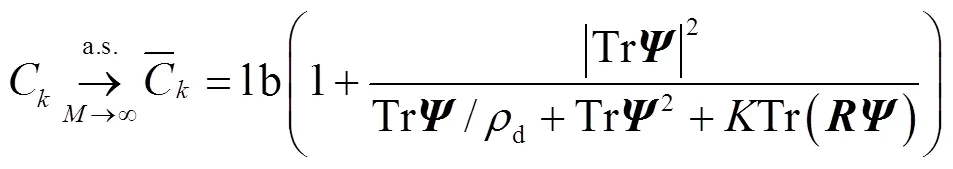
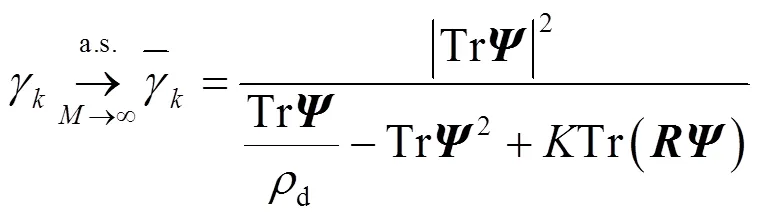
再根据主导收敛和连续映射理论[9]，可以得到传输速率C的确定性近似值为

证毕。

需要注意的是，定理2是在天线数趋于无穷大时得到的遍历速率近似表达式，且其误差也将逐渐趋于0。但是，该方法可以在给定的有限系统参数下（如天线数、用户数和导频长度等）提供遍历速率的一种精确的近似分析方法[9,16]，在后续的仿真分析中也可以看到该方法提供的解析表达式具有很好的近似效果。

将式(7)代入式(18)并化简合并，可以得到

更重要的是，定理2提供的速率闭合表达式对于第1)种和第2)种导频序列长度变化情况下的结论也是适用的。从式(22)~式(24)可以看到，当随增加时，频谱效率的上界与下界将持续增加，最终趋于无穷大，因此，在第1)种和第2)种导频序列变化情况下，系统的频谱效率将无限增大。

3.2 基于速率最大化的导频长度优化

在3.1节中分析了导频序列长度随天线数的不同变化情况对系统速率的渐进极限性能影响。在实际系统中，由于信道相干时长和相干带宽都是有限的，因此，无法持续增加导频长度来保证系统性能。同时，导频序列本身不携带任何有效信息，是一种系统开销，若在一定的信道相干时间内给导频序列分配的时长过长，则有效数据的发送时间就会相应缩短，而有效数据的发送才是通信的最终意义和目标。由此可以看出，对于一定的信道相干时间c，导频序列所占据的时长与有效数据的发送时长之间存在一个折中。

考虑信道估计导频开销情况下，系统的下行和速率为

因此，以和速率最大化为目标的导频序列长度优化问题可以建立为

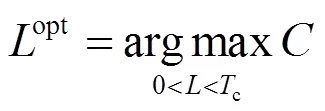
观察式(25)和式(26)可以看出，由于导频序列长度参量存在于求和号的上限，在现有的凸优化和整数优化方法都无法对其进行相应的变量松弛或放缩。同时，在一般普通的信道相关阵条件下，式(25)中的特征值也不具有任何特殊性，因此，该和速率表达式是无法再进行化简的。在此情况下，可采用遍历搜索的方法求解该优化问题。由于相干时长c是有限的，而也是整数变量，因此系统可采用离线计算。

然而，在某些特殊的信道相关矩阵和特征值条件下，通过化简并借助于Lambert W函数，本文可以进一步得到最优导频序列的闭合形式解，从而观察其解的内部结构与影响要素。下面将着重考虑如下信道相关阵[9]

证明 由于导频序列长度变量为整数变量，为了便于求解，先将其松弛为连续变量，并令式(28)中目标函数对变量求一阶导数，可以得到

从式(30)可以得到的一阶偏导数在变量边界取值具有如下极限特征

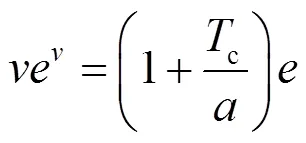
再利用Lambert W函数的定义可以直接得到

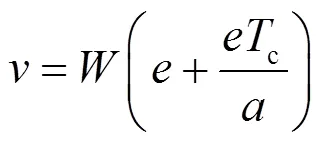
最后将和的表达式代入式(36)即可得到式(29)中的最优导频序列闭式解。证毕。

4 仿真结果与分析

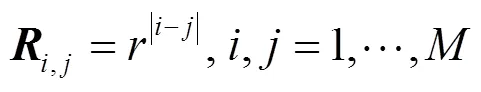
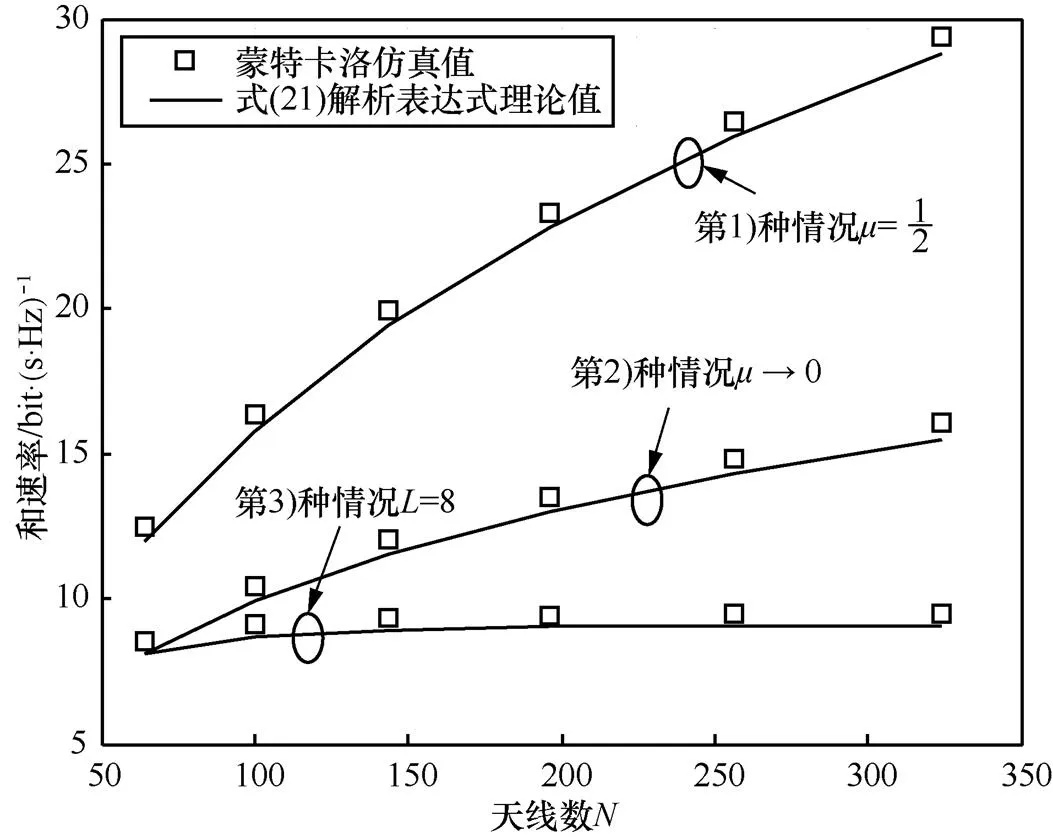
图2 指数衰减型强相关信道下，导频序列长度随天线数变化时系统的下行速率变化趋势()

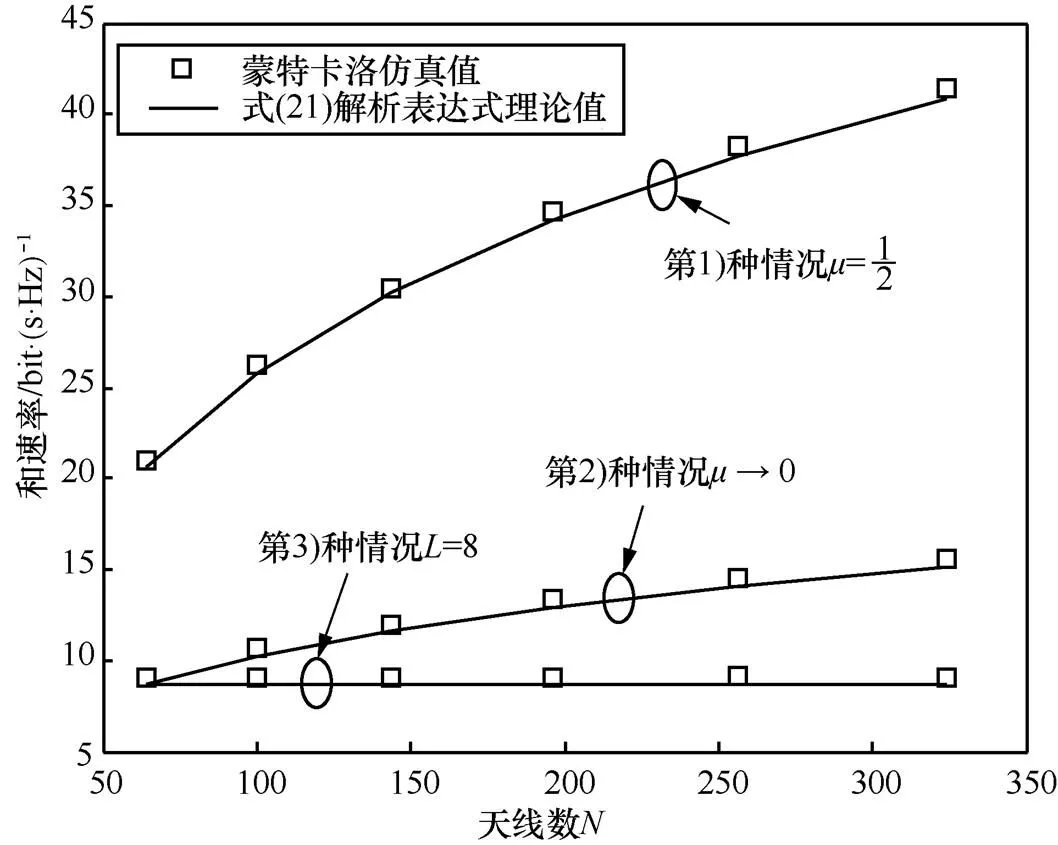
图3 指数衰减型弱相关信道下，导频序列长度随天线数变化时系统的下行速率变化趋势()

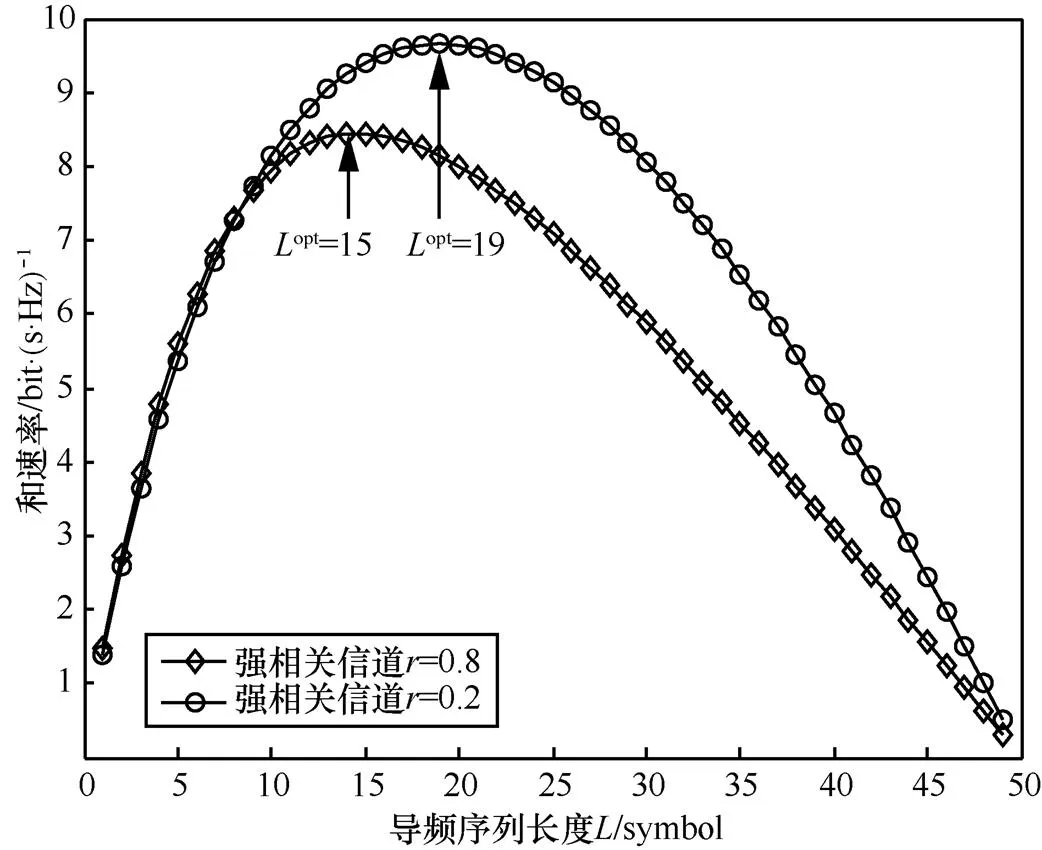
图4 考虑信道估计开销时，指数衰减型强相关和弱相关信道下，最优导频序列长度的性能对比()

图5针对特殊信道相关阵，给出了不同信道相干时长c条件下，和速率随导频序列长度的变化趋势。从图5可以看出，和速率随着导频序列长度仍然是先增后减的变化趋势，并且存在唯一的最优值，这与定理3中所给的结论完全一致。在图5中也标出了由闭合表达式(29)计算得到的最优导频序列长度理论值，具有很好的精确性。同时还可以发现，随着c的增加，系统的和速率性能呈现整体增加趋势，并且相应的最优导频序列值也呈递增趋势。这主要是因为信道相干时间的增加，使可分配给导频序列长度的时长相应增加，从而提升了信道估计的性能，进而增强了系统的和速率。

图5 考虑信道估计开销时，特殊信道相关阵下，和速率随信道相干时间的变化及对应的最优导频序列长度()

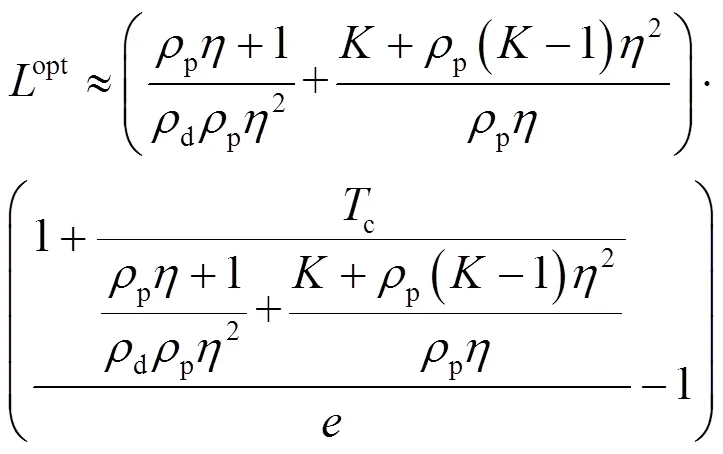
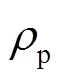
图6 考虑信道估计开销时，特殊信道相关阵下，最优导频序列长度随相干时间的变化趋势()

5 结束语

本文针对多用户大规模MIMO FDD下行系统，分析了在基站采用MRT预编码方案，导频序列长度随天线数以不同增长速率变化时，系统下行速率的渐进极限性能。通过分析发现：1)若只增加天线数而固定导频序列长度，系统速率将出现饱和效应；2)尽管归一化导频开销逐渐趋近于0，通过增加天线数，仍然可以保证系统速率持续增大。同时，给出了满足系统速率持续增长要求下的导频序列长度与天线数定量关系式。进一步地，考虑有限的信道相干时间，以最大化系统和速率为目标，对导频序列时长和有效数据时长进行了资源分配。并在特殊相关信道模型下，推导出了最优导频序列长度的解析形式解。数值仿真结果与本文所推导的结论完全一致，并且通过仿真看到最优导频序列长度的闭式解具有很好的精确性。

[1] ANDREWS J G, BUZZI S, CHOI W, et al. What will 5G be?[J]. IEEE Journal on Selected Areas in Communications, 2014, 32(6): 1065-1082.

[2] GUEY J C, LIAO P K, CHEN Y S, et al. On 5G radio access architecture and technology [J]. IEEE Wireless Communications, 2015, 22(5): 2-5.

[3] 尤肖虎, 潘志文, 高西奇, 等. 5G移动通信发展趋势与若干关键技术[J]. 中国科学: 信息科学. 2014, 5 (16): 551-563

YOU X H, PAN Z W, GAO X Q, et al. The 5G mobile communication: The development trends and its emerging key techniques[J]. Science China Information Sciences, 2014, 5 (16): 551-563.

[4] 张平, 陶运铮, 张治. 5G若干关键技术评述[J]. 通信学报, 2016, 37(7): 15-29.

ZHANG P, TAO Y Z, ZHANG Y. Survey of several key technologies for 5G[J]. Journal on Communications, 2016, 37(7): 15-29.

[5] AGIWAL M, ROY A, SAXENA N. Next generation 5G wireless networks: a comprehensive survey[J]. IEEE Communications Surveys & Tutorials, 2016, 18(3): 1617-1655.

[6] MARZETTA T L. Noncooperative cellular wireless with unlimited numbers of base station antennas [J]. IEEE Transactions on Wireless Communication, 2010, 9(11): 3590-3600.

[7] BOCCARDI F, HEATH R W, LOZANO A, et al. Five disruptive technology directions for 5G [J]. IEEE Communication Magazine, 2014, 52(2): 74-80.

[8] LARSSON E, EDFORS O, TUFVESSON F, et al. Massive MIMO for next generation wireless systems [J]. IEEE Communication Magazine, 2014, 52(2): 186-195.

[9] HOYDIS J, BRINK S T, DEBBAH M. Massive MIMO in the UL/DL on cellular networks: how many antennas do we need? [J]. IEEE Journal on Selected Areas in Communications, 2013, 31(2): 160-171.

[10] NGO H Q, LARSSON E G, MARZETTA T L. Energy and spectral efficiency of very large multiuser MIMO systems [J]. IEEE Transactions on Communications, 2013, 61(4): 1436-1449.

[11] 李菊芳, 赵睿, 江彬, 等. 基于大规模天线的多用户 MISO 下行链路频谱效率分析[J]. 通信学报, 2014, 35(2): 125-136.

LI J F, ZHAO R, JIANG B, et al. Analysis of spectral efficiency on multiuser MISO downlink based on large-scale antennas[J]. Journal on Communications, 2014, 35(2): 125-136.

[12] 胡莹, 冀保峰, 黄永明, 等. 基于上行多用户大规模MIMO系统能效优化算法[J]. 通信学报, 2015, 36(1): 1-7.

HU Y, JI B F, HUANG Y M, et al. Energy-efficient optimal algorithm based on uplink multi-user very large MIMO system[J]. Journal on Communications, 2015, 36(1): 1-7.

[13] CHAN P W C, LO E S, WANG R R, et al. The evolution path of 4G networks: FDD or TDD?[J]. IEEE Communications Magazine, 2006, 44(12): 42-50.

[14] CHEN J, LAU V K N. Two-tier precoding for FDD multi-cell massive MIMO time-varying interference networks[J]. IEEE Journal on Selected Areas in Communications, 2014, 32(6): 1230-1238.

[15] XU Y, YUE G, MAO S. User grouping for massive MIMO in FDD systems: New design methods and analysis[J]. IEEE Access, 2014, 2: 947-959.

[16] ADHIKARY A, NAM J, AHN J Y, et al. Joint spatial division and multiplexing: the large-scale array regime [J]. IEEE Transactions on Information Theory, 2013, 59(10): 6441-6463.

[17] DAI L, GAO Z, WANG Z. Joint channel estimation and feedback with low overhead for FDD massive MIMO systems[C]// 2015 IEEE/CIC International Conference on Communications in China (ICCC). 2015: 1-6.

[18] WANG D, WANG X, YANG X, et al. Design of downlink training sequences for FDD massive MIMO systems[C]//2015 IEEE International Conference on Communications. 2015: 4570-4575.

[19] SO J, KIM D, LEE Y, et al. Pilot signal design for massive MIMO systems: a received signal-to-noise-ratio-based approach[J]. IEEE Signal Processing Letters, 2015, 22(5): 549-553.

[20] ZHAO P, WANG Z, SUN C. Angular domain pilot design and channel estimation for FDD massive MIMO networks[C]//2017 IEEE International Conference on Communications (ICC). 2017: 1-6.

[21] WANG Y, LI C, HUANG Y, et al. Energy-efficient optimization for downlink massive MIMO FDD systems with transmit-side channel correlation[J]. IEEE Transactions on Vehicular Technology, 2016, 65(9): 7228-7243.

[22] BJÖRNSON E, HOYDIS J, KOUNTOURIS M, et al. Massive MIMO systems with non-ideal hardware: Energy efficiency, estimation, and capacity limits [J]. IEEE Transactions on Information Theory, 2014, 60 (11): 7112-7139.

[23] TRUONG K T, HEATH R W. Effects of channel aging in massive MIMO systems [J]. Journal of Communications and Networks, 2013, 15(4): 338-351.

[24] BJÖRNSON E, SANGUINETTI L, HOYDIS J, et al. Optimal design of energy-efficient multi-user MIMO systems: is massive MIMO the answer?[J]. IEEE Transactions on Wireless Communications, 2015, 14(6): 3059-3075.

Effects and optimization of pilot sequence length on rate in multiuser massive MIMO FDD system

WANG Yi1,2, MA Pengge1, HUANG Kaizhi2, LI Chunguo3, HUANG Yongming3, YANG Lyuxi3

1. School of Electronics and Communication Engineering, Zhengzhou University of Aeronautics, Zhengzhou 450046, China 2. National Digital Switching System Engineering and Technological Research Center, Zhengzhou 450002, China 3. School of Information Science and Engineering, Southeast University, Nanjing 210096, China

The effect of pilot sequence length on the asymptotic performance of the ergodic rate was investigated for the multiuser massive multiple-input multiple-output (MIMO) frequency division duplexing (FDD) downlink system. Firstly, the analytical expression of the ergodic rate was derived by using the principle of deterministic equivalence, based on which, it was discovered from the analytical results in two-fold that the normalized pilot sequence length (defined as the pilot sequence length divided by the number of BS antennas) tends to zero yet the rate was guaranteed to grow large without limit as long as the BS antenna number continues to increase, the rate saturates to a certain level if the BS antenna number becomes large with fixed pilot sequence length. Moreover, the pilot sequence length was optimized based on the sum-rate maximization within a finite channel coherence time, and a closed-form solution was deduced under a special correlated channel by means of Lambert W function. Simulation results validate the correctness of the theoretical analysis results and verify the effectiveness of the proposed closed-form solution of the optimal pilot sequence length.

massive MIMO, FDD, pilot sequence length, downlink rate, asymptotic analysis

TN92

A

2017−11−27；

2018−05−25

王毅，yiwang@zua.edu.cn

国家自然科学基金资助项目（No.61372101, No.61671144, No.61701538, No.U1404615）；中央军委十三五预研基金资助项目（No.6140311030207）；中国博士后科学基金资助项目（No.2018M633733）；河南省高校科技创新团队支持计划基金资助项目（No.17IRTSTHN014）；河南省科技攻关计划基金资助项目（No.182102210449）；河南省高等学校重点科研基金资助项目（No.19A510024）；江苏省高校自然科学研究面上项目（No.16KJB510008）

10.11959/j.issn.1000−436x.2018120

The National Natural Science Foundation of China (No.61372101, No.61671144, No.61701538, No. U1404615), Central Military Commission Advance Research Fund (No.6140311030207), China Postdoctoral Science Foundation Project (No.2018M633733), The Science and Technology Innovation Teams of Henan Province for Colleges and Universities (No.17IRTSTHN014), The Scientific and Technological Key Project of Henan Province (No.182102210449), The Key Project of Henan Province for Colleges and Universities (No.19A510024), The Natural Science Research Project of Jiangsu Province for Colleges and Universities (No.16KJB510008)

王毅（1984−），男，河南三门峡人，博士，郑州航空工业管理学院讲师，主要研究方向为大规模MIMO、能效通信、无人机辅助通信、物理层安全技术等。

马鹏阁（1976−），男，河南南阳人，博士，郑州航空工业管理学院教授、硕士生导师，主要研究方向为雷达信号处理、激光测距和无人机数据链等。

黄开枝（1973−），女，安徽滁州人，博士，国家数字交换系统工程技术研究中心教授、博士生导师，主要研究方向为无线物理层安全、移动通信网络与信息安全等。

李春国（1983−），男，山东胶州人，博士，东南大学教授、博士生导师，主要研究方向为多天线中继传输技术、短距离宽带极高速无线传输技术等。

黄永明（1977−），男，江苏吴江人，博士，东南大学教授、博士生导师，主要研究方向为MIMO通信信号处理、毫米波通信和新型多址接入技术等。

杨绿溪（1964−），男，安徽桐城人，博士，东南大学教授、博士生导师，主要研究方向为无线通信空时信号处理、协作通信和网络编码等。