基于自助模式的任务定价模型

吴明霞，林琼瑶，解瑞欣，夏志乐

（台州学院 数学与信息工程学院， 浙江 临海 317000）

1 引言

在网络平台中会员接受项目任务，执行并进行反馈从而获得一定报酬。与传统市场调查方式相比，自助服务模式克服了效率低、费用高等缺点，从而使得中国调研业实现大规模、高效率、低成本的大转变。通过制定合理的任务定价，任务发布回馈得到较优的满意度，直接关系到企业长远的经济效应。

由自助服务平台数据反馈发现企业所发布任务的完成程度不高，价格作为其主要影响因素，设计定价的合理性显得尤为重要。查阅相关文献知，影响定价最重要的三大因素为产品成本、消费者、竞争者，其它的因素则来自大环境的影响［1］。本文对现实存在问题进行分析改进，结合实际问题，对影响自助服务平台中任务定价的影响因素进行分析，以提高任务完成程度为主要目标，在旧定价模型的基础上定性得到一更为合理的定价模型。

本文主要考虑以下几个问题：

1.研究任务定价规律，分析任务未完成的原因。

2.设计新的任务定价方案，并和原方案进行比较。

3.考虑实际情况下任务打包发布，修改定价模型，分析其对最终的任务完成情况的影响。

4.为新项目设计新的任务定价方案，并评价该方案的实施效果。

本文的详细数据来源于2017年全国大学生数学建模竞赛B题。

2 问题分析

2.1 问题一分析

利用Spss软件绘制任务分布散点图，区别出不同定价的任务，观察任务分布情况，运用Matlab软件对各类定价任务的分布位置进行拟合，分析得到任务定价与任务位置分布存在的函数关系，再对可能关系到任务未完成的内部因素以及外部因素进行分析。

2.2 问题二分析

任务的重新定价结合考虑会员因素，根据相关经济学文献并结合现实状况得到可能影响任务定价的因素有调查成本、会员密集度、任务密集度、会员信誉值、会员预定限额、会员预定任务开始时间等。运用Spss软件绘制会员与任务分布的散点图，得到不同因素下两者位置分布关系的图形，定性分析各因素对任务定价的影响及程度，借鉴原定价方案中完成度较高的区域，利用线性回归分析各影响因素对定价合理性的影响，从而得到一定量定价方案并结合实际对该方案进行改进。

2.3 问题三分析

由于多个任务较为集中导致竞争压力过大，将任务打包发布，减少有机会选择该任务会员数量以减少竞争压力。利用Spss软件对所给任务进行聚类，得到43个任务包，将所有任务包重新编号，取平均经纬度坐标作任务包坐标。根据问题二所得结论可以得到每个任务包所在位置的价格，该位置任务单价×任务数目即为该任务包价格。分析原定价方案下定价与任务完成度的关系，利用线性回归得出两者定量关系，比较打包前后的任务完成度，分析得到定价模型对最终任务完成情况影响。

2.4 问题四分析

针对新项目任务的定价问题，先将数据进行初步处理，在问题二模型的基础上，利用其解决问题的思路与想法对新项目进行定价，可以得出新项目的定价标准。再根据问题三定价模型对任务完成情况的影响模型来检验该方案的实施效果。

3 模型建立与求解

3.1 问题一

3.1.1 模型建立

1.已知已结束的任务所在经纬度位置、任务定价以及任务完成情况，将相同定价的项目任务归为一类，共得23类项目任务。在APP上市之前任务发布位置以及定价已确定，则不考虑会员因素对该项目定价的影响。目前仅已知的信息为任务点位置信息，则定价规律与任务位置存在一定关系，即：

标价=f（项目位置）

利用Matlab软件对每一类项目任务点的分布位置进行拟合，生成拟合曲线以及相应函数式。各类项目任务在平面坐标系中的相对位置拟合情况如图1。

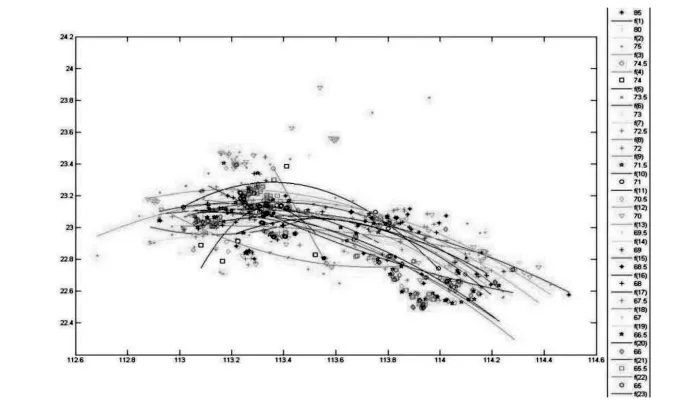
图1 各类项目任务位置拟合曲线

2.考虑任务点完成与周边环境的关系，将这些点的经纬度坐标导入BDP软件，在地图上标注该些点位置，部分任务点位置分布如图2所示。

图2 任务点位置分布

3.1.2 模型结论

1.将任务经纬度坐标考虑在平面坐标内，通过拟合位置曲线，得到定价规律与位置分布的关系如表1，其中x表示任务所在区域。

表1 各类任务区域分布规律函数式

2.分析任务未完成原因，综合得到三个影响因素：定价因素、会员因素以及外界因素。

定价因素：该任务点调查成本高，定价不合理，导致该任务无人问津。

会员因素：（1）会员选择的任务对于其本身来说难以完成，导致任务失败。

（2）由于会员数目远远大于任务数目，部分会员缺乏竞争意识，直接放弃了选择任务的机会，导致遗留了一部分任务没有人去完成。

（3）会员在执行任务过程中发生意外导致任务无法继续执行。

（4）已发布的任务与会员位置关系都比较密集，导致会员用户争相选择，由于预定限额与挑选优先权的原因，部分用户占选多个项目任务，但其并没有能力完成所有项目订单导致个别任务失败。

外界因素：（1）未完成的任务点所在地交通不发达，地形特殊，对于会员来说不易到达，导致这些任务点被会员放弃选择。（2）未完成的任务点所在地地方风俗奇特，导致会员放弃选择。

3.2 问题二

3.2.1 模型建立

利用Spss软件绘制散点图，将相同定价的任务点归为一类在图中加以区别，并用0，1标注已完成与未完成的任务点，作出图像如图3。

图3 任务点分类散点网

观察发现一些区域中发布的项目任务完成程度较高，则在这些区域中，任务定价较为合理，值得借鉴。分析密集度对定价的影响，假如在一块区域中大部分为同一种价位的任务点，则掺在其中的另外价位的任务点可能受到自身调查成本或者其他因素某种程度的影响，从概率的角度说，出现一些异常点是容许的。取同种价位密集的区域，将每一块点集都考虑在0.05×0.05的经纬度坐标面积上，面积为：

S=23.7662 km2

分析各区域内平均会员密集度，平均任务密集度，平均会员信誉值、平均会员预定限额、平均会员预定任务开始时间指标，（预定开始时间用Excel表格转化为数值取平均），得到区域内各项因素指标相对值。采用回归分析法，对各影响因素与任务定价之间的关系进行定量分析。

3.2.2 模型解决

数据导入Spss软件，得到表格如下。

表2 模型摘要

系统输出回归系数如表3。

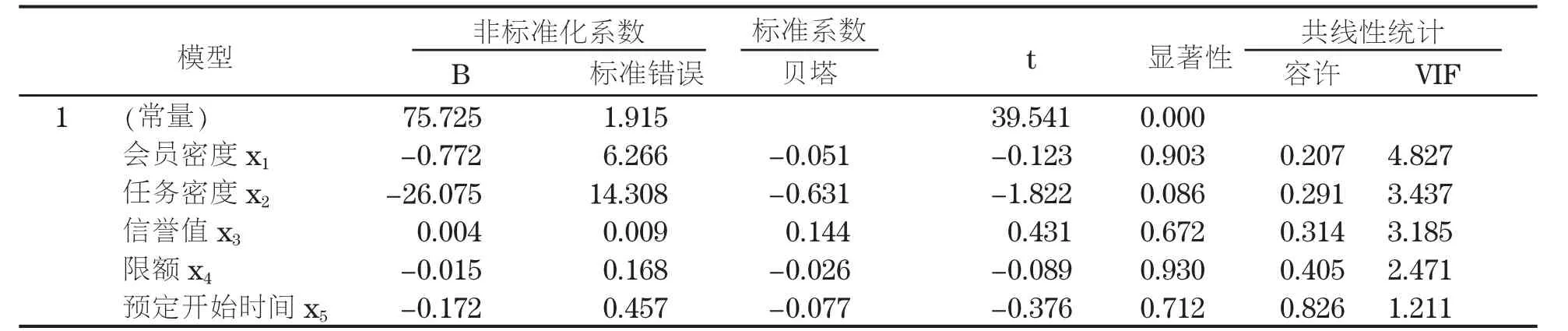
表3 系统输出回归系数

表中显示了模型的偏回归系数（B）、标准误差（Std.Error）常数（Constant）标准化偏回归系数（Beta）回归系数检验的t统计量观测值和相应的概率p值（Sig.）共线性统计量显示了变量的容差（Tolerance）和方差膨胀因子（VIF）.令x1表示会员密度，x2表示任务密度，x3表示信誉值，x4表示限额，x5表示预定开始时间指标，根据模型建立的多元线性回归方程为：

y=75.725-0.772x1-26.075x2+0.004x3-0.015x4-0.172x5

结合实际情况，规定所有结果小于65的任务点统一定价65，所有结果大于85的任务点统一定价85。

3.3 问题三

3.3.1 模型建立

根据用Spss软件对所有任务点进行聚类，得到43个任务包，将其重新进行编号整理，计算包中所有任务点经纬度位置的中心经纬度坐标作为该任务包所在的经纬度位置。

已知确定位置，在周边会员确定的情况下，以该点位置为中心，取定经纬度0.05×0.05大小的经纬度平面坐标区域，计算该区域内会员密集度x1与任务包密集度x2，以及该区域内的平均信誉值x3、平均预定限额x4、平均预定开始时间指标x5。根据问题二中模型可以得到该区域单位项目任务的合理定价，考虑任务包中任务数目 Ni（i=1，2，…，43），得到任务包定价模型如下：

Y1=（75.725-0.772x1-26.075x2+0.004x3-0.015x4-0.172x5）×Ni，i=1，2，…，43

考虑定价对最终任务完成程序的影响，比较打包前后任务完成百分比。分析定价与任务完成程度的关系，整理数据如表4。

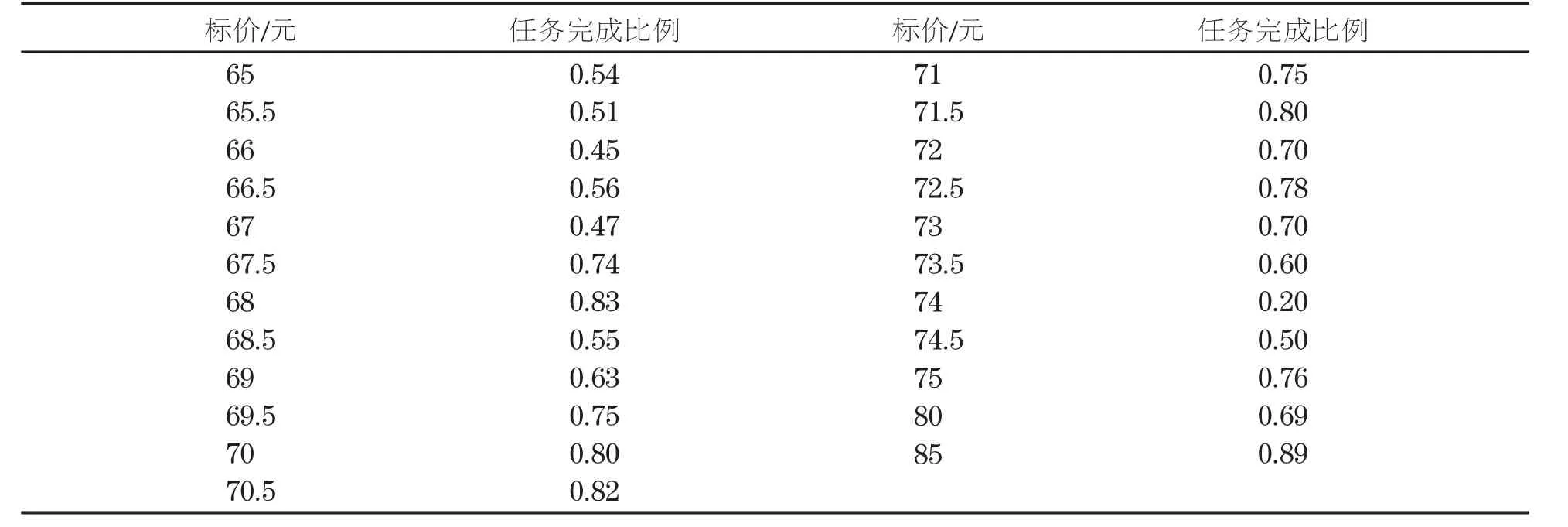
表4 任务完成度与标价关系

利用线性回归定量得出两者关系。

3.3.2 模型解决

定价与任务完成度线性回归方程如下Pi=-0.104+0.011Yii=1，2，…，43

在任务包、会员的位置关系已确定情况下，可以根据公式给任务包定价，在定价取定情况下，再由公式可以计算任务包任务执行程度Pi，则总体任务完成情况计算公式如下:

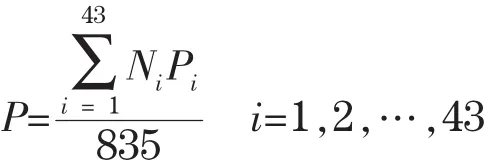
比较打包前后任务完成度以及可采取的改进措施：

当P前＞P后，打包后降低任务完成度，取消对这些任务点打包。

当P前＜P后，打包后提高任务完成度，打包可取。

当P前=P后，打包不影响任务完成度，打包不影响任务完成度。

3.4 问题四

3.4.1 模型建立

对于新项目的经纬度数据，作出其C级任务的位置（实心点）以及会员的位置（圆圈）散点图。取其中特定密集的区域进行放大并加入网格线，观察分布情况，随机取一个任务点，根据公式计算得出它在该经纬度区域内会员密度、任务密度、信誉值、限额、预定开始时间指标，可以得到效果图，见图4，图5。

图5 随机任务点放大图

已得定价公式为

利用问题三中任务完成任务公式

检验任务完成可能性的高低，P值越接近于1，说明可行性越高，即其被完成的越高。

3.4.2 模型结论

通过分析得到新项目的定价是根据任务密度、会员密度、会员的信誉值、会员预订任务开始的时间、会员预订任务的限额以及成本等因素决定的，整体与问题二所得到的定价模型一致。随机取定多组数据的计算得到P值接近于1的居多，占79.87%，因此该方案实施效果较好。

4 模型推广

本模型灵活性高、综合性强，建立在现实基础上真实可靠。模型可以针对不同环境因素进行改进，罗列影响因素，可计算权重进行完善。此模型可以应用于更为宽泛的领域，例如商品促销问题，游戏公司提价原则等。