CT系统的参数标定及反投影成像模型

王 奔，陈娅昵，王吉能，李韶伟

（台州学院 数学与信息工程学院， 浙江 临海 317000）

1 引言

CT成像［1，2，3］是利用X射线对人体进行扫描，获取人体信息，已成为医学诊断中一种重要的手段。其基本原理是：当X射线穿越人体的各个不同的组织器官，由于不同介质的吸收系数不同，X射线会有不同的衰减，根据探测器获得的衰减后的X射线能量值，就能得到一张携带人体内部信息的无损图片，进而分析了解得到病人的健康状况。

本文以2017年全国大学生数学建模竞赛A题为背景，利用MATLAB软件对数字矩阵进行正弦函数曲线拟合，从而标定CT系统的参数，进而利用滤波反投影成像技术，将各组探测器接收到的衰减后的X射线能量，转化为物体的实际密度分布信息。

2 正弦函数曲线拟合参数标定模型

首先，我们建立CT系统几何成像的坐标系，确定投影旋转中心（Center of Rotation，COR）的位置坐标。COR的定位直接决定着整个CT系统的精准度，其误差会使CT图像出现伪影［3］而信息失真。

当前，COR的确定方法主要是针对平行束扫描和扇束扫描。针对平行束扫描的COR确定方法包括傅里叶分析法［4］、图像配准法［5］、对称投影相关法［6］、线模扫描法、质心偏移法［7］、迭代法［8］等。而针对扇束扫描的COR确定方法包括迭代法、几何法、正弦图中心法［7］等。

2.1 符号说明

本文涉及到的未知信息较多，为便于表述，本文模型所用的符号说明见表1。

2.2 正弦函数曲线拟合模型

本文基于正弦函数曲线拟合构建了投影旋转中心的计算模型。转换参考系，固定CT系统，视介质旋转，由于椭圆与圆的中心对称性，在旋转中他们的投影点呈简谐运动。X射线投射的角度是以一定角度步长旋转的。我们计算得到探测器单元之间的距离，并证明角度变化是均匀的，见图1。

表1 符号及其说明

2.3 探测器单元间距

图1 简谐运动示意图Fig.1 A diagram of Simple harmonic motion

以X射线的发射器和探测器作为参考系，小圆绕一点顺时针旋转，而旋转不改变小圆在探测器上的投影长度和投影质量。由于探测器单元之间存在间隔，所以接收到小圆信息的探测器数量会发生改变。直径为D的小圆，单元数可能为m或m+1，该圆直径必定大于m+1个单元距离。

对赛题附件二①指2017年全国大学生数学建模竞赛A题之附件二，文中后面所提到的附件及附件三，附件五均出自于此竞赛题目。的数据处理，筛选出能够完整反应小圆信息的数据，即取射线方向第1～13与第109～180，在这85条信息中提取小圆信息，滤掉椭圆的信息。筛选出吸收强度最大的点。该点位于第135组X射线方向下，第62个单元，吸收率大小为14.1796。

设小圆直径吸收率为D'（D'≈14.1796）。以第一组X射线方向为例，各单元光束到圆心距离为

取圆心两边距离圆心最远的两点，利用距离与直径的比值计算相邻两个射线的距离，即取第n1个与第n2个，得到小圆直径与相邻两个射线单元距离ds的关系式

通过上述方法可对每一个射线方向，求解相邻两个X射线单元距离ds，可得ds≈0.2768 mm，偏差小于 6.4220×10-7mm，这与评阅意见［14］结果相符。

2.4 小圆中心位置与X射线方向关系

由于小圆中心在x轴上作简谐运动，因此小圆中心与发射器角度α1满足正弦函数关系

可见，对于第 n 个方向的 α1，都有唯一的 x1与之对应，x1由d0，n1与d0，n2确定，即

对α1和x1进行正弦函数曲线拟合，可得到小圆中心在x轴上的位置与发射器方向之间的关系。

2.5 椭圆中心位置与X射线方向关系

同理，椭圆中心在x轴上作简谐运动，因此椭圆中心与发射器角度α2的关系可表示为

此处，我们提取附件中的椭圆边界数据（分上边界和下边界），分别拟合得到上边界与下边界的正弦表达式。取上下边界的中点作为椭圆中心在第x0组方向上的位置。注：式（3）中的A1的物理意义是小圆中心位置的振幅，几何意义是小圆中心到旋转中心的距离。式（5）中的A2的物理意义是椭圆中心位置的振幅，几何意义是椭圆中心到旋转中心的距离。

2.6 确定旋转中心在正方形上的位置

由于已知小圆中心与椭圆中心的距离为45.0000 mm，故小圆中心、椭圆中心与旋转中心可构成一个三角形。

以正方形模板中心为原点，平行于底边为x轴，建立平面直角坐标系，得到椭圆中心的坐标为（0，0），小圆中心的坐标为（45，0）。

设旋转中心的坐标为（x，y），可以得到二元二次方程组

求解上式可得两个旋转中心坐标（40.7290，56.2650）和（40.7290，43.7350）。

小圆与第一组方向的角度为-0.9380，椭圆与第一组方向的角度为-0.4428。说明在旋转方向上小圆与第一组方向角度大于椭圆，又因为每个探测器绕固定点逆时针旋转，所以确定旋转中心坐标为（40.7290，56.2650）。

2.7 射线方向

X射线发射器的方向共有180个，方向角度以等步长旋转。取实际的x1，x2代入

对比（7）式和（8）式，小圆的第1个发射器的角度为-0.9380，第180个发射器的角度为2.1756；椭圆的第1个发射器的角度为-0.4421，第180个发射器的角度为2.6582。分别做差，发现旋转角度的变化为179.1834°.

以第一组X射线方向为例见图2，∠1=arcsin0.4271=25.2825°，∠2=arcsin∠1+∠2=60.3319°.这与评阅意见［14］结果相符。

图2 第一组方向的计算Fig.2 The calculation of the first set of directions

3 平行束滤波反投影重建算法

3.1 重建算法物理基础

重建算法在CT技术的发展中占举足轻重的地位。其实质是通过扫描介质获取衰减系数［10］线积分数据为基础。通过运算解出矩阵中的像素值重构图形。CT重建算法基本分为如下两类：

（1）傅里叶变换重建算法，以Radon变换理论为基础，先连续化解析处理，后离散化处理；

（2）滤波反投影重建算法［11］，将每一个角度下的投影进行卷积处理，改善伪影。

以下我们采用滤波反投影重建算法实现CT图形重建。

在X射线穿过物体时，由Beer定理可知，在均匀材料中，X射线强度衰减满足公式

3.2 Radon变换

Radon变换［12］从理论上证明了射线投影就是二维分布函数在一定角度下的线积分，设二维平面内的直线L与X夹角为φ，原点到直线L的垂直距离为s，使用极坐标代换可以进行计算。

若已知待重建图像 f（x，y）=f~（r，θ）沿直线 L 的积分为：

则Radon逆变换为：

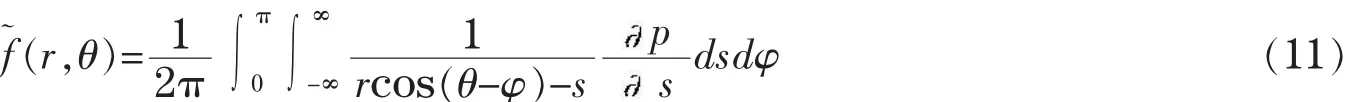
3.3 滤波反投影（FBP）重建［13］算法

设待重建图像为f（x，y），则滤波反投影重建公式：

在此，我们选择合适的滤波器 （如Ram-Lak滤波，Shepp-Logan滤波，Hamming窗以及Hanning窗），把固定角度下的投影进行卷积滤波，得到滤波后的投影，对于每一个固定角度，滤波后的g（xr，φi）反投影满足xr=r cos（θ-φi）的射线上的所有点。将反投影值对所有的角度累加，得到重建后的图像。通过图像重建结果对比，我们发现本题使用Hanning窗进行滤波得到的重建效果最佳。

3.4 反投影过程的线性内插

在平行束反投影过程中，内插运算是非常重要的步骤。点（xi，yj）为图像中某一像素坐标，（xr，m，φm）是在不同坐标下的投影坐标，已知

赛题中，我们观察到 n0dspl＜xr，m＜（n0+1）dspl，反射投影点的选取就需要选择适合的内插方式。一般而言，采用较多的是紧邻内插和线性内插两种方式。本文采用的是效果较好的线性内插。线性插值算法输出的函数值是将实际位置、相邻的射线距离分配不同的权值，再进行线性变换。例如：当ndspl＜xr＜（n+1）dspl时，算法如下表示

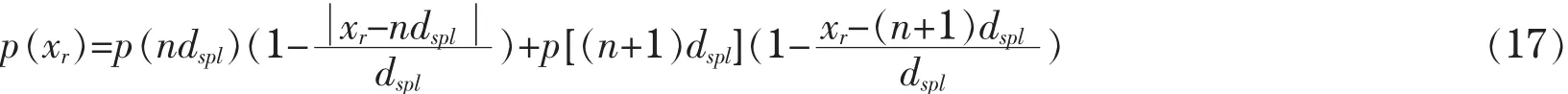
线性内插校正之后，将数据反投影重建起（x，y）处的图像。

假设射线束从1开始计数，一直到N，见图3，给出过像素点的射线位置算法以及它的求和形式，表达如下：

图3 射线示意图Fig.3 A diagram of X-ray

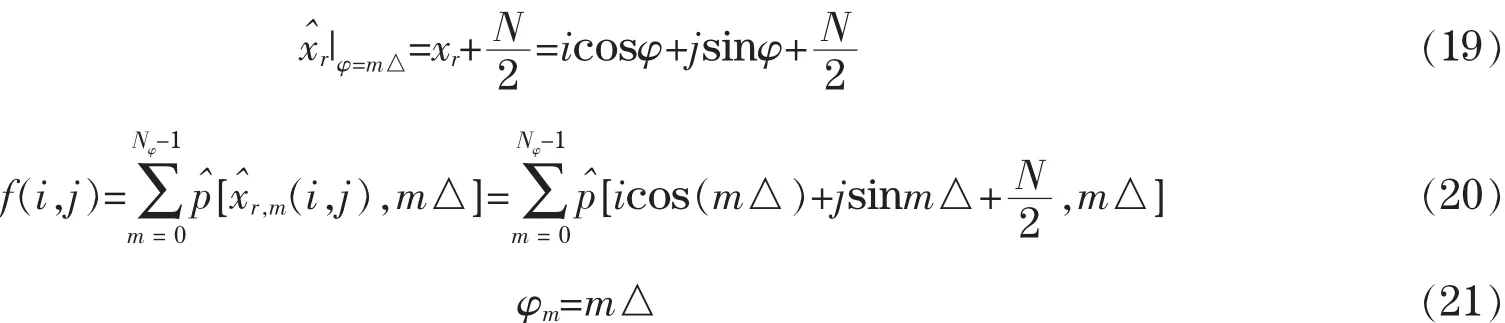
首先确定未知介质的几何形状，再分析确定未知介质的位置、几何形状以及吸收率等信息。

通过上述过程得到的重建图像，明暗区域区分度较大，图像连续性较好，连续区域属性相似，初步判断该未知介质内部较为均匀。要对该介质在正方形托盘中的位置进行定位，首先确定参考系。由iradon变换的特性可知，重建图像所在图片中心即为原始物体在radon变换中的旋转中心。

根据所求得的CT系统旋转中心在正方形托盘中的位置，求得重建图像相对于原始物体的偏移。然而在该CT系统中，进行X射线扫描投影的初始位置并不在正方形托盘正前方，所以偏移之后还要进行一次旋转，即可得到物体在正方形托盘上的准确位置。

从radon变换的数学理论基础出发，切片衰减系数的二维分布函数，由该函数在其定义域内的全部线积分决定，要求解切片衰减系数，进行线积分的逆运算，计算吸收率。图4和图5是依据附件三和附件五的数据重建的图像。

图4 附件三重建图像Fig.4 Annex three reconstruction of images

3.5 正弦拟合位置确定模型的修正

图5 附件五重建图像Fig.5 Annex five reconstruction of images

本文对第一问得出的旋转中心位置、探测器单元距离、X射线的180个方向等参数进行精度与稳定性分析。并优化构造新模板，同时建立起相应的标定模型来改进精度与稳定性。

在第一问的模型中，正弦函数曲线拟合位置确定模型包含了两种不同的算法。关于小圆，由于其图形的简洁特殊性，每一个方向的小圆中心位置可精准确定；关于椭圆，则采用了上下界拟合取中点法，存在着细微的误差。因此制定新的模板，利用两个圆来提高参数标定的精度和稳定性。

4 结束语

本文以2017年全国大学生数学建模竞赛A题为背景，对CT系统的参数标定和投影成像，分别给出了正弦函数曲线拟合模型与平行束滤波反投影成像模型。本文的两个模型具备较高的实用性。