轻薄阵列天线阵面形状调整的作动器布局优化*

刘双荣，周金柱，唐宝富，徐文华

(1. 西安电子科技大学， 陕西 西安 710071； 2. 南京电子技术研究所, 江苏 南京 210039)

引 言

随着通信、国防需求、空间科学的不断发展和变化，对高集成、大口径、轻薄阵列天线的需求越来越迫切。超大口径轻型阵列天线不仅可以收集更多的能量、降低天线重量，同时可以实现多目标探测、跟踪与识别[1]。但大口径、轻型化会导致阵列天线的刚度降低，尤其是天线的服役环境复杂、多变时，天线阵面受到随机、时变的动态载荷的作用而产生结构变形，同时太阳辐射、湿度等也会引起阵面结构材料参数的变化，导致天线阵面变形，使天线服役时可靠性降低[2-3]。为保障阵列天线在复杂、多变环境下工作的可靠性，很多学者将智能结构引入天线阵面的结构设计当中[4-5]。

目前，利用智能结构控制天线阵面形状已受到广泛关注[6-9]。智能结构控制阵面形状主要完成有限量作动器或传感器的布局和作动器调整量的确定。在阵面形状控制中，作动器的位置至关重要，恰当的作动器布置不仅可以实现阵面形状可控，而且所消耗的能量也最少[10]。现阶段已有部分文献对结构控制中作动器的布局进行了研究。文献[11]分析总结了结构控制中作动器优化配置的准则，并结合典型的数值仿真案例进行了分析；文献[12]基于悬臂板模型的最优二次型建立目标函数，利用遗传算法求解黎卡提代数矩阵方程，保证解P的迹最小，以P迹的最小值给出了作动器的最优布局；文献[13]从被控系统的可控性和可观性角度出发，考虑模态截断引起的误差或溢出效应，基于最小控制力建立作动器配置的目标函数，并利用遗传算法给出了最佳作动器配置；文献[10]基于参考输入的特征函数展开，在模态坐标系下依次删除互不相关的模态，选择不同的作动器位置以保证模型可控矩阵的奇异值最大；文献[14]基于模型最小存储能量和最小控制力建立了作动器优化的目标函数，通过混沌粒子群算法给出了最优作动器配置；文献[15]考虑了模型参数的不确定性，通过保证模型的格拉姆矩阵可控的最大化来进行作动器布局优化，并利用遗传算法进行作动器的优化配置；文献[16]通过虚功原理推导了反射面天线变形的均方根误差与作动器输入电压的关系，保证反射面天线变形的均方根误差最小，以此优化配置作动器；文献[17]以输入能量吸收率为优化目标函数，给出了压电作动器抑制结构振动时的最佳作动器配置。通过以上分析可知，已有文献对作动器的优化配置仅单方面考虑模型可控的最大化或精度最小，并未考虑模型可控时作动器布局方式能否满足精度需求，或满足模型期望精度时作动器布局方式是否可以保证模型可控。

1 形状控制的原理

利用智能结构控制轻薄阵列天线阵面形状的原理如图1所示。天线阵面受到复杂、恶劣环境载荷的影响，导致阵面变形，首先，通过分布在阵面上的传感器来监测阵面结构变形；然后，经基于控制算法的控制器产生驱动信号，进而控制作动器补偿阵面结构形状，间接保障天线电性能。

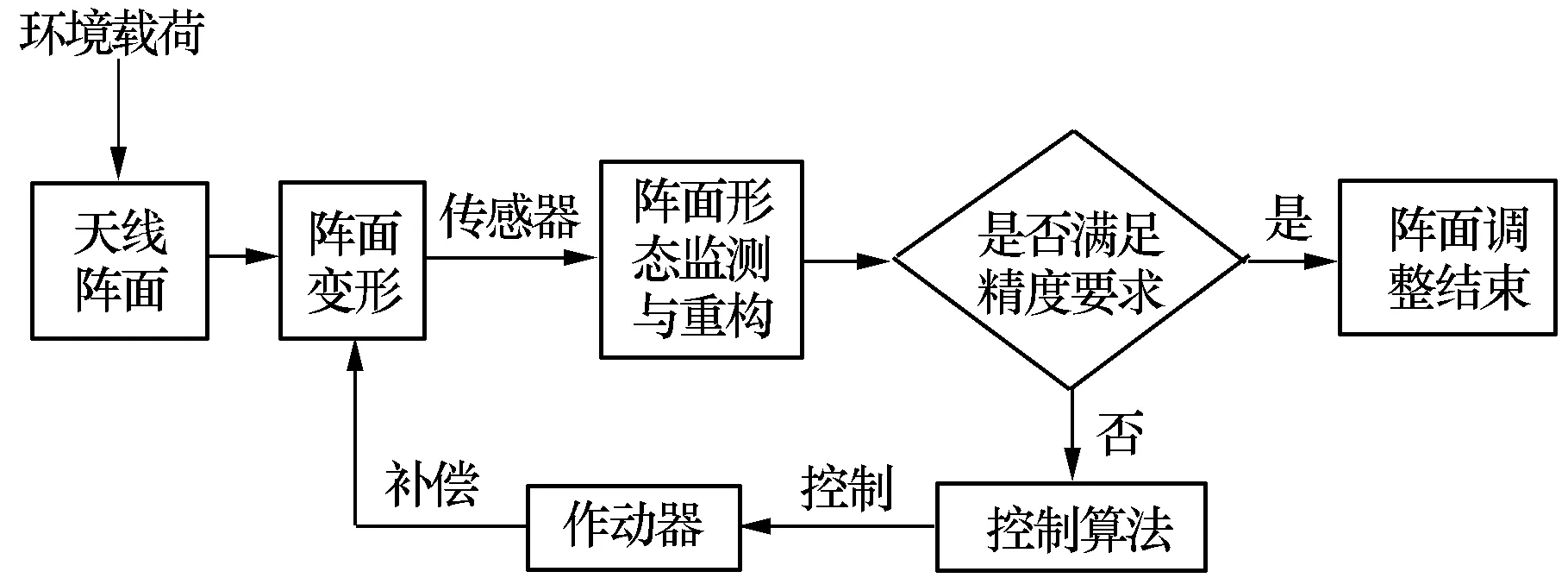
图1 轻薄阵列天线阵面形状补偿原理

利用有限元分析软件对被控轻薄阵列天线的阵面模型进行网格划分，如图2所示。假设作动器布置在阵面有限元模型的第j节点处，可得到作动器在第j节点处施加某一作用力时第i节点的位移[18]：

(1)

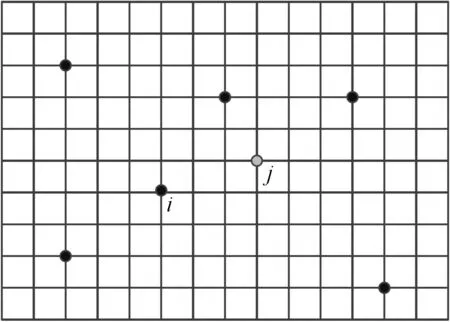
图2 节点间位移关系示意图

用天线阵面有限元模型上所有节点的位移的均方根值来表示阵面变形误差：

(2)

式中：m表示节点数。

令w=Δδ2，知w取最小值时存在：

(3)

由式(1)～式(3)可得：

F=(MN)-1(MG)

(4)

式中：

F=[f1f2…fn]T

当天线阵面作动器位置已知时，可通过式(4)给出保证阵面变形均方根误差最小的任一作动器的输出力大小。由于压电类力矩作动器的输出位移较小，处于微米级，因此，本文主要考虑轻型力作动器，作动器与阵面的连接关系示意见图3。接下来讨论作动器位置的确定方式。

2 作动器布局优化准则

对于连续轻薄阵列天线阵面系统，有下式成立：

(5)

式中：M∈m×m、C∈m×m、K∈m×m分别表示系统的总质量阵、总阻尼阵、总刚度阵；m×1分别为节点位移、速度、加速度列向量；F(t)∈m×1表示节点所受外载荷列向量；T(X)∈m×n、u(t)∈n×1分别为作动器的位置矩阵、输出力向量；X为作动器的位置变量，这里用天线阵面有限元模型的单元节点编号表示作动器位置；n为作动器数目；m为节点数。

对矩阵T(X)作如下定义：

T(X)=[T1(X1)T2(X2) …Tn(Xn)]m×n

(6)

式中：Xi表示第i作动器的节点编号；Ti(Xi)∈m×1表示第i作动器所在位置列向量。

Ti(Xi)=[T1i(Xi)T2i(Xi) …Tji(Xi)]T

(7)

式中：i=1,2,…,n；j=1,2,…,m。

(8)

式中：1表示布置作动器；0表示无作动器。

假设天线阵面系统无阻尼，利用经典模态分析方法，天线阵面的固有频率ωi(i=1,2,…,m)和振型矩阵Φ∈m×k(k表示截断模态数)可以很方便地获得。通常，存在ΦTMΦ=I∈m×m，ΦTKΦ=Λ∈m×m，其中，同时，根据模态叠加原理，将式(5)用状态空间方程表示为：

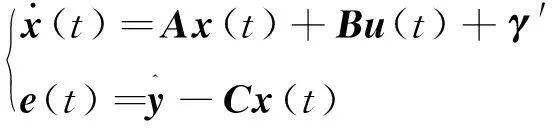
(9)

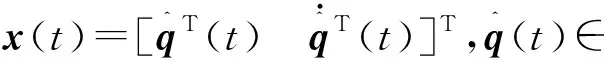
为保证作动器补偿后阵面变形均方根误差最小，同时作动器输出能量最小，则对于连续天线阵面系统有：

(10)

式中：Q、R分别表示输出权系数对称矩阵和控制权系数对称矩阵，且Q为半正定矩阵，R为正定矩阵；t0、tf分别表示有限时间控制器的时间上、下界。

公式(10)的最优解为：

(11)

式中：x0表示状态向量x(t)的初始值；P、δ、φ见式(12)～式(14)。

(12)

(13)

(14)

式(11)～式(14)中P为正定对称矩阵的充分条件为：Q=Im×m且(A,B)完全能控。

根据式(9)可知，变量X≠0时，总有矩阵M满秩，这里选取Q=Im×m，证明如下：

∵M= [BAB…A2k-1B]=

而元素ΦTT(X)和-ΛΦTT(X)都非零，因此rank(M)=2k，即矩阵M满秩，(A,B)完全能控。

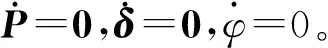
▽J*(x0)=Px0-δ=0

(15)

时，J*最小。解得x0=P-1δ。

因此公式(10)的最优解为：

(16)

其中：

在形状控制中，作动器的位置是保证被控系统在控制力的作用下获得最佳精度或性能的关键，而如何布置作动器的位置是一类组合优化问题。根据上述分析，可得如下的作动器布置的优化模型：

Findh=(x1,x2,…,xn,y1,y2,…,yn)

(17)

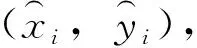
3 遗传算法

遗传算法是1975年美国密歇根大学的Holland教授提出的一种仿生算法，即模拟生物进化的算法。它是从一个初始种群出发，不断重复执行选择、交叉和变异的过程，使种群变化越来越接近某一目标。此类算法可以有效地解决0-1组合优化问题，因此本文选取遗传算法来确定作动器的布置，以公式(17)中的目标函数作为遗传算法的适应度函数。本优化模型的设计变量为离散整数变量，优化时将其视为连续变量产生种群，然后对种群内各个体进行取整运算，再映射至附近的节点，最后进行适应度评估。

4 数值仿真

为了验证本文优化准则的适用性和有效性，证明该方法可以有效地实现系统的静态形状控制和作动器位置布局，将其应用到悬臂式阵列天线和圆形孔径阵列天线。

4.1 悬臂式阵列天线

目前，机翼天线和星载天线多为悬臂式，此类型天线具有阵面轻薄、服役中易产生结构变形等缺点，且在翼根处表现为小变形，翼尖处表现为大变形。因此本文采用如图4所示的悬臂式天线有限元模型进行应用验证，天线安装方式为悬臂式安装。选取此有限元模型为shell63单元，模型约束方式可根据文献[12]确定。对悬臂式阵列天线有限元模型施加重力载荷和-10 N的部分节点载荷(图4中用红色圆点表示)，产生初始形变量，其中弹性模量为21×1010N/m2，泊松比为0.3，密度为7 810 kg/m3，长宽高分别为500 mm、500 mm、2 mm。选取截断模态数k= 6。与文献[12]中的振型频率作对比，如表1所示。

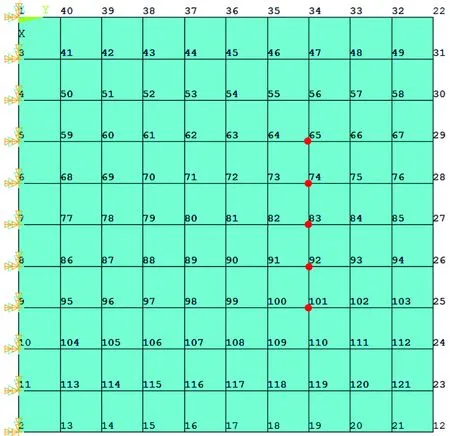
图4 悬臂式阵列天线有限元模型

模态数对比模型/Hz本模型/Hz17.1906.936 9217.90017.045 0343.68242.625 0455.64454.381 0564.57162.125 06109.220108.770 0

通过文中所给的作动器位置优化准则，给定作动器个数n= 6，利用遗传算法进行布局优化，设置作动器间距的最小值d0= 50 mm，遗传算法各参数设置见表2，得到图5所示的结果(黑色实心圆圈代表作动器位置)。根据作动器力计算公式(4)得到调整前后天线阵面变形图，如图6所示。

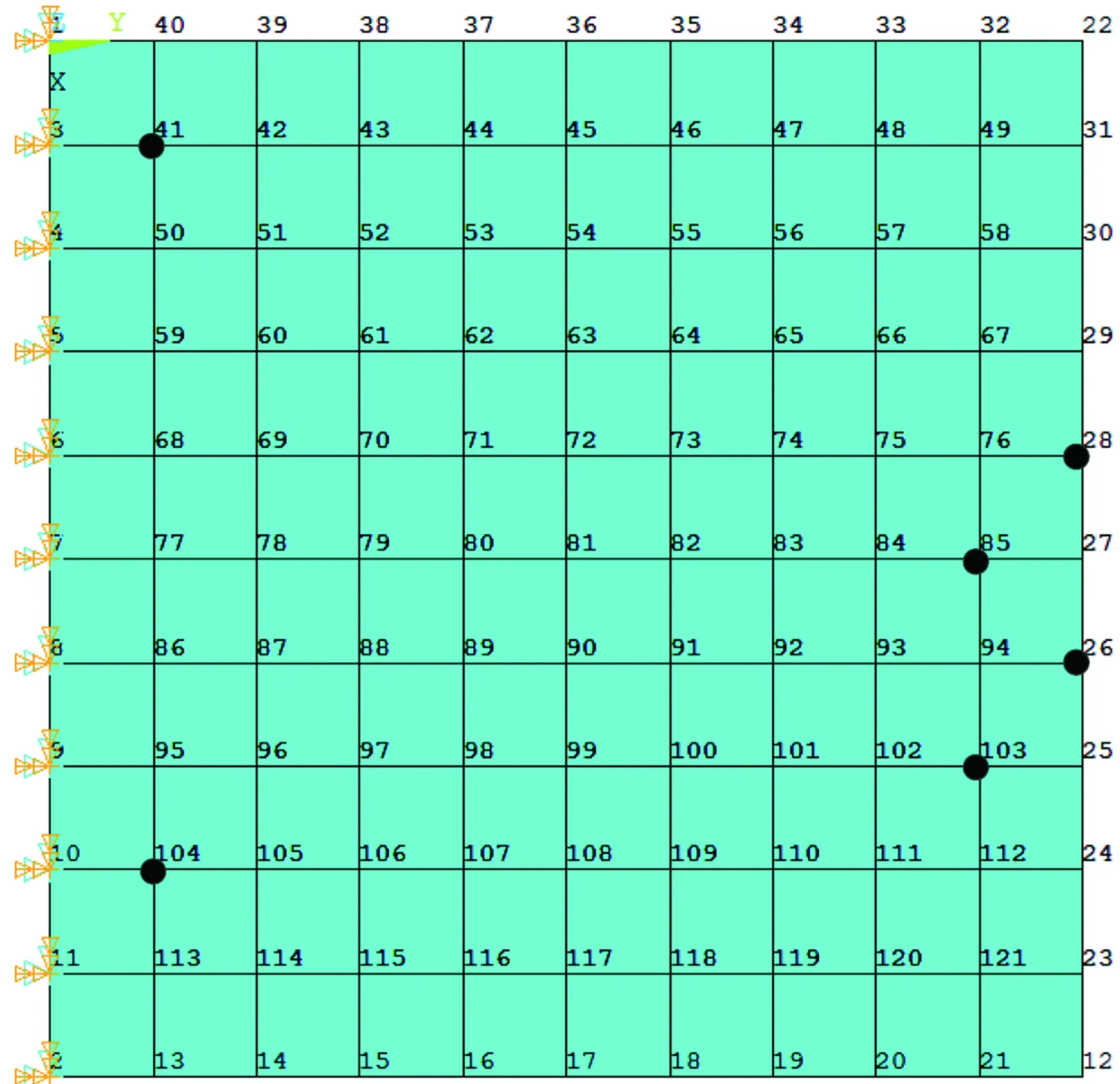
图5 优化后的作动器位置

种群大小交叉概率变异概率遗传代数1000.880.01200

图6 作动器调整前后阵面变形对比图

通过以上数值分析可知，数学模型(17)确定的悬臂式阵列天线模型的作动器布局合理且有效。在此作动器布局下，天线阵面的变形得到调整，且精度提高了85%以上。

4.2 圆形孔径阵列天线

在发射等幅输出情况下，圆形孔径阵列天线的发射最大副瓣低于矩形孔径阵列天线，因此将圆形孔径的阵列天线作为能量传输的发射天线尤为合适，如空间太阳能电站的发射天线。但太空中环境复杂多变，圆形孔径阵列天线不可避免会产生结构变形，导致波束指向发生偏移，因此，需要有效地控制天线阵面变形。

考虑如图7所示的圆形孔径阵列天线的阵面模型，天线辐射单元为贴片单元，阵面背部安装力作动器。支撑方式采用三点支撑，支撑半径参考文献[19]。阵面口径为600 mm，阵面厚度为2 mm，阵面其余参数见表3。

图7 圆形孔径阵列天线阵面有限元模型

弹性模量/(N·m-2)泊松比密度/(kg·m-3)21×10100.37 810

分别取作动器个数n= 8和n= 12进行仿真验证，优化模型见公式(17)，遗传算法各参数设置同前例，仿真验证结果见图8和图9。为方便表示，图中作动器位置统一用红色实心点表示，作动器间距最小值d0= 50 mm。

图8 作动器(n=8)位置示意图

图9 作动器(n=12)位置示意图

圆形孔径阵列天线阵面作动器位置确定后，经阵面形状控制方程(式(4))计算得到阵面变形补偿前后阵面位移云图，如图10所示。分析可知，天线阵面在重力作用下的阵面变形均方根误差为0.098 8 mm，经作动器补偿后阵面变形均方根误差减小了80%以上，尤其是当作动器个数n= 12时，阵面变形均方根误差减小了90%以上。

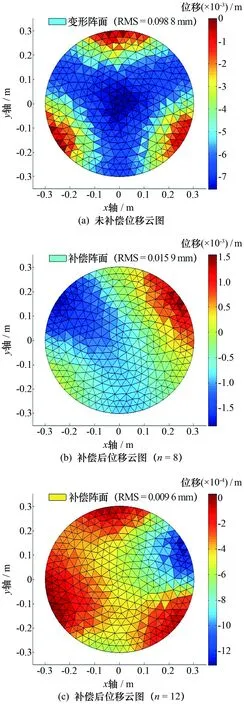
图10 作动器补偿前后位移云图

5 结束语

现阶段，对阵列天线的阵面或反射面天线的面板的主动调控越来越重要，而作动器的布局在天线阵面主动形状控制中占据关键位置，不恰当的作动器位置会导致阵面系统不可控等不确定情况。本文在考虑天线阵面系统可控的基础上，以作动器补偿后阵面变形均方根误差最小，同时所消耗的控制能量最小为目标，给出了作动器布局优化准则。分析结果表明，在该准则下确定的作动器布局可保证轻型阵列天线阵面的变形误差减小80%以上，同时确定了遗传算法对于给定数量的作动器可以有效得到其最佳位置。