花型样条曲线加工代码生成算法

赵福英， 倪俊芳

(苏州大学 机电工程学院， 江苏 苏州 215021)

花样打板系统设计的花型轮廓通常由直线、圆弧、曲线等元素组成，这些曲线大都采用Bezier曲线、NURBS曲线表示[1]。国内研究者[2-4]在B样条应用领域有广泛研究，并取得一定进展，而基于绗缝、提花、针织等自动化设备的复杂花型样条曲线的逼近研究甚少。因为目前大部分数控加工系统只识别直线插补和圆弧插补，所以需要将复杂曲线转换成直线段、圆弧段或者二者混合。

三次样条曲线能够满足曲率半径连续且具有一定的几何意义。当曲线次数越高时，曲线越复杂，应用该曲线加工越困难。三次准均匀B样条曲线具有三次样条曲线的基本特点，且能够支持局部修改，其首末端点与特征多边形相切，方便控制曲线形状；因此，设计花型轮廓时，首先采用三次准均匀B样条曲线进行设计，然后采用插补算法分割曲线。双圆弧逼近三次准均匀B样条的算法，与直线逼近算法比较而言，优点主要包括：保持了原曲线的凹凸性，保证双圆弧位于拟合曲线控制的多边形内部，精度高，可改善加工织物表面品质；与二者混合逼近比较而言，删除了大量的中间点，在给定误差范围内，圆弧段数最少，便于转换成简单的G代码，减少CAD与CAM系统的数据传输，计算效率高。本文提出一种基于误差控制自动分段的双圆弧算法，分析拟合误差ε，利用MatLab计算仿真，最后再将直线、圆弧等花样轮廓离散成均匀的针迹点，生成加工代码，从而加工出复杂的花样图案。

1 双圆弧拟合三次准均匀B样条

1.1 B样条定义

B样条曲线方程[5-7]定义为

(1)

式中：Pi为B样条的控制点坐标；Ni,k(t)为基函数0≤t≤1；i为节点序号，i=0,1,…,n；k为基函数次数。基函数用Cox-deBoor公式表示为

(2)

1.2 双圆弧逼近B样条

图1示出双圆弧曲线逼近B样条曲线示意图。B样条需满足以下要求[8-9]：

1)起始圆弧过曲线P0点，终止圆弧过P1点；

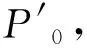
3)分段圆弧在连接处达一阶导数连续；

4)整体逼近的精度在阈值S范围内；

5)所用的圆弧数目应尽可能少。

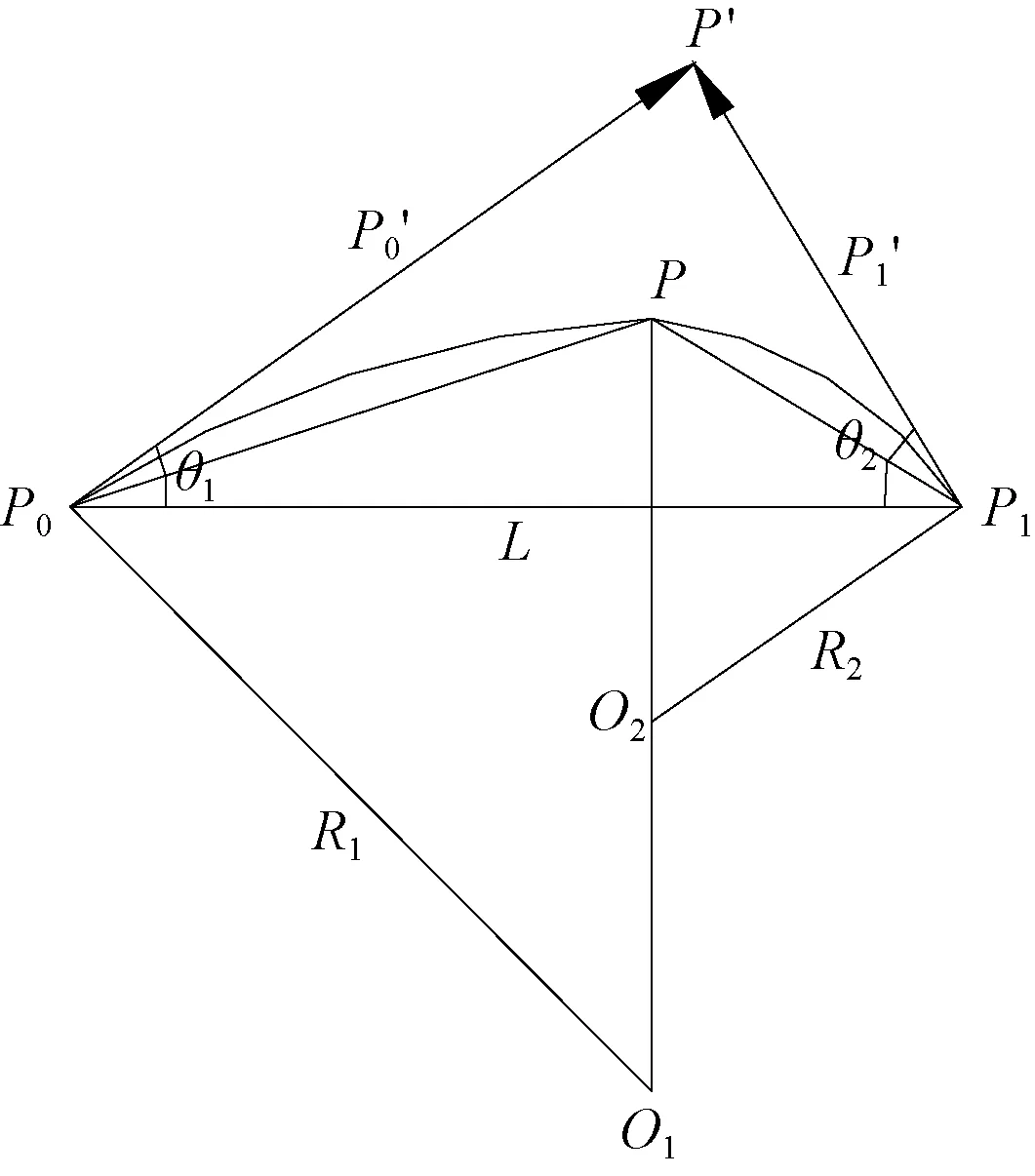
图1 双圆弧逼近B样条Fig.1 Double circular arc approximating B spline

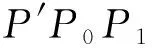
根据图1通过计算可知：

(3)

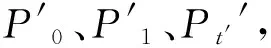
1.3 误差分析

用双圆弧逼近某B样条曲线段{P(t),t∈(0,t′)}或{P(t),t∈(t′,1)}。由图1可知，双圆弧C1和C2均过连接点P，并在与B样条曲线始、末端连线相垂直的直线上。设样条与圆弧的最大逼近误差为ε，则：

(4)

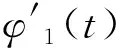
(5)

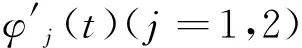
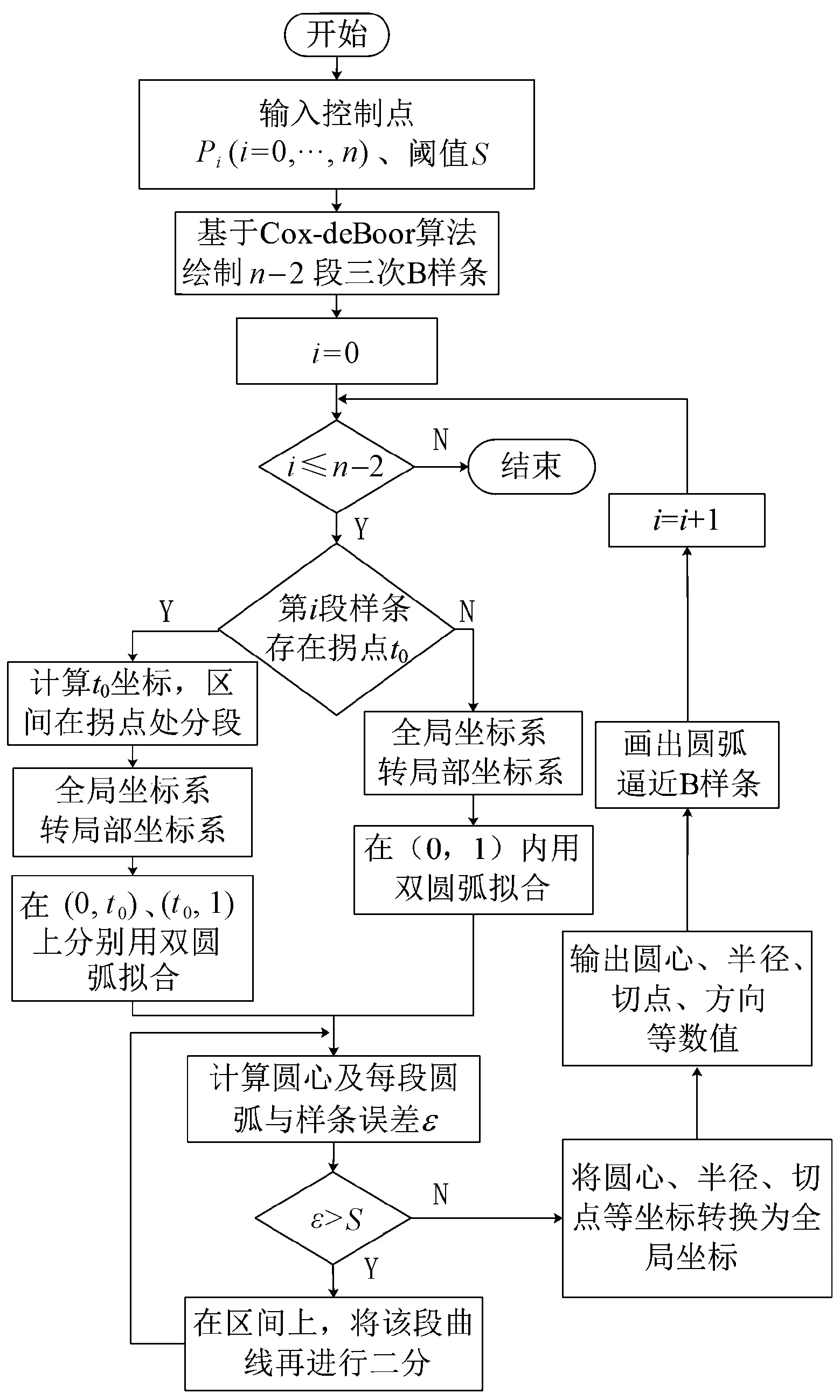
图2 双圆弧逼近三次准均匀B样条算法流程图Fig.2 Flow chart of double arc approximation three quasi uniform B spline algorithm

1.4 MatLab仿真模拟

假设输入样条控制点(1,1)、(2,4)、(3,5)、(4,1)、(6,2)、(5,6)、(2,2)，基于上述算法，利用MatLab编程进行模拟仿真，结果如图3～6所示。

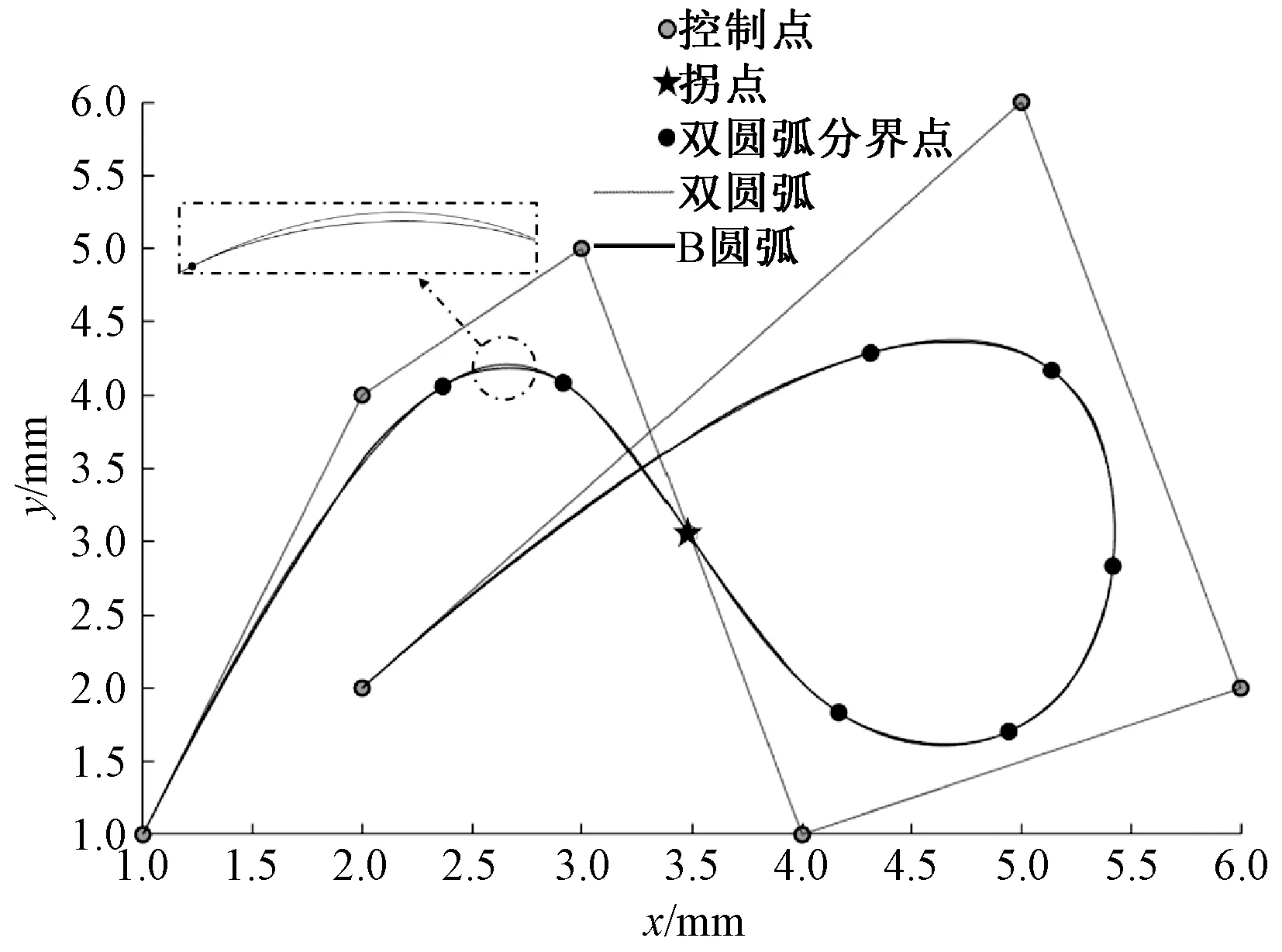
图3 ε=0.1的双圆弧逼近Fig.3 Double arc approximation of ε=0.1

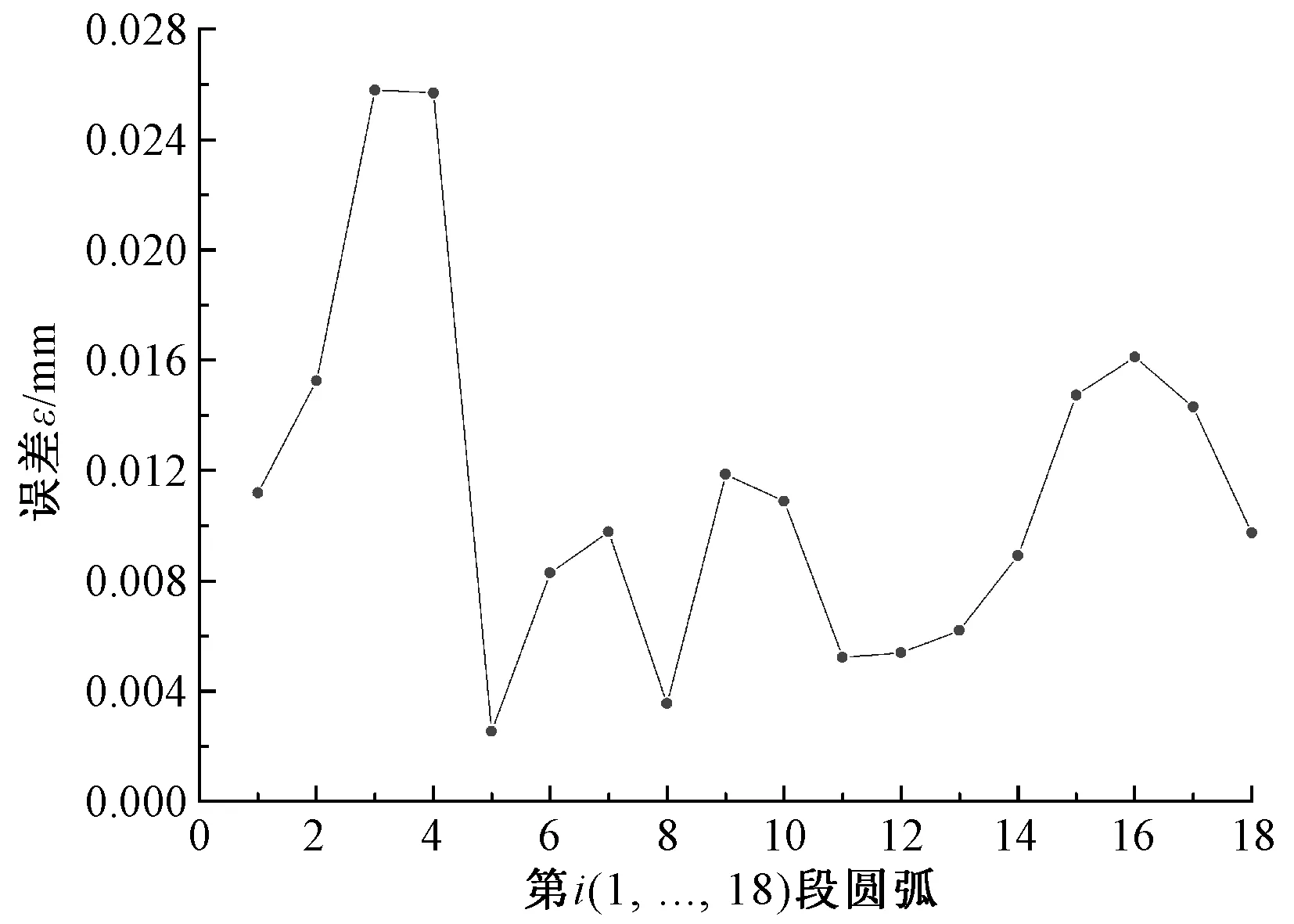
图4 ε=0.1的双圆弧逼近误差分析Fig.4 Double arc approximation error of ε=0.1

图5 ε=0.01的双圆弧逼近Fig.5 Double arc approximation of ε=0.01

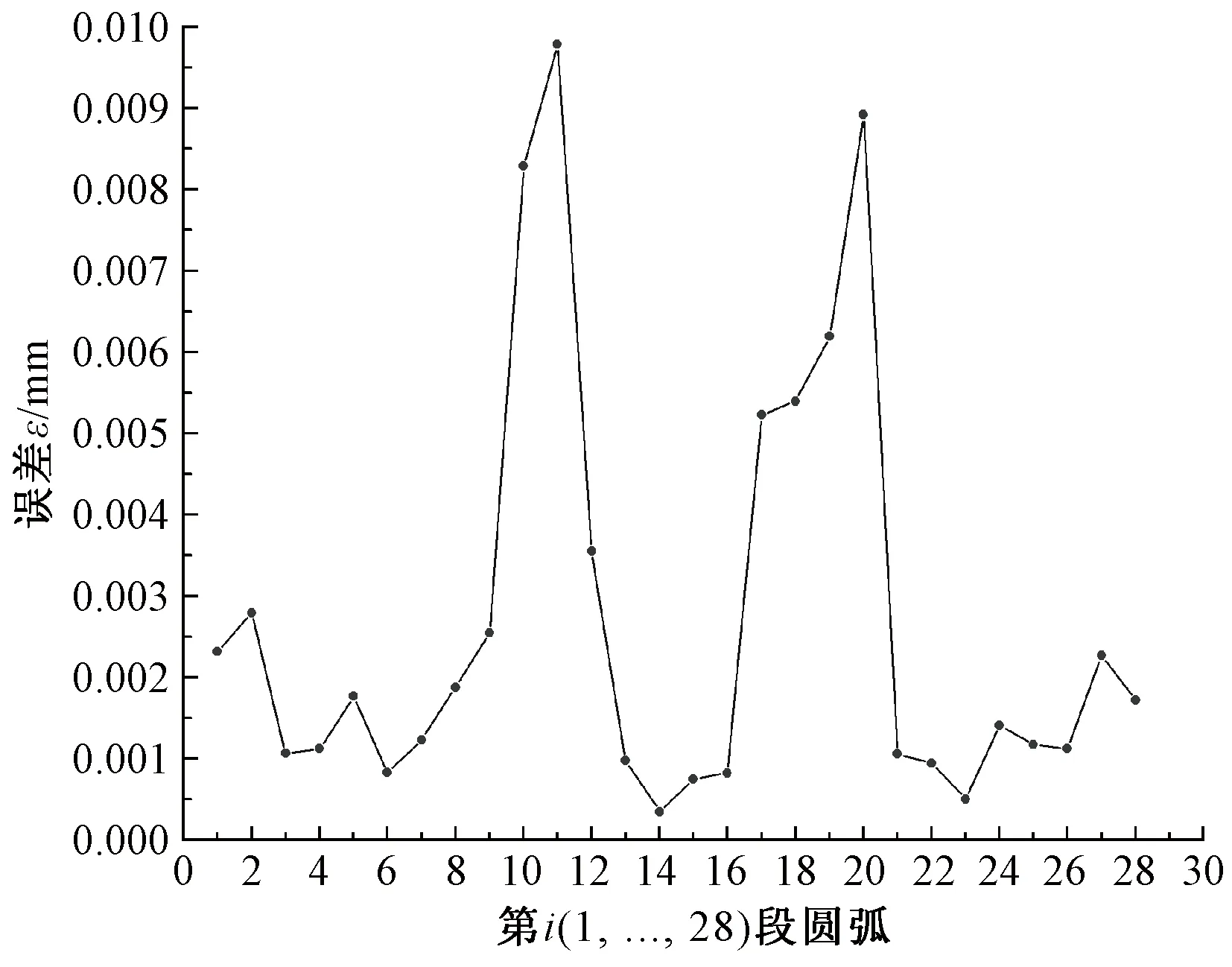
图6 ε=0.01的双圆弧逼近误差分布Fig.6 Double arc approximation error of ε=0.01

2 花样作业图案生成算法

基于多数控制器只能加工直线和圆弧[11]，为了获取高质量的花样数据，解决花样图案针迹点不均匀问题，设计相应的直线和整圆插补算法。

2.1 直线插补算法设计

对于加工代码数据而言，针迹点需分布均匀，且尽可能分布在同一条直线上。设直线起点为A(xa,yb)，终点为B(xb,yb)，长为l，根据步距step，生成其他控制针迹点的算法如下。

1)根据step算出直线花样的针数n。

令m=l/step，r=l%step。其中m，r均为整数。当r≤step/2时，针数n=m；当r>step/2时，针数n=m+1；当m=1且r≤step/2且l>stepmax时，针数n=m+1。

2)根据针数n，将直线等分，计算等分点。

直线起点、终点分别为(xa,ya)、(xb,yb)，令

式中：step_x和step_y取整数；dx和dy取小数。取第1个等分点为(xa+step_x，ya+step_y)，依此类推，第n-1个等分点为(xa+(n-1)×step_x，ya+n-1×step_y)

3)对等分点进行插补。

从第1个等分点到第n个点依次进行插补，当dx=0，dy=0时，算法结束，流程如图7所示。

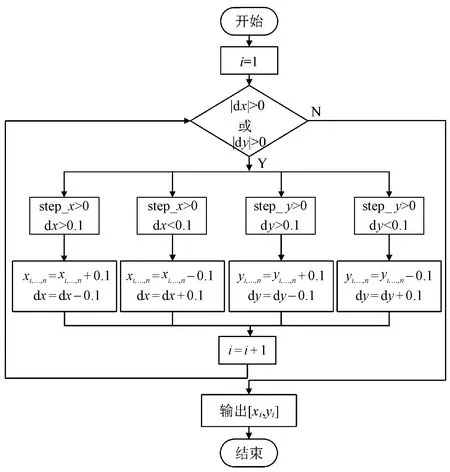
图7 直线插补流程图Fig.7 Flow chart of linear interpolation

2.2 整圆算法设计

已知圆心及半径R，计算出圆上均匀分布的点，步骤如下。

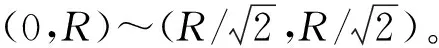
F(Pi)=[(xi+1)2+yi2]-R2

F(Qi)=[(xi+1)2+(yi-1)2]-R2

引入判别式Di=F(Pi)-F(Qi)，判别表达式如下所示：

当i=0,x0=0,y0=R,d0=3-2R;

当Di≥0，选择Pi，xi+1=xi+1，yi+1=yi，di+1=di+4xi+6；

当Di<0，选择Qi，xi+1=xi+1，yi+1=yi-1，di+1=di+4xi-yixi+10。

其算法流程如图8所示。

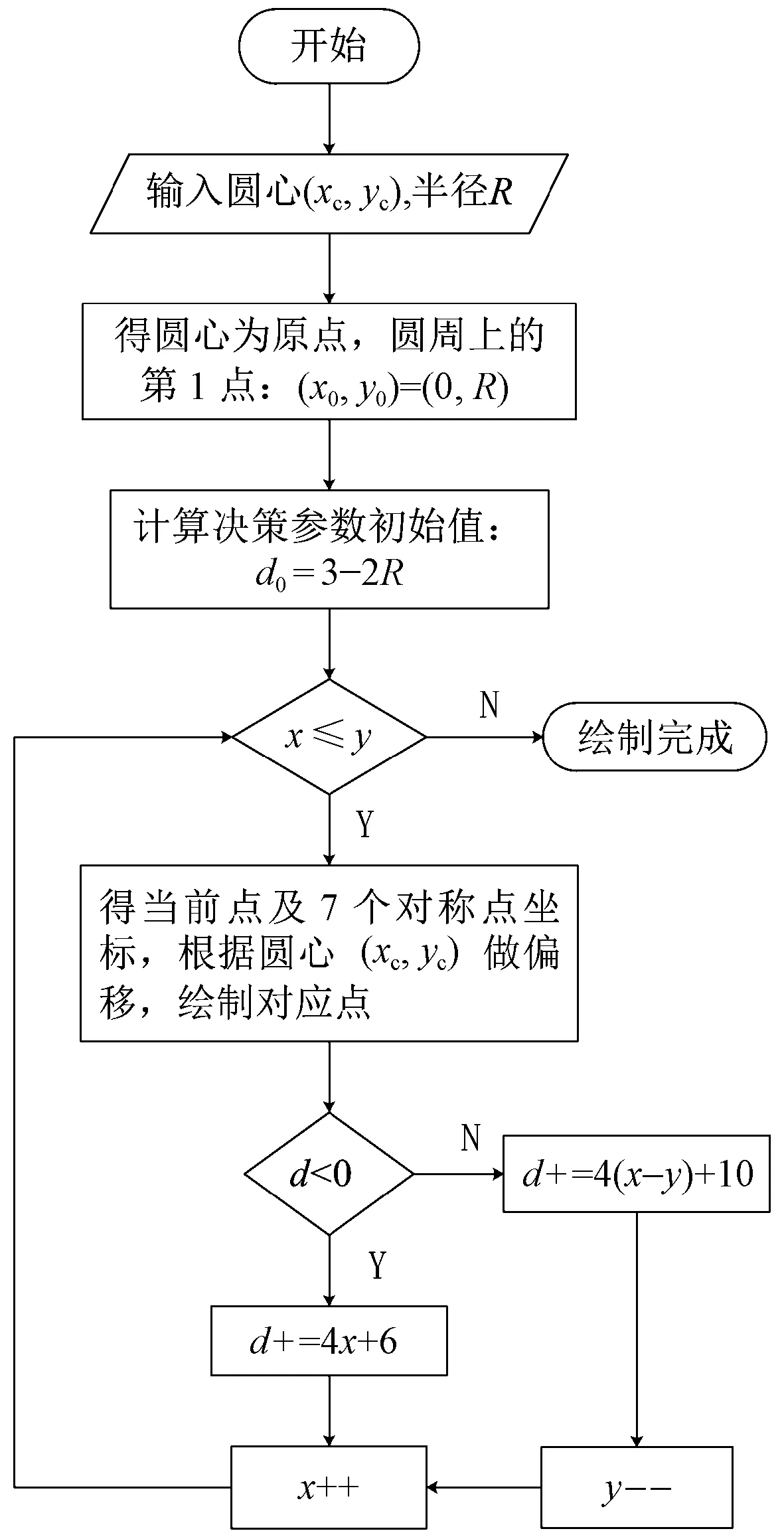
图8 Bresenham算法流程图Fig.8 Bresenham algorithm flow chart

2)根据步距step计算步数n和实际针距ls。

以step为弦长，计算其对应的圆心角α=2arcsinstep/2R，步数n=2π/α，针距ls=2Rsinπ/n。

3)计算圆花样的均匀分布针迹点。

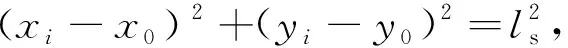
式中：如果dis<0，则第n个针迹点与A点合并。圆弧花样与圆花样生成针迹点算法类似，只要筛选出Bresenham整圆上对应的圆弧区域即可。

3 实 例

3.1 直线花型图案轮廓

输入A(3.7，-11.9)、B(-5.2，10.6)为直线的起点和终点，步距为3.0 mm，根据直线算法，利用MatLab定义函数straight_line([3.7,-11.9],[-5.2,10.6], 3)计算出各个插补点生成加工路径，如图9所示。

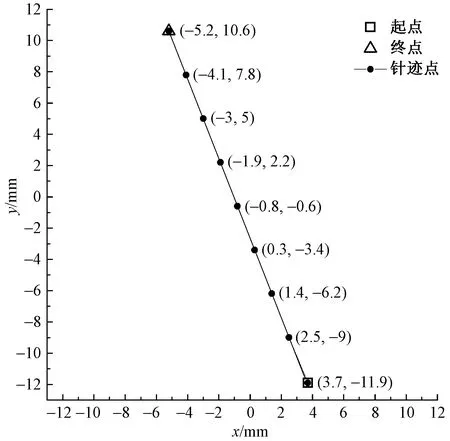
图9 直线花样Fig.9 Straight line pattern

从图9可知，针迹点分布均匀，几乎在同一条直线上，实际针距在3.0 mm左右浮动，加工质量高。

3.2 圆弧花型图案轮廓

输入起点A(x0,y0)，半径R，步距step，方向(a，逆时针；b，顺时针)，根据圆插补算法利用MatLab编程模拟，定义函数circle_bresenham([12.0,16.0],20,3,1)计算出相应的针迹点，生成的花样作业图案如图10所示。由arc_bresenham([12.0,16.0]，[-20,0],20,3,0)生成的均匀针迹点如图11所示。

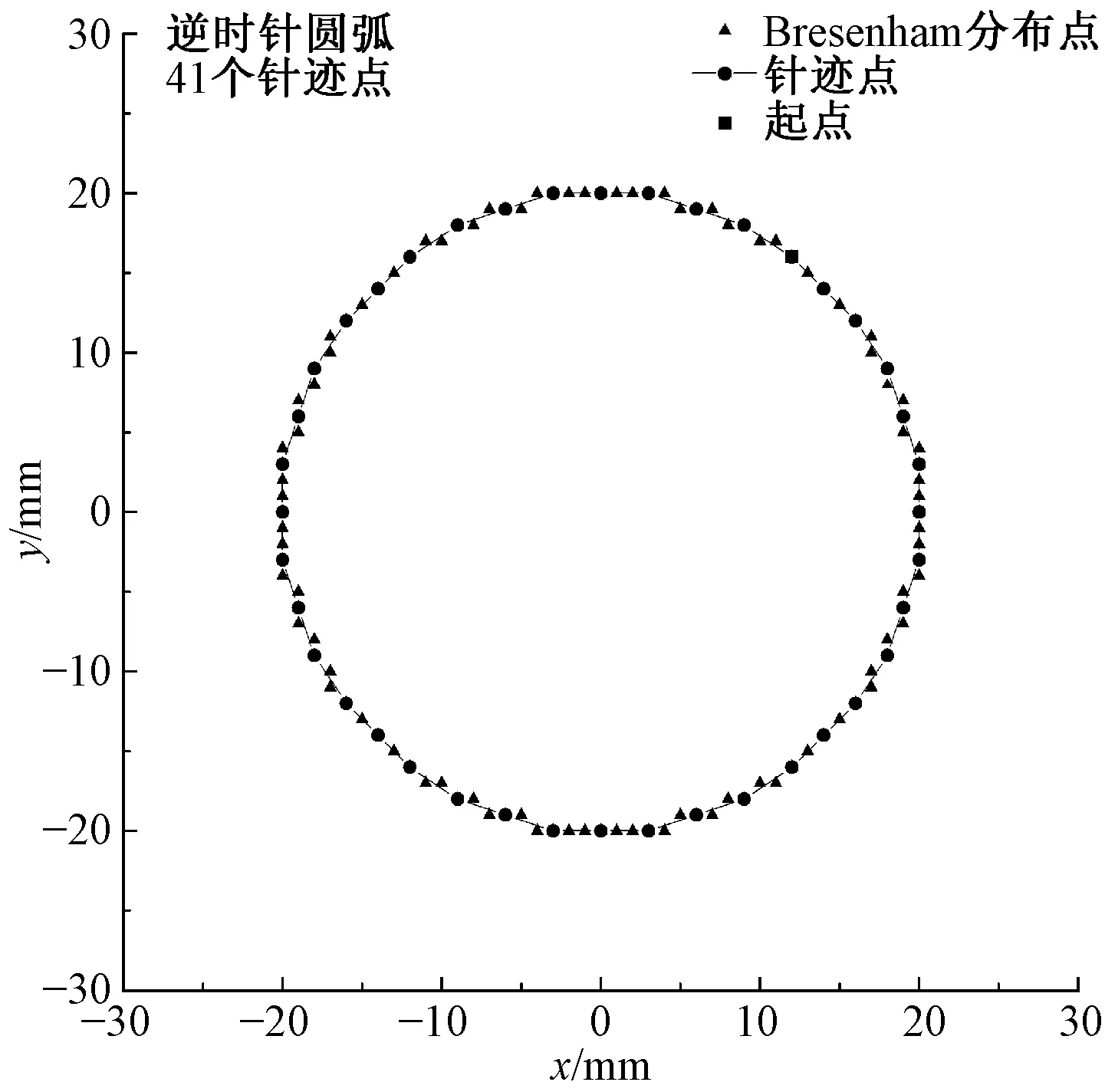
图10 圆花样Fig.10 Round pattern

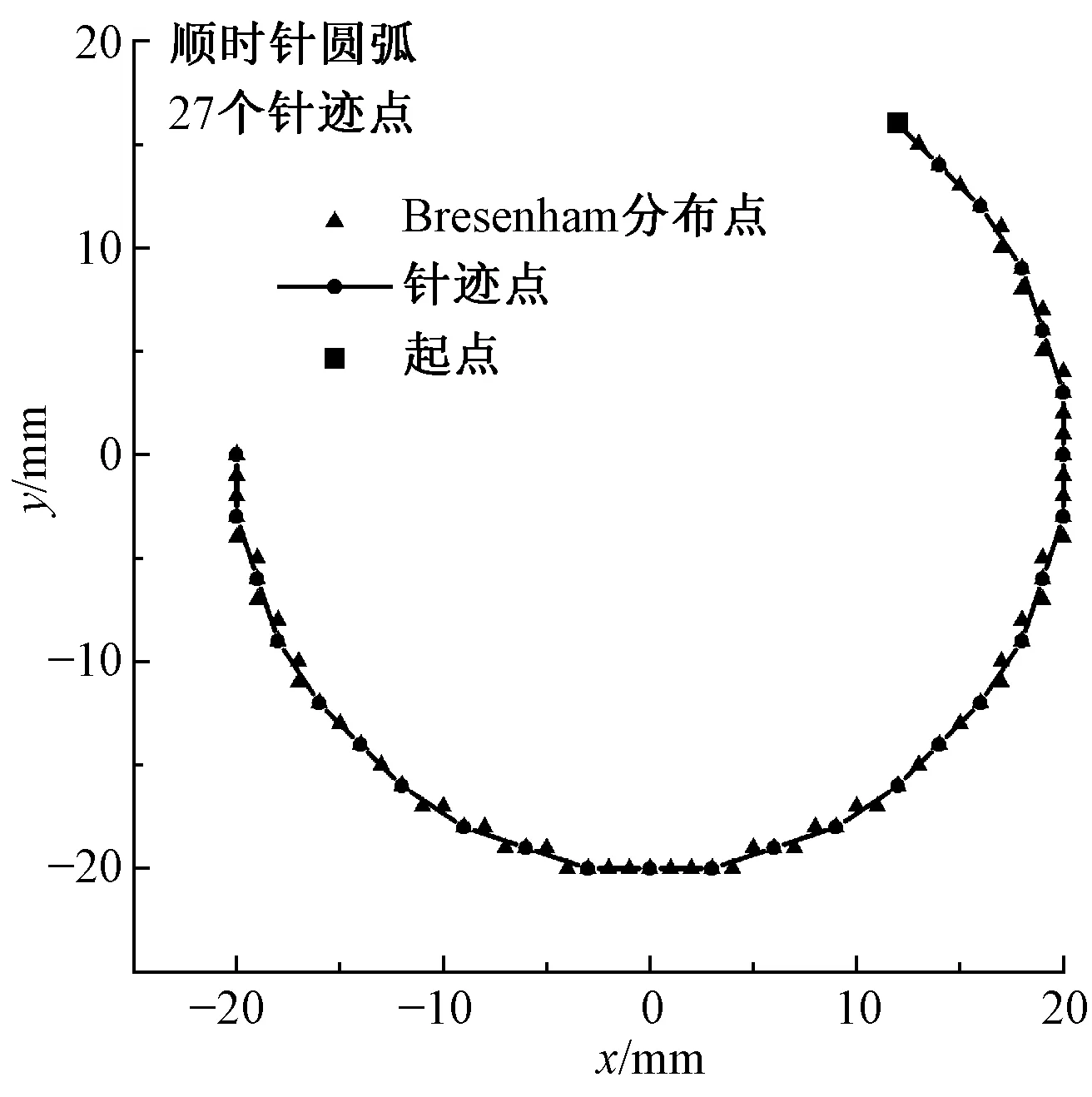
图11 圆弧花样Fig.11 Arc pattern

3.3 机床模拟加工

以C#语言的WinForm为开发工具，采用面向对象的思想设计了花型准备系统。利用双圆弧逼近算法先将含有直线、圆弧、样条曲线的数据文件(如主流格式DST、DXF等)转换成只含有直线和圆弧数据的DAT文件，然后通过GDI+可视化编程将花型矢量图案绘制出来，最后将该文件编译成数控机床可识别的CNC加工程式。DAT文件的分量格式：花样文件有8列数据，每行定义了某一几何线型。其中第1列数据为0、1、2，分别代表直线、圆弧、虚线，-1代表终止程序。第2、3列分别代表该线型的起点横、纵坐标；第4、5列分别代表该线型的终点横、纵坐标；如果该线型为圆弧，则还需要定义圆心的横纵坐标及圆弧走向，分别在第6、7、8列定义。绘制出的花样矢量图如图12所示，数控机床仿真模拟如图13所示。

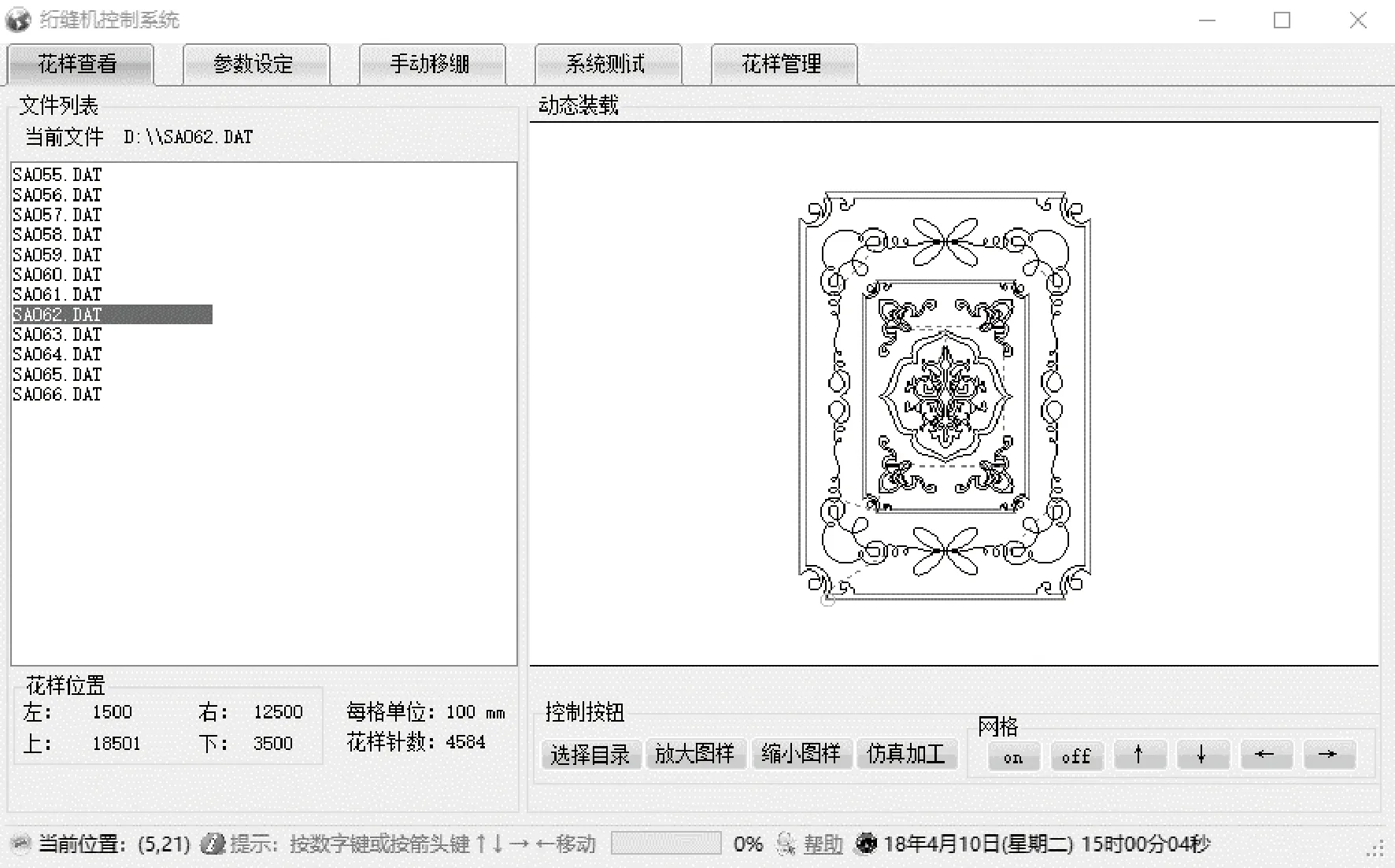
图12 DAT文件的花样矢量图Fig.12 Pattern vectorgraph of DAT file

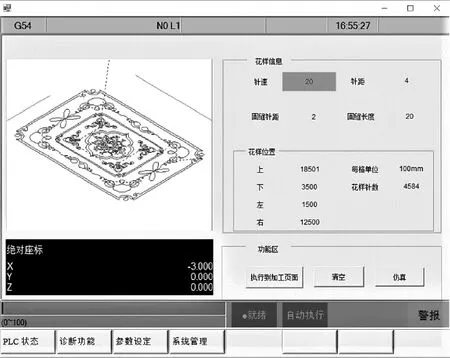
图13 数控机床的模拟仿真图Fig.13 Simulation diagram of CNC machine

图13表明，通过双圆弧逼近算法处理得到的花型图案轮廓光滑、加工质量高，可实现复杂花型的加工。

4 结束语

花型复杂轮廓的逼近是获取高质量的加工数据，解决花样作业图案针迹点不均匀等问题的关键技术。本文基于双圆弧拟合三次准均匀B样条曲线的算法，保证较高的逼近精度，圆弧之间光滑连接保证一阶导数连续。该算法可根据给定阈值，合理规划分段点、双圆弧段数，利用MatLab进行数值模拟，实现了花型针迹点均匀分布。该算法为复杂曲线的数控编程、CAD/CAM系统和自由曲线的等差微段逼近提供参考，并在单针电脑绗缝机、电子花样机等缝制设备上进行了相关实验，结果达到了技术要求。

FZXB