数码纱的外观效果仿真方法
喻 飞, 王静安, 潘如如, 周 建, 高卫东
(生态纺织教育部重点实验室(江南大学), 江苏 无锡 214000)
数码纺纱是一种能对所纺制纱线的纤维比例及纱线细度进行在线变化控制的纺纱方法,以多根粗纱异速喂入多个通道为本质特征,构建了以纱线长度为自变量、以纤维组分比例和纱线线密度为因变量的纱线特征函数,这种变化的纱线品种称为数码纱[1]。三通道数码纺纱是在环锭细纱机上以3个通道异速喂入粗纱,根据其喂入比例的变化规律将其分为混色纱、变色纱和段彩纱。数码纱相较于传统的纱线而言,具有颜色变化工艺复杂多样,颜色循环周期长的特征(通常长度可达几十米),因此用于描述数码纱的颜色变化规律,展示数码纱长周期外观效果的纱线模拟计算机辅助设计(CAD)系统对数码纱的工艺设计尤为重要[2]。
通过数码纱线的模拟,可对纱线的形态、颜色配比、循环周期等进行随意搭配设计,并且设计者可直观看到所设计的纱线效果,对数码纱工艺设计结果进行更加直观地反馈,对数码纱线的工艺设计具有重要的参考意义。针对传统各类纱线的仿真模拟已经有很多学者提出相关的理论。邓中明等[3]以图形化的方式对纱线参数化模拟,其核心思想是使用1组循环排列的倾斜的矩形色块来表示纱线的外观。马云芳等[4]在实际软件开发中对原有方法进行了改进,采用擦去4个角的平行四边形的方法来模拟,使纱线模拟的效果更加真实,并且程序实现也更加方便。诸葛振荣等[5-7]将纱线特征参数化为形态、材质和颜色3个主要方面,形态轮廓使用低次贝塞尔曲线来拼接构造,并在此基础上添加基于光照模型的颜色模型和随机噪声函数来表现纱线的材质。上述理论从初步实现花式纱线色纱模块的排列模拟到将光照、材质等参数引入纱线的模拟中,针对传统纱线的模拟理论逐步完善。由于传统的纱线在纺制过程中喂入比和纱线轴线方向变化相对稳定,所以现有的纱线模拟理论都是针对纱线短周期的特征模拟,而数码纱的特征为颜色变化多样,颜色循环复杂,且具有可长达几十米的颜色循环周期,因此,传统的纱线模拟方法无法反映数码纱长周期下的颜色变化特征,并不适应数码纱CAD的需求。
本文针对数码纱颜色循环复杂的特征,提出了用于数码纱长周期颜色特征表征的数字黑板模拟,实现通过输入的工艺参数,准确地将其映射到二维像素矩阵中,反映其颜色变化特征,同时采用合适的光照模型、颜色渐变模型以及颜色模块伪随机数模型等数学模型以获得更加真实的纱线外观,实现数码纱线的黑板模拟。最后通过与实际数码纱的黑板样图进行对照,验证了该方法的可行性。
1 数码纱的模拟
在线密度恒定的情况下,各组分根据色纱喂入比例不同可将数码纱分为3类:变色纱、混色纱、段彩纱。变色纱是指环锭细纱机纺制过程中,混色比不恒定,其中1根粗纱喂入量以逐渐减少(或增加)的形式变化,其余粗纱喂入量做出相应的变化以保持总喂入量不变,这样纺制出的纱线在黑板上呈现渐变效应。混色纱在纺制过程中各组分喂入比恒定,段彩纱在仿制过程中各组分纱依次喂入从而使纱线呈现分段色彩效应。混色纱和段彩纱可看作变色纱的2种特殊情况,所以该模拟算法主要以变色纱为例,以实现对数码纱长周期下的外观特征的模拟。
1.1 颜色的获取
各组分色纱的颜色是数码纱最重要的信息之一,是决定模拟结果是否接近真实数码纱外观特征的关键。本文采用实验室数码测色系统Digieye System 280获取颜色信息,将变色纱各组分对应的粗纱均匀绕在标准黑色样板上,并放入光箱,测得各组分色纱颜色的RGB值。图1示出粗纱黑板样本。

图1 粗纱黑板样本Fig.1 Roving blackboard samples
1.2 工艺参数的映射
数码纱相对于传统的纱线,最大的特点是其颜色配比工艺和颜色循环周期复杂多变。以变色纱为例,最常见的变色纱工艺为3种颜色粗纱喂入比分别两两递增(递减),以A、B、C表示3种粗纱的颜色,则1个周期内颜色的变化为A过渡到B再过渡到C,A与B及B与C的过渡过程喂入比变化梯度为10%,其中每段喂入比持续喂入时间为3 s。
根据工艺参数的规律,可将1个周期内的整段变色纱分成若干个固定喂入比的色纱段,将该喂入比下形成的纱段作为模拟的基本单元。设选取颜色A和颜色B喂入比为m∶k的纱段,其中m、k的和为100,则该色块单元映射到二维平面,形成W行、N列的像素矩阵E。
E=EΑEΒ
(1)
(2)
(3)
式中:EA与EB为颜色A、B对应的像素点矩阵;CA与CB为矩阵中每个像素点的值;i,j为矩阵中的第i行和第j列。
根据变色纱实际外观特征,每段色块颜色的交替不是呈梯度变化,而是在一定区间内缓慢过渡,在肉眼呈现颜色的渐变效果,在此将该区间称为渐变区间。计算机在模拟数码纱的过程中,数码纱线以矩阵的形式储存,最小的单元为1个像素点。数码纱颜色的渐变可通过对渐变区域各个像素点进行变换,建立各个像素点颜色分布与其所在列的位置的函数关系,从而实现颜色的缓慢过渡。设渐变区间为W行、L列的矩形矩阵,颜色变化由颜色A变化到颜色B。在A与B的渐变矩阵区间内,令每个第i行,第j列像素点的颜色选取符合参数为p的0-1分布的概率模型,p的取值根据对应像素点与颜色A、B的距离递增(递减)变化。若C(i,j)为渐变区域第i行,第j列像素点选取的颜色值,则:
(4)
Px=k=pk(1-p)1-k
(5)
式中:k=0,1且p=1-j/L;向量nA,nB为颜色A、B对应的RGB值。
引入渐变模型后,实际每段色纱纱段映射到二维平面的矩阵都可以由前段渐变区间H1、纯色区间C1、中间渐变区间H2、纯色区间C2以及尾部渐变区间H3所构成,如图2所示。其中纯色区间C1、C2中各像素点的值分别为nA、nB,根据上述所提出的渐变模型,H1中第j列各像素点的值为nA的概率p=0.5+j/L,H2中第j列各像素点的值为nB的概率p=1-j/L,H3中第j列各像素点的值为nA的概率p=j/L,由此得到各区间每个像素点的RGB值。

图2 色纱段基本单元颜色分布模型Fig.2 Color distribution model of basic unit of yarn segment
通过以上映射过程,可将变色纱各喂入比下形成的纱段单元在二维平面映射出来,然后根据每段的工艺排列顺序进行拼接,即可初步形成1个周期内的整段变色纱,模拟结果如图3(a)所示。

图3 色纱片段模拟结果图Fig.3 Fragment of yarn simulation results.(a) Mapping of color collocation and change; (b) Twist model; (c) Color module pseudo-random number model; (d) Illumination model
捻度对模拟的外观结果有直接的影响[8],捻度到模拟结果的映射可通过其捻回角来建立。捻回角为纱线加捻后表层纤维与纱条轴线所成的夹角,映射到模拟的色块则可近似用色块的倾斜角来表示。已知纱线的捻度和细度,根据式(6)可得到捻回角的正切值tanβ,最后根据捻向对模拟出的矩形色块进行倾斜变换,模拟的结果如图3(b)所示。
(6)
式中:β为捻回角;Tt为色纱的捻度,捻回数/10 cm;Nt为纱线的线密度,tex。
1.3 颜色模块伪随机数模型的建立
在数码纱实际生产过程中,罗拉根据设定的混纺比改变喂入速度,纺出按设定色纱混纺比的细纱,但是这个过程中罗拉转速变化的控制并不精确,导致实际纺制出来的细纱混纺比不是精确地按照设定混纺比变化。为更加真实模拟数码纱的循环变化规律,本文提出在准确按工艺设定混纺比的基础上,引入色块长度伪随机数Δ(采用线性同余算法[9]产生)。实际模拟的每段色纱各颜色色块的实际长度为
Lr=L+Δ
(7)
式中:L为根据色纱喂入比映射的理论色块的长度;Δ为伪随机数发生器产生的伪随机数。
通过建立色块长度伪随机数模型,实际模拟结果避免过于规律性,更加贴近实际变色纱的纺制结果,如图3(c)所示。
1.4 光照模型的建立
研究表明,物体表面的颜色不仅与光源有关,还受到环境光的影响,即物体表面的颜色包括对光源的镜面反射,环境光的漫反射[10]。距离越远,物体表面反射的光强越弱[11]。综合考虑,物体表面光强强度可表示为
(8)
式中:ka为物体的表面反射系数,ka∈[0 1];Ia为入射的泛光强度;d为光源到入射点的距离;k为常数。
对于单根细纱的光照强度,理论上纱线是圆柱体,但是考虑到纱线受自身重力的影响在平面上会产生变形,因此,其截面并不是标准的圆形。有研究者[12]将纱线看成椭圆柱状,纱线截面为椭圆形,则任意一点M(xi,yi)到模拟平面对应的亮度值为
(9)
式中:L0为椭圆界面垂直顶点亮度最大值;Y为纱线截面的宽度。
该模型克服了圆柱体模型的亮度渐变过快,边界暗处范围过大的弊端,模拟效果亮度渐变自然柔和;但是椭圆模型在实际模拟数码色纱时,亮度渐变过程中,亮度区间范围过大,变化不明显,暗处变化区间范围过小,于是本文针对此问题对椭圆光照模型做出调整。根据实际测量,光照变化在色纱表面光照强度最大点附近亮度平稳,变化幅度不大并向两侧缓慢衰减,这段区域基本与椭圆模型中光照变化规律相一致,但是变化到某点后,光强减弱幅度增大,于是色纱表面M点的光照强度可表示为
(10)
(11)
式中:L1为纱线表面x1点处的光照强度;La为纱线边界的光照强度。
在测得待模拟数码纱的颜色RGB值后,将其转化为LAB颜色空间,提取其L分量,并通过该光照模型计算新的各个像素点的L分量重新转换到RGB颜色空间,便可实现正常的光照效果,提升模拟仿真的效果,模拟纱线引入光照模型效果如图3(d)所示。
为完整显示整段变色纱的效果,建立数字黑板,将模拟出的变色纱分段映射到数字黑板,最终变色纱的整段周期在数字黑板的结果如图4所示。

图4 变色纱长周期数字黑板Fig.4 Digital blackboard of long fragment yarn
2 结果与讨论
为验证模拟结果的准确性,保证模拟的数字黑板外观效果与真实变色纱的一致性,采用JWF1551环锭细纱机试纺变色纱,变色纱工艺参数设定:线密度为47.6 tex,捻系数为380,捻度为697捻/m;3种色纱A、B、C颜色RGB值分别为(154,68,120)、(232,184,93)、(101,146,186);颜色循环规律为由A变化到B再变化到C,A—B及B—C的过程色纱喂入比以10%的梯度变化,每段喂入比下的持续时间为3 s。最后将试纺的变色纱绕在标准黑色背景的小黑板上,与模拟结果进行对比,如图5所示。通过对比可发现,通过该方法进行模拟的结果与真实变色纱的颜色基本一致,颜色循环变化规律也基本保持一致,可较好地呈现变色纱的颜色渐变效果,基本实现了对该变色纱的外观效果仿真。

图5 真实变色纱与模拟结果对比Fig.5 Comparison between real yarn (a) and simulated yarn (b)
数码纱较传统纱线最大的特点是颜色配色丰富多样,颜色循环变化复杂,在实际设计数码纱的过程中,配色方案以及粗纱喂入比梯度变化速率的改变对数码纱的外观效果有很大的影响。为保证该模拟方法可在数码纱线的颜色搭配、循环周期等进行随意设计的情况下仍然适用,对不同配色方案及不同粗纱喂入比梯度变化速率所纺的纱线进行模拟,并与实际纱线进行比较。
为验证在配色方案改变时模拟结果的稳定性,保持喂入比梯度变化速率(颜色A—B及B—C的喂入比以20%的梯度变化,喂入时间为4 s)不变,采用另一种绿、黄、蓝数码纱的配色方案,其中:绿色粗纱的RGB值为(40,128,131);黄色粗纱的RGB值为(232,185,93);蓝色粗纱的RGB值为(189,52,118)。纺制的真实纱线与模拟的数字黑板对照结果如图6所示。可看出,配色方案变化的条件下,该模拟方法也能较好地与原始纱线的整体外观效果保持一致。

图6 绿、黄、蓝搭配变化后模拟效果对比Fig.6 Simulation results of green-yellow-blue colors match comparison.(a)Real yarn; (b) Simulated result
为验证喂入比梯度变化速率改变时模拟结果的稳定性,采用相同的颜色搭配方案(即RGB值分别为(40,128,131)、(232,185,93)、(189,52,118)的红、黄、蓝3种颜色的粗纱,颜色变化工艺分别采用A—B—C的颜色变化过程中粗纱两两喂入的喂入比以30%和20%梯度变化,喂入时间为4 s。将纺制出的真实纱线与模拟结果进行对比,如图7所示。可看出,随着喂入比增减的梯度发生变化后,模拟出的变色纱周期发生变化,颜色替换的快慢也随之改变,并能够与真实的纱线颜色的变化基本保持一致,可基本反映真实纱线的外观效果。
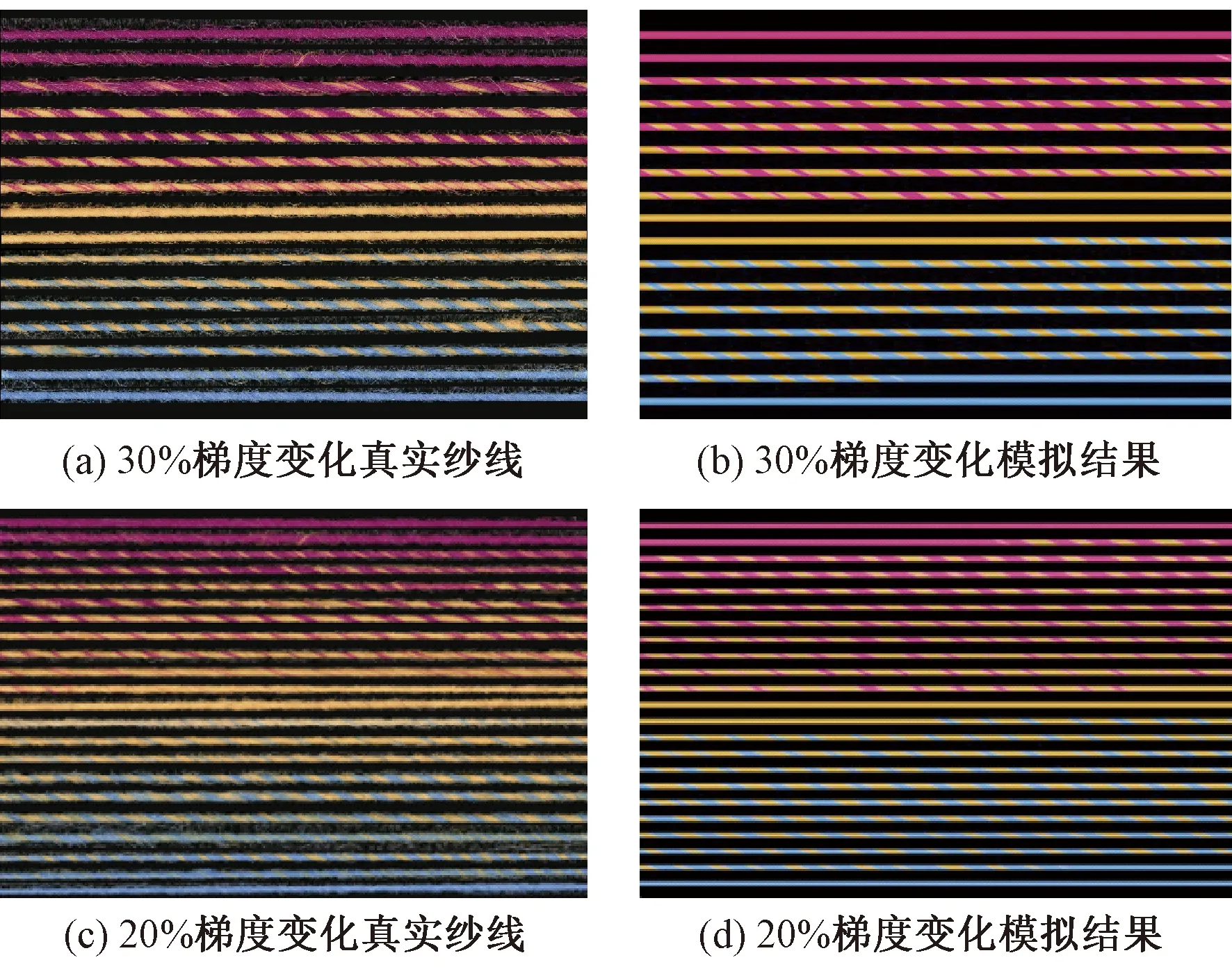
图7 不同喂入比增减梯度下模拟效果对比Fig.7 Comparison of simulation results under different feed ratio gradients.(a) 30% gradient change of real yarn; (b) 30% gradient change of simulated result; (c) 20% gradient change of real yarn; (d) 20% gradient change of simulated result
3 结束语
针对数码纱颜色变化工艺复杂多样,颜色循环周期长的特征,采用数字黑板模拟数码纱,以反映长周期下数码纱的颜色变化规律和外观效果,并建立了相应的光照模型、颜色渐变模型和颜色模块伪随机数模型。选取多种典型变色纱的工艺参数进行映射,其结果可准确映射数码纱对应的工艺参数,真实反映相应工艺参数下数码纱颜色的变化规律和外观效果。
数码纱的数字黑板模拟可为设计数码工艺的过程提供参考与反馈,是数码纱CAD重要的组成部分。在今后的研究中,将会把数码纱的毛羽及条干变化因素考虑到数码纱模拟的过程中,以得到更加真实的外观效果。
FZXB

