多工序递阶的棉纺过程质量智能控制模型

邵景峰， 马创涛

(西安工程大学 管理学院， 陕西 西安 710048)

在中国制造2025战略下，随着我国棉纺企业数字化车间建设进程不断推进和传感器的大量应用，整个棉纺生产过程积累了大量的与质量相关的数据，而这些数据之间因存在自相关性，从而导致纺纱质量难以精准控制。

国外研究者对该问题的研究主要集中在基于质量预测的反馈控制方面。如：FATTAHI S等[1]利用稳健回归和附加平方和提出了一种纺纱质量预测方法，并通过输入纤维属性来预测纺纱质量的拉伸、不匀和毛羽等性能指标；NURWAHA D等[2]研究了一种基于多层感知神经网络、支持向量机(SVM)以及径向基函数神经网络的纱线质量智能控制系统，该系统通过模型对纱线的质量属性等知识进行学习，从而实现纱线质量的控制，但不足之处在于其纱线控制精度较低;与此同时，SELVANAYAKI M等[3]提出了一种基于支持向量机的纱线强力波动行为预测与控制方法。随着理论研究的不断深入，研究聚焦于基于智能优化模型与专家系统相融合的纺纱质量智能控制方面。如MOZAFARY V等[4]提出了一种将聚类和人工神经网络相结合的数据挖掘算法，并将其用于纺纱质量控制；ENGIN A B[5]通过实验验证了一种基于自动控制系统的材料均匀度控制方法，该方法减少了因原料问题而导致的纱线质量波动；ELASHMAWY I等[6]研究了基于模糊集的纺纱质量控制方法，可更加精确地控制纺纱质量。

国内研究者也探讨了纺纱质量的控制问题，研究的焦点集中于单一工序的质量控制：吕志军等[7]提出了基于SVM的纱线质量预测模型，解决了纱线质量控制过程中过多依赖领域专家和管理者经验的问题，实现了对纱线质量的反馈与控制；张圣忠等[8]以梳棉机系列工艺试验优化为例，探讨了正交试验、统计分析在纺纱质量控制中的具体应用；孙林[9]提出了一种基于加权最小二乘支持向量机(WLS-SVM)时间序列的产品质量控制方法。随着纺织过程智能化水平的不断提高，研究者着手研究多工序的纺纱质量预测与控制问题：李荟萃等[10]构建了面向纺织生产全生命周期的质量数据模型及质量控制系统，实现了对纺纱产品质量的预测与控制；杨建国等[11]建立了基于改进极限学习机(ELM)算法的预测模型，并将其用于毛纱条干CV值的预测，相对误差可降低2.70%；KUO C F J等[12]采用模糊神经网络对纺纱生产过程中多工序间的卷取辊速度等工艺参数进行学习和训练，通过不断调整网络隶属函数的平均值和标准偏差以及网络间的连接加权值，从而控制纱线均匀度。

综上，国内外学者们对纺纱质量控制的研究主要是基于2～3个纱线质量指标及其相关关系而构建的单一工序的纺纱质量控制模型；尽管近些年来有研究者从多工序的视角对纺纱质量进行了探讨，但大多数研究集中在纺纱质量的预测上，而有关多工序纺纱质量控制的文献报道甚少，尚未实现基于多工序递阶的棉纺过程质量控制。目前以下2个问题亟待解决：1)如何实现纺纱过程多工序间知识关联的纺纱质量控制；2)如何发挥大量小数据在纺纱质量控制中的优势。为此，本文在对棉纺质量波动行为进行分析的基础上，选取断裂强度为质量控制指标，并基于多工序质量控制点间的递阶关系模型，构建多工序递阶的纺纱质量控制模型，并借助棉纺过程产生的大量小数据及多目标烟花算法，实现纱线质量的多工序控制。

1 质量指标选择及影响因素分析

1.1 纱线质量波动关键指标的辨识

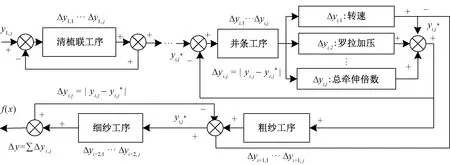
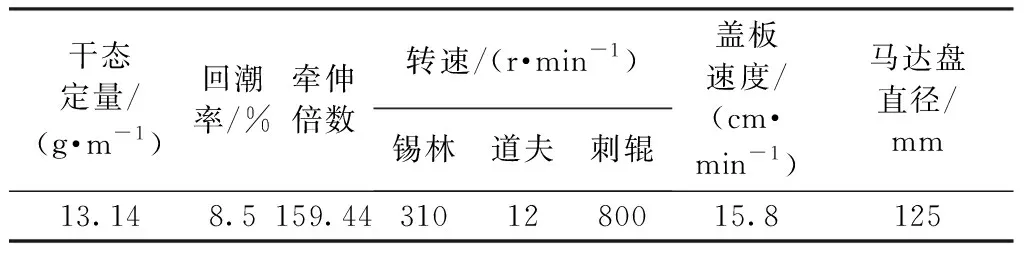
根据纱线质量国家标准，用来表征纱线质量的主要指标可分为质量偏差、质量变异系数、单纱断裂强度、棉结杂质粒数、捻系数、条干均匀度、粗节、细节、断裂伸长率等。为选取影响纱线质量波动的关键指标进行控制，首先基于纺织企业纺纱车间生产统计管理系统中的纱线质量管理子系统，构建棉纺大量小数据存储系统。然后，选取纱线细度不匀、粗节、细节、断裂强度和断裂伸长率5个纱线质量指标为主要质量指标。从构建的数据存储系统中选取如表1所示的与纱线细度不匀、粗节、细节、断裂强度和断裂伸长率相关的25个试样数据。其中误差数据表示纺纱生产过程中不同纱线质量指标波动的大小，断裂伸长率表示纺纱生产过程中断裂伸长的波动。为此，对上述5个影响纱线质量波动的关键指标进行分析，图1示出纺纱过程质量波动的统计结果。

表1 纱线质量波动试样数据表Tab.1 Sample data of yarn quality fluctuation

图1 纺纱过程质量波动过程统计结果Fig.1 Statistical results of quality fluctuation process in cotton spinning process based on data analysis

由图1可知，在细度不匀、粗节、细节以及断裂强度和断裂伸长率这5个关键质量指标中，断裂伸长率、断裂强度以及细度不匀受异常因素影响较大，其中断裂强度受异常因素影响波动最为显著。同时，断裂强度与纤维的种类、粗细、捻度、细度不匀率之间呈一种正相关关系，而且由于纱线在整个纺纱过程中受众多复杂机械力的作用，易被拉伸、弯曲和扭转，因此断裂强度是影响纱线质量的关键指标。为此，选取纱线断裂强度为主要控制指标，并在分析影响纱线断裂强度关键因素的基础上，构建基于多工序递阶的棉纺过程质量智能控制模型。

1.2 影响纱线强度关键因素分析

按照纺纱工艺理论，纱线强度主要由纤维性能和纱线结构决定[13]。抛开纤维种类影响因素，纤维性能和纱线结构很大程度上取决于纺纱生产过程中各个工序的工艺。现以棉精梳纱生产过程为例对各个工序中影响纱线强度的关键因素进行分析。

在精梳纱生产过程中，清棉工序中纤维的长度、整齐度以及断裂强度越高，其对应的成纱强度越高[14]。梳理工序中刺辊和锡林转速是影响梳理效果的主要因素之一[15]，随着锡林转速和刺辊转速的提高，可减少棉结和杂质，进而提高纤维的整齐度与断裂长度[16]；同时，减小精梳工序中梳理隔距可降低因纤维相互揉搓而产生的棉结，并提高纱线质量[17]。并条工序中罗拉转速可通过影响并条工序中棉纤维混合的均匀度最终影响纱线强度[18]；同时适当控制回潮率可使生条中各种不同形状的纤维充分混合，进而提高纤维分子间的抱合力及成纱强度[19]。粗纱工序中粗纱回潮率可通过影响纱线牵伸后纤维的应力并最终影响纱线强度[20]；同时粗纱捻系数会通过影响粗纱纤维间的抱合力进而影响纱线强力[21]。在细纱工序中，适当控制细纱工序中的牵伸倍数和细纱机的锭速，可提高纱线断裂强度[22-23]。

为此，从纺纱流程出发，对影响纱线断裂强度的关键因素总结如下：在清棉工序中，影响纱线断裂强度的主要因素有纤维长度、纤维整齐度以及纤维断裂长度；在梳棉工序中，影响纱线断裂强度的主要因素有刺辊转速、锡林转速；在精梳工序中，影响纱线断裂强度的主要因素有梳理隔距、罗拉转速；在并条工序中，影响纱线断裂强度的主要因素有回潮率、罗拉转速；在粗纱工序中，影响纱线断裂强度的主要因素有回潮率、捻系数；在细纱工序中，影响纱线断裂强度的主要因素有牵伸倍数、锭速等。

2 棉纺过程质量控制模型

2.1 质量控制点及质量损失函数设计

在纱线质量指标选择及对影响其波动关键因素进行分析的基础上，构建了如图2所示的面向纺纱过程多工序递阶纱线断裂强度控制点框图。

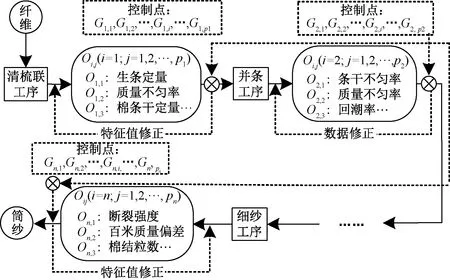
图2 多工序递阶的纱线断裂强度控制点框图Fig.2 Diagram for yarn fracture control points based on multi-process hierarchy

这样，每个工序Si都有对应的质量控制点Gi,j以及对应质量控制点的质量输出特征值Oi,j。此外对于纺纱质量控制点集合G中的任一个质量控制点Gi,j，都有与其对应的工艺参数的实际值yi,j及其控制阈[L1(Gi,j),L2(Gi,j)]，即工序集合S、质量控制点集合G以及工艺参数集合间存在相互映射关系。基于此，利用人机系统工程学理论，从人、机、系统、料、工艺等角度着手，在文献[24]中提出的改进的质量损失控制阈函数的基础上，定义面向纺纱过程中各工序间表达纱线断裂强度的多载荷影响因子：

(1)

在式(1)定义的多载荷影响因子的基础之上，结合纺纱生产的具体工艺流程，定义如式(2)所示的第i个工序、第j个质量控制点的质量损失函数：

(2)

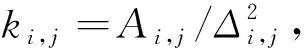
进而，在式(2)定义的每个工序质量控制点质量损失函数的基础上，对于纺纱过程中具体工序而言，有如式(3)所示的质量损失函数：

(3)

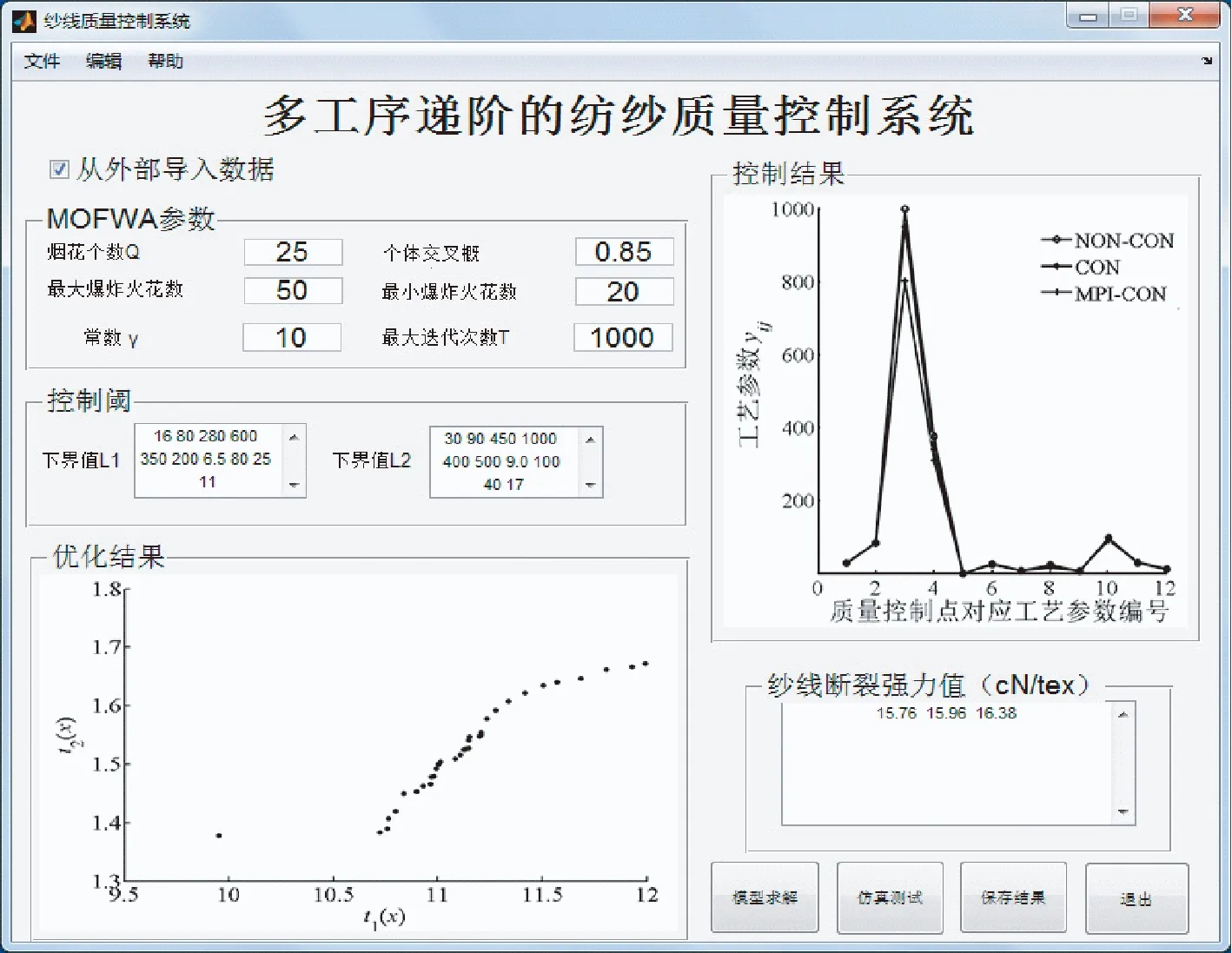
式中：Ci(yi,j)表示第i个工序、第j个质量控制点的质量损失函数；fi(x)表示第i个纺纱工序的质量损失函数；0

2.2 质量控制模型构建

2.2.1模型构建

对于整个纺纱系统而言，上游工序的质量输出对下游工序质量输出以及最终纱线的质量输出都会产生影响。当然，从根本上讲，这种影响主要源于分布在不同工序质量控制点之间存在着相互作用关系，具体表现为从清梳联、精梳、并条、粗纱以及细纱等生产工序中上游质量控制点到下游质量控制点依次向下传递和累加的过程。为表达纺纱系统中多工序质量控制点间的相互作用关系，基于文献[25]提出的多阶段质量预测模型，按照棉纺工艺流程中的各质量控制点间输入—输出关系，建立基于多工序递阶的纺纱质量输出特征值知识关联模型。

对于式(3)中定义的各工序质量控制点对应的质量损失函数f(x)={f1(x),f2(x),…,fi(x),…,fn(x)}，某一具体工序质量损失函数可表示为式(4)所示的单个工序内各个质量控制点质量损失函数的串联关系：

∏[f1(x),f2(x),…,fi(x),…,fn(x)]

(4)

对于整个纺纱过程而言，纱线质量可视为一种以制品为载体的质量损失的传递和累加过程，因而纺纱质量控制问题可视为一种优化问题，通过不断地迭代和寻优求解得出质量损失最小时对应的各个质量控制点工艺参数的最优解。为此，在上述定义的纺纱质量控制点及其耦合作用关系的基础上，建立纺纱质量优化目标函数：

(5)

进而，基于式(1)～(4)展开式(5)的纺纱质量优化模型目标函数，可得到如式(6)所示的纺纱质量优化模型：

(6)

s.t.

式中：βi,j为考虑影响纱线断裂强度的原料因素、工艺因素以及设备因素等多种因素间相互作用下的多载荷影响因子；Oi,j为纺纱生产过程中第i个工序中的第j个质量控制点的质量特征输出值；Cmpt为工序能力指数。

2.2.2基于数据的反馈机制

2.5 两组患者术后并发症发生率比较 两组患者术中均未见盆腔器官损伤发生。两组患者术后并发症发生率比较差异无统计学意义(χ2=0.519，P>0.05)。见表6。

在得到各个质量控制点优化后的工艺参数值的基础上，采用自动过程控制(APC)技术[26]对纺纱生产过程进行反馈调整，构建如图3所示的基于数据反馈的棉纺过程质量控制模型。

图3 基于数据反馈的棉纺过程质量控制框图Fig.3 Diagram for quality control based on data feedback

2.3 基于多目标烟花算法的控制模型求解

2.3.1约束条件的处理

对于非线性优化问题的求解，随着实际工程应用中目标函数的不连续且不可微，使得传统的求解优化问题的方法具有很大的局限。由于进化算法只要求目标函数值是可计算而不要求其具有连续可微的性质，因而其在处理复杂优化问题方面表现出了较优的性能。当然，进化算法作为一种无约束的进化搜索技术，在求解约束优化问题前需要对其约束条件进行处理[27]。为此，在式(6)求解过程中，需要构建一个惩罚函数，将单目标多约束优化问题转换为双目标优化问题，并实现对约束条件进行处理，具体步骤如下。

第1步，引入惩罚函数H(x)对模型中的约束条件进行处理：对于前q个等式约束条件gi(x)，需要通过引入等式约束违反的容忍值δ转换成为不等式约束，对于其他的r-q+1个不等式约束条件hi(x)不做处理。

(7)

第2步，定义式(8)所示的双目标函数：

(8)

式中：t1(x)为原模型中的目标函数，且t1(x)=f(x)；t2(x)为违反约束条件的最大惩罚度，且t2(x)=H(x)。当且仅当t2(x)≥0时，变量x满足所有约束条件。同时，当t1(x)取得最小值时，可以搜索到纱线断裂强度损失值最小时的最优工艺参数可行解集合。当t1(x)和t2(x)同时取得最小值时，不但可搜索到最优工艺参数集合的可行解，而且可确保各个质量控制点的工艺参数在对应控制阈范围内，即可搜索到纱线断裂强度损失值最小时的最优工艺参数解集合。

第3步，通过上述转换策略将原单目标优化模型转化为如下式所示的双目标优化模型：

2.3.2模型求解算法

多目标进化算法在每次执行过程中可确定多个帕累托最优解[28]，被认为是求解多目标优化问题最有效的方式，为此，基于多目标烟花算法(MOFWA)在解决多目标优化问题时表现出的寻优性特性[29]，经过多次仿真实验和结果的对比分析，采用MOFWA算法对基于多工序递阶的棉纺过程质量控制模型进行求解及控制，具体求解流程如图4所示。

图4 多工序递阶的棉纺过程质量控制流程图Fig.4 Flow diagram of quality control for cotton spinning based on multi-process hierarchy

基于图4中的流程图，对具体的流程进行梳理，并从以下5个步骤进行具体阐释。

在此基础上，利用质量控制点Gi,j对应的控制阈函数中的实际工艺参数yi,j来初始化烟花算法。

第2步，选择适应度函数。选取棉纺过程质量优化模型中的目标函数，将其作为多目标烟花算法的适应度函数，通过算法不断地进化和迭代以及适应度函数的评估，获得整个棉纺过程质量优化模型的最优解。具体适应度函数如式(11)所示。

(11)

第3步，烟花种群寻优。对于式(11)中任意解yi,j，计算初始烟花个数N、爆炸火花数m、最小烟花爆炸火花数Smin、最大烟花爆炸火花数Smax。进而，对于解空间中每个解，随机选择其他2个解，通过式(12)所示的变异策略进行差加权操作并得到变异解，同时利用式(13)的交叉策略对原解和变异解xi进行交叉操作，从而得到交叉解ui，即：

Vi=xc1+γ(xc2-xc3),c1,c2,c3∈{1,2,…,m}

(12)

(13)

式中：γ为常数且γ>0；θ为烟花个体交叉概率且θ∈[0,1]；ci为区间(0,N]内的随机整数。

第4步，选择最优解。在式(12)、(13)的基础上，构建如式(14)所示的选择策略。如果生成的交叉解ui的适应度值r(ui)>r(xi)，则用ui替换xi，并利用ui更新解空间，即从当前种群中选择适应度值较好的个体组成新的烟花种群，并通过烟花种群的不断迭代获得最优解：

(14)

第5步，获得最优解并进行反馈更新。如果满足终止条件，则求解过程停止并获得最优解及其工艺参数容差，若容差超出对应的质量控制阈，则利用最优解对工艺参数进行更新，实现对纱线质量的反馈控制。否则，返回执行第3步。

3 算例验证与结果分析

3.1 数据选取

以咸阳某纺织厂为例，其主要纺纱工序为开清棉、梳棉、精梳、并条、粗纱、细纱及后加工等工序，因而将棉纺过程质量控制关键工序集合定义为S={S1,S2,S3,S4,S5,S6}。其中：S1表示清棉工序；S2表示梳棉工序；S3表示精梳工序；S4表示并条工序；S5表示粗纱工序；S6表示细纱工序。

为此，选取如表2～7所示的该企业纺纱车间精梳7.29 tex(JC7.29 tex)品种纱线的工艺数据作为实验数据集。进而，采用多目标烟花算法对2.2节中建立的基于多控制点的棉纺过程质量优化控制模型进行求解，并进行具体的应用验证分析。

表2 清棉工序JC7.29 tex工艺数据Tab.2 Process data of JC7.29 tex in cleaning process

表3 梳棉工序JC7.29 tex工艺数据Tab.3 Process data of JC7.29 tex in carding process

表4 精梳工序JC7.29 tex工艺数据Tab.4 Process data of JC7.29 tex in combing process

表5 并条工序JC7.29 tex工艺数据Tab.5 Process data of JC7.29 tex in drawing process

表6 粗纱工序JC7.29 tex工艺数据Tab.6 Process data of JC7.29 tex in roving process

表7 细纱工序JC7.29 tex工艺数据Tab.7 Process data of JC7.29 tex in spinning process

进而，在如图2所示的多工序递阶的纱线断裂强度控制点框图的基础上，结合该纺织企业历史工艺数据，建立如表8所示的多工序递阶的纱线断裂强度的质量控制点及其控制阈。

表8 纱线断裂强度的质量控制点及其控制阈Tab.8 Quality control points and control threshold of yarn breaking strength

3.2 参数设置

3.2.1模型参数设置

对于模型参数的设置，主要包括工序能力指数Cmpt、多载荷影响因子βi,j以及质量损失函数中的系数k，具体计算如下。

1)工序能力指数。根据GB/T 398—2008《棉本色纱线》中的纱线质量标准以及该纺织企业纱线产品质量控制要求，得到JC7.29 tex品种的优等纱线产品单纱断裂强度的质量规格为(16.40±0.02)cN/tex，取σ=0.025，则工序能力指数为

2)多载荷影响因子。根据该纺织企业历史工艺设计数据显示，对于JC7.29 tex品种纱线，当细纱工序中的锭速和牵伸倍数分别为12.72 kr/min、28.12时生产纱线断裂强度最高；同时从细纱机读取的实际锭速数据为13.765 kr/min。为此，在表8中建立的多工序质量控制点及控制阈的基础上，结合该纺织企业JC7.29 tex纱线的历史工艺数据，以细纱工序中的锭速控制点为例，并选取该质量控制点常数B=0.24,进而计算多载荷影响因子：

3.2.2多目标烟花算法参数设置

根据求解的具体问题以及在文献[30]研究的基础上，对多目标烟花算法的参数设置为：烟花个数N=25，最大爆炸火花数Smax=50，最小爆炸火花数Smin=20，常数γ=10，烟花个体交叉概率θ=0.85，算法最大迭代次数T=1 000。

3.3 算例分析与验证

在计算得到的工序能力指数Cmpt和多载荷影响因子βi,j以及系数ki,j的基础之上，以该企业生产的JC7.29 tex品种纱线为例，对本文提出的多工序递阶的棉纺过程质量控制模型进行具体验证。

现以该纺织企业纺纱生产的细纱工序为例，结合纺纱生产过程中的历史工艺数据以及上述计算得出的参数值，说明纺纱各工序中的质量损失值的计算过程。

首先，将细纱工序中细纱机的锭速实际的锭速值13.765 kr/min和控制阈函数目标锭速值12.72 kr/min代入式(2)中，计算细纱工序中细纱机锭速对应的质量控制点的质量损失值：

表9 纱线断裂强度控制对比结果Tab.9 Comparison control results of breaking strength of yarn

类似地，分别计算细纱工序中其他质量控制点的质量损失值C6(y6,1)，并基于式(3)计算整个细纱工序的质量损失值：

进而，根据式(4)对整个棉纺生产过程的质量损失函数进行具体分析，得到结果如下：

f(x)=∏[f1(x),f2(x),…,f6(x)]

最后，将上述参数代入式(6)所定义的多工序递阶的棉纺过程质量优化模型，得到如下所示的棉纺过程质量控制模型的目标函数：

基于此，在MatLab R2014a的GUI集成开发环境下，开发了如图5所示的基于多工序递阶的棉纺过程质量控制模型可视化实验平台。

图5 棉纺过程质量控制模型可视化平台Fig.5 Platform of spinning quality control system

基于上述平台，选取该纺织企业纺纱车间5个批次JC7.29 tex品种纱线的质量及工艺数据，采用多目标烟花算法对上述建立的纺纱质量控制模型进行求解，经过20次迭代得到了如图6所示的pareto前沿。

图6 采用MOFWA得到的pareto前沿Fig.6 Pareto front based on MOFWA

由图6可知：在解集的分布方面，整个解集的分布相对集中，并且当目标函数t2(x)对应的惩罚度值较小时，对应的质量损失函数t1(x)值较小；随着目标函数t2(x)对应的惩罚度值越来越大，对应的质量损失函数t1(x)值也逐渐变大。

为验证多工序递阶的棉纺过程质量控制模型的有效性，分别对考虑多工序间耦合作用的棉纺过程质量控制模型MPI-CON(multi process influence-control)的控制结果与未考虑多工序间耦合的棉纺过程质量控制模型CON(control)控制结果以及控制前NON-CON(non-control)的结果进行对比，并统计控制前后因纱线断裂强度不符合标准而出现的不合格品率，得到了如表9所示的结果。

由表9可知，基于多工序递阶的棉纺过程质量控制模型控制结果与未考虑多工序间耦合作用的棉纺过程质量控制模型控制结果以及控制前的结果相比，纱线断裂强度值分别提升了1.27%和3.40%，同时因纱线断裂强度不符合标准而导致的纱线不合格品率分别降低了23.48%和50.00%。

同时，在表9所示控制对比结果的基础上，分析得到了如图7所示的不同控制模型各个质量控制点对应工艺参数优化控制结果对比图。

图7 优化控制前后工艺参数对比结果Fig.7 Comparison results before and after optimization control for technical parameters

由图7可知，在纱线断裂强度相同的条件下，采用基于考虑多工序间耦合作用关系的棉纺过程质量控制模型(MPI-CON)得到的控制结果与未考虑多工序间耦合作用关系的棉纺过程质量控制模型(CON)得到的控制结果以及控制前(NON-CON)的结果相比，在质量控制点3以及控制点4上对应的工艺参数要求有了降低。进而，也说明本文提出的质量控制模型可通过对各个质量控制点工艺参数的优化，提高纱线产品的断裂强度。

本算例结果表明，本文提出的基于多工序递阶的棉纺过程质量控制模型，不仅提高了纱线断裂强度，降低了纱线的不合格品率，而且也在保证纱线断裂强度不下降的条件下，降低了纺纱生产过程中的原料、设备以及工艺参数等要求，实现了纱线断裂强度的多工序控制。

4 结束语

本文从影响纱线质量异常波动的关键因素出发，对纱线断裂机制和影响纱线断裂强度波动的关键因素进行分析，并选取纱线断裂强度为主要控制指标，建立纺纱质量控制点耦合知识的关联表达方法及质量损失函数。进而，以质量损失函数为目标函数，构建基于多工序递阶的棉纺过程质量控制模型，并借助自动过程控制技术，实现了断裂强度的控制。最后，以咸阳某纺织企业生产的JC7.29 tex纱线品种为例，对该模型进行了具体应用分析。结果表明：该模型可通过对各个质量控制点工艺参数的优化，提高纱线断裂强度，降低因纱线断裂强度不达标而导致的纱线不合格品率，实现了纺纱质量的多工序控制，由于棉纺过程质量控制是一种实时在线的反馈控制，当上游工序中棉纺过程质量输出特征值波动时，需要及时地对下游工序中质量控制点的工艺参数进行在线反馈和调整，故研发棉纺过程质量在线控制系统将是下一步研究的重点。

FZXB