磁斯格明子器件及其应用进展∗
夏静 韩宗益 宋怡凡 江文婧 林柳蓉 张溪超 刘小晰 周艳
1)(香港中文大学(深圳)理工学院,深圳 518172)
2)(信州大学工学部电子信息系统工程系,日本 3808553)
磁斯格明子是一种具有准粒子特性的拓扑纳米磁畴壁结构.由于磁斯格明子具有较好的稳定性和新奇的动力学特性,并可被磁场、电场、电流等方式调控,有望成为高密度、低耗能、非易失性信息存储及逻辑运算的新兴信息载体.自2009年磁斯格明子首次被实验观测到至今,已有多种基于磁斯格明子的器件概念和原型器件被提出.本文对基于磁斯格明子应用的研究进展进行综述,对现阶段几种具有代表性的磁斯格明子器件应用进行简要介绍、分析和总结,包括基于磁斯格明子的赛道存储器件、逻辑计算器件、类晶体管功能器件和纳米级微波振荡器;同时阐述了几种可能的通过磁斯格明子表达二进制信息元的方法;并展望了磁斯格明子的其他潜在应用以及未来基于磁斯格明子器件应用的发展方向.
1 引 言
随着大数据分析和人工智能等高新科技逐步进入到人们的日常生活中,整个社会对信息存储的需求也与日俱增,亟需密度更高、读取速度更快的信息处理设备.由于磁斯格明子具有尺寸小、稳定性高、功耗低等特点,极有希望成为新一代信息元载体.
磁斯格明子可以稳定地存在于各种不同种类的材料中,包括磁性材料[1−8]、亚铁磁材料[9]、反铁磁材料[10,11]、多铁材料[12]、铁电材料[13]等.此外,磁斯格明子的稳定也存在几种不同的机制,包括由重金属与铁磁材料耦合诱导产生的Dzyaloshinskii-Moriya(DM)相互作用[6,7,14,15]、阻挫交换作用[16−21]、以及纳米图案成型[22].不仅如此,磁斯格明子可采用多种方式进行调控,如磁场[23,24]、自旋电流[7,8,25−28]、电场[29−32]、自旋波[33−35]、微波[36,37]、应力[38−41]、激光[42,43]、温度梯度[44]等.磁斯格明子的多样性和灵活性表明它具有巨大的潜在应用价值,尤其是在信息处理方面.
在信息处理过程中,通常可采用二进制编码.在基于磁斯格明子器件中,二进制“0”和“1”存在多种可能的表达方式,如图1所示.在图1(a)中,用斯格明子和铁磁态分别代表信息元“1”和“0”[26,45].也可以用中心磁矩朝上的斯格明子表示“0”,而中心磁矩朝下的斯格明子表示“1”,如图1(b)所示.图1(c)中的奈尔型和布洛赫型的磁斯格明子也可以表示“0”和“1”[19].在人工反铁磁耦合结构中,可以用两对中心磁矩方向不同的反铁磁耦合磁斯格明子分别表示“0”和“1”[46],如图1(d)所示.在三维体材料中,可以用磁斯格明子管(skyrmion tube)和浮子(bobber)来分别表示“0”和“1”[47],如图1(e)所示.
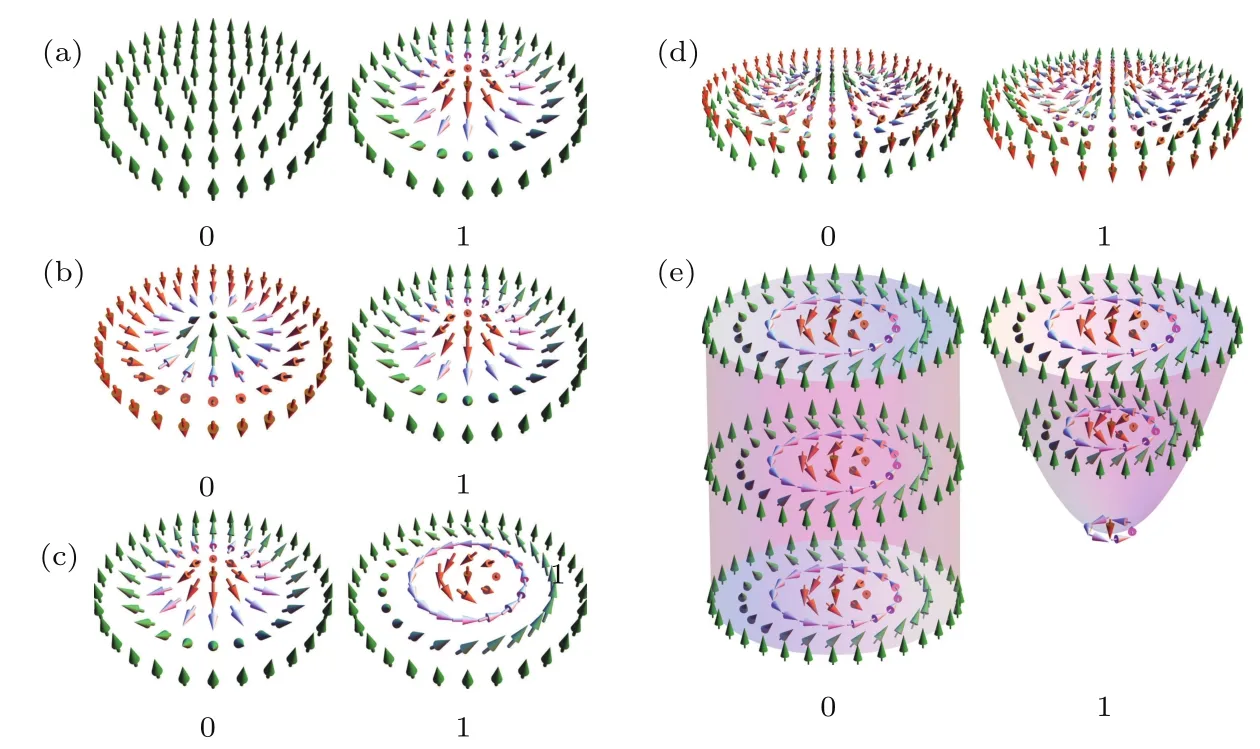
图1 基于磁斯格明子的信息元“0”和“1”的不同表达Fig.1.Possib le methods of encoding binary bits “0” and “1” in magnetic skyrmion-based devices.
2 基于磁斯格明子的赛道存储器
磁性存储器作为主要的数据存储媒介已经有半个多世纪的历史,它的发展使世界进入了大数据时代.赛道存储器(racetrack memory)[48]是一种正在开发中的非易失性信息存储器件,基于磁畴壁的赛道存储器将磁畴作为磁存储单元.与传统的磁存储器不同的是,在赛道存储器中,存储、写入和读取信息的设备是固定的,通过自旋极化电流的短脉冲使信息元沿着纳米导线移动,信息则由与赛道连接的读取设备读出.由于数据以磁畴的形式存储在赛道中,可以通过电流控制磁畴的运动,从而操纵赛道中存储的信息.由于磁斯格明子具有尺寸小和稳定性好等优势,基于磁斯格明子的赛道存储器[25,45,49−53]应运而生.
在基于磁斯格明子的赛道存储器中,二进制基本信息元(0或1)可通过磁斯格明子来编译.最简单的方法是由磁斯格明子的存在代表“1”,反之代表“0”.如图2所示,基于磁斯格明子的赛道存储器主要由四个部分组成,其中包括写入磁斯格明子的磁头,传输磁斯格明子的纳米赛道,读取信息的磁头和用来产生电流的CMOS(互补金属氧化物半导体)回路.通过从写入磁头注射自旋极化电流产生磁斯格明子,再由驱动电流驱动磁斯格明子沿着纳米赛道移动.最终,由读取磁头检测磁斯格明子.当需要消除无用的信息时,只需要注入驱动电流将磁斯格明子推出纳米赛道即可.
磁斯格明子在赛道存储应用方面有着显著的优势.首先,在功耗方面,基于磁斯格明子的赛道存储器功耗更低.传统磁畴壁的启动电流约为1—2.5×1011A/m2[54,55],磁斯格明子晶体的启动电流低至106A/m2[56,57]. 与磁畴相比,磁斯格明子的尺寸小,在几纳米到几十纳米之间[1−3,5,9,58,59].另外,由于与边界的排斥作用[45,53],斯格明子的运动不受轨道形状的影响,可以在弯曲或者有缺陷的轨道中运动.除此之外,斯格明子的拓扑稳定性减少了在一些不良条件下的信息的损耗和波动,这让基于斯格明子的赛道存储器的信息保存的鲁棒性更高.这一系列的优势让斯格明子在赛道存储方面的应用具有极大的潜力.
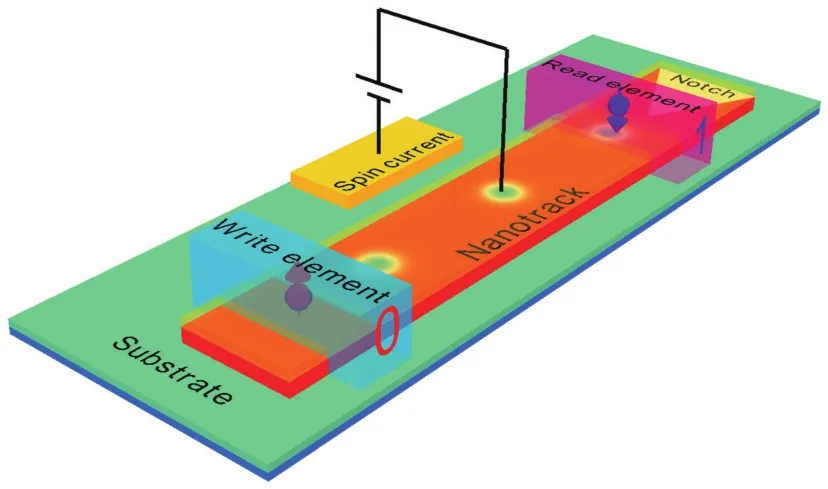
图2 基于磁斯格明子的赛道存储器示意图[53]Fig.2.Illustration of skyrmion-based racetrack memory[53].
在基于斯格明子的赛道存储器实际应用之前,还需要解决一些问题.在高密度数据存储的前提下,斯格明子之间的距离要求尽量小.在运输一段较长的信息时,由于斯格明子之前存在相互排斥的作用力[45,53],斯格明子会重新均匀分布,最终导致错误的信息输出.因此,斯格明子之间的距离要大于一定值才能保证信息传输的准确性[53],但是这就大大降低了信息存储的密度.为了解决这个问题,一种由电场控制的Y型轨道被提出[60].在该模型中,比特值(0或1)不再只由一条赛道中是否存在磁斯格明子决定,而是分别由两条赛道中存在的斯格明子来决定.虽然这个模型提高了信息的准确度,但是赛道数量的增加也降低了信息的存储密度.值得一提的是,也可使用已在基于畴壁的赛道存储相关研究中提出的方法,即通过在轨道上刻出均匀分布的凹槽来稳定斯格明子之间的距离[48].这个方案可以在不改变轨道数量的前提下有效地改善信息传输的准确度,但是轨道上的凹槽可能在一定程度上降低了斯格明子的移动速度.
另外,磁斯格明子在被自旋极化电流驱动时,由于马格努斯力(Magnus force)的作用,斯格明子会在横向方向发生位移,无法沿驱动电流的方向做直线运动,这个现象被称作磁斯格明子霍尔效应(SkHE)[8,9,46].为了消除斯格明子霍尔效应,人工合成反铁磁耦合的双层纳米轨道被提出[46].两个垂直磁化的铁磁层之前存在反铁磁耦合(AFM),当驱动电流从底部的铁磁体层注入时,铁磁层之间的强耦合作用使顶部和底部铁磁体层的斯格明子保持同步运动.与此同时,由于作用在顶层和底层斯格明子的马格努斯力的相互抵消,反铁磁耦合的两个斯格明子可以在轨道中间保持直线运动而不受马格努斯力的影响.这为基于斯格明子的存储器件和逻辑计算设备的实现铺下了坚实的基石.另一种解决方案就是单相反铁磁材料中的斯格明子[10,11].在单相反铁磁材料中,相邻的磁矩具有方向相反、大小相同的特性,因此,反铁磁材料中的斯格明子可以看成是两个方向相反的斯格明子套构在一起.当注入电流时,两个斯格明子受到的马格努斯力大小相同方向相反,相互抵消,因此,反铁磁斯格明子可以不受马格努斯力的影响而在轨道中间保持直线运动.
3 基于斯格明子的逻辑门
斯格明子不仅可以用于构建赛道存储器件,还可以用来做逻辑计算[61,62].研究表明,磁畴壁和斯格明子之间转换是可逆的[63],如图3所示.一系列的磁畴壁在较窄的纳米轨道上传输,随后在较宽的纳米轨道中成对的磁畴壁被转化为一连串的斯格明子,这些斯格明子最终再次被转化为磁畴壁.

图3 磁畴壁与斯格明子可逆的相互转换[63]Fig.3.The reversal conversion between magnetic domain walls and magnetic skyrmions[63].
基于磁畴壁和斯格明子的可逆转换,Zhang等[62]提出可以通过Y型轨道实现斯格明子复制和融合.图4(a)和图4(b)分别展示了斯格明子的复制和融合过程.在图4(a)中,在输入端中输入一个斯格明子,随着驱动电流的注入,斯格明子在较窄的轨道中转换为一对磁畴壁.通过Y型交叉点之后,一对磁畴壁分化为两对磁畴壁,进而在输出端输出两个斯格明子,实现了斯格明子的复制.从图中也可看出,斯格明子数Q从1变到2.在图4(b)中,在输入端输入两个斯格明子,受电流的驱动,两个斯格明子分别进入较窄的纳米轨道并转换成两对磁畴壁.在Y型交叉点处,两对磁畴壁融合为一对磁畴壁,最后在输出端输出一个斯格明子,实现了斯格明子的融合.斯格明子数Q也从2变到1.
基于磁斯格明子的复制和融合,逻辑或门和逻辑与门就可以实现.图5为基于斯格明子的逻辑或门运算示意图.或门的操作包括:0或0=0,1或0=1,0或1=1,1或1=1.在基于斯格明子逻辑门的计算中,0代表不存在斯格明子,1代表存在一个斯格明子.0或0=0既没有输入,也没有输出.在图5左栏中,输入端A输入为1,输入端B输入为0,此时仅考虑从A端输入一个斯格明子.当A端输入的斯格明子从宽的纳米轨道进入窄的纳米轨道时,它被转化为磁畴壁在窄的纳米轨道中传输,最终再次在宽纳米轨道的输出端被转化成一个斯格明子,实现了1或0=1的运算.同理,如图5中间一栏所示,当A端输入为0,B端输入为1时,输出端为1,即输出一个斯格明子,完成0或1=1的运算.1或1=1的实现基于图4(b),即两个斯格明子融合为一个的过程.如图5右栏所示,当A,B两端均输入1时,由于两对磁畴壁在Y型结点处融合为一对磁畴壁,最终输出端只输出一个斯格明子,即输出1,实现了1或1=1的逻辑运算.
与门的操作也可以通过类似于或门的装置来实现.与门的逻辑操作包括:0与0=0,1与0=0,0与1=0,1与1=1.与门的0与0=0和1与1=1操作和或门的相同,不同的是1与0=0和0与1=0操作.图6显示了基于斯格明子的逻辑与门操作.当A端输入为1,B端输入为0时,在A端输入的斯格明子从宽的纳米轨道进入窄的纳米轨道时,它被转化为一对磁畴壁.这对磁畴壁随后在中间较宽的纳米轨道处被转化为一个麦纫[64].麦纫是一类附着于纳米轨道边缘的拓扑保护态,它的斯格明子数为0.5.最终这个麦纫在中间较宽的纳米轨道的右上角湮灭.这样就实现了逻辑与门1与0=0的操作.同理,0与1=0的逻辑操作实现于图6中间一栏.图6右栏展示的是逻辑与门1与1=1的操作,它的原理和逻辑或门的相同.因此,利用上述两种设计,就可以实现基于斯格明子的逻辑或门和与门.

图4 斯格明子的复制和融合[62] (a)斯格明子的复制;(b)斯格明子的融合Fig.4.Duplication and merging of skyrmions[62]:(a)The duplication of a skyrmion;(b)the merging of skyrmions.
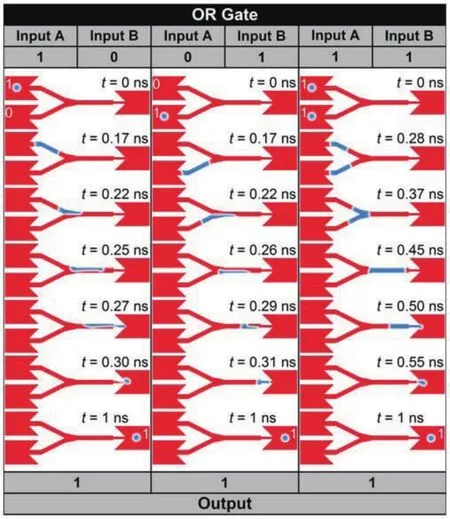
图5 斯格明子逻辑或门操作示意图[62]Fig.5.Illustration of skyrmions logical OR operation[62].
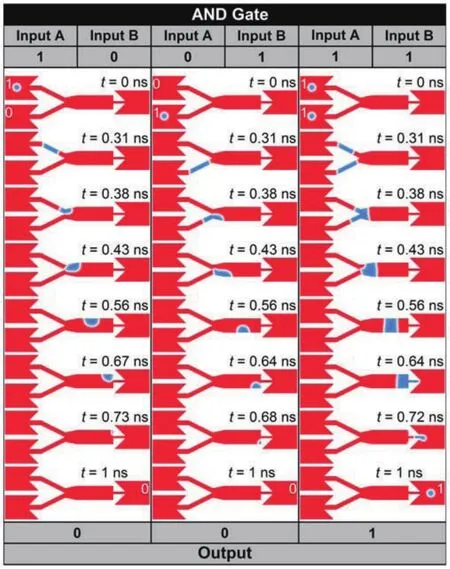
图6 斯格明子逻辑与门操作示意图[62]Fig.6.Illustration of skyrmions logical AND operation[62].
4 基于斯格明子的类晶体管器件
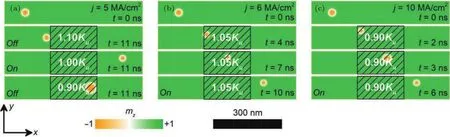
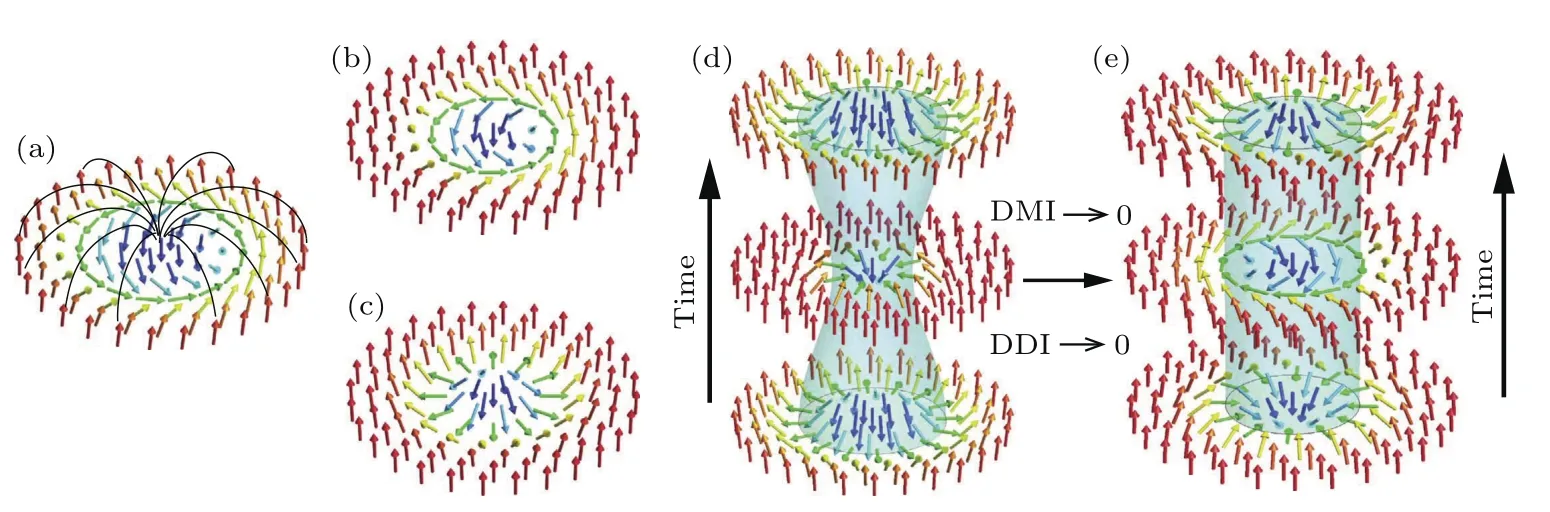
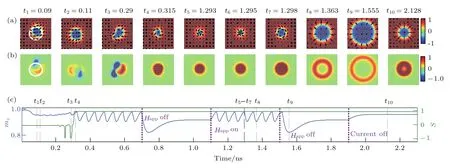
磁斯格明子还可以用于构建类晶体管器件[65],如图7所示,磁斯格明子最先由位于纳米轨道左侧的磁性隧道结(MTJ)写入,随后在自旋极化电流的驱动下向右侧移动,最后右端可利用隧穿磁电阻效应(TMR)探测斯格明子.其中,纳米轨道中部(200 nm 图7 基于斯格明子的类晶体管示意图[65]Fig.7.Design of the skyrmion transistor[65]. 磁斯格明子类晶体管器件有两个工作状态,关闭和开启.在关闭状态中,电场和自旋极化电流同时开启,电场改变了电压门区域的PMA,在纳米轨道中形成能量势垒,致使斯格明子无法通过.在开启状态中,当自旋电流是开启状态而电场是关闭状态时Kuv=Ku,斯格明子可以在自旋电流的驱动下通过压控门,从纳米轨道的左端到达右端. 在不同的自旋电流与受电场控制的Kuv下,斯格明子在纳米轨道上的运动状态也有差异,如图8所示.图8(a)显示的是驱动电流j=5 MA/cm2时,门电路施加不同电压值的器件的状态.当门电路处于关闭状态时,Kuv=Ku.此时,由于纳米轨道上无势垒,斯格明子在电流的驱动下可以顺利地从通过压控门到达轨道右端.当门电路开启时,Kuv=1.10Ku.因为压控区域PMA值的改变,在轨道中造成一个势垒,导致斯格明子停在压控区域的左侧边界处.当压控区域PMA值为Kuv=0.9Ku时,在压控区域形成势阱,斯格明子可以通过左边界,但无法通过右边界.可以看出,当门电路处于关闭时,类晶体管处于开启的状态,斯格明子可以自由地通过压控区域.当电路开启时,由于轨道PMA值的改变形成势垒或势阱,斯格明子无法通过压控区域,此时类晶体管处于关闭状态.当门电路开启时,Kuv=Ku,此时也可以通过调节驱动自旋电流密度的大小去调节类晶体管的工作状态.在图8(b)中,门电路开启,Kuv=1.05Ku,自旋电流密度提高到j=6 MA/cm2,此时斯格明子在较强的自旋电流驱动下,可以通过压控区域.同理,当Kuv=0.9Ku时,将自旋电流密度增至j=10 MA/cm2,斯格明子则可通过压控区域,如图8(c)所示.除此之外,还可以通过改变材料的其他磁性参数来调节类晶体管的工作状态,例如DM相互作用系数.基于斯格明子的类晶体管在工作状态对尺寸依赖性比较小,类晶体管的尺寸从600 nm×100 nm×1 nm缩小到150 nm×50 nm×1 nm时,工作状态都不会受到影响,由此说明类晶体管具有良好的可微缩性. 图8 不同驱动自旋电流密度j和K u v时,类晶体管的俯视图[65] (a)j=5 MA/cm 2,K u v=1.1K u,1.0K u,0.9K u;(b)j=6 MA/cm 2,K u v=1.05K u;(c)j=10 MA/cm 2,K u v=0.9K u;颜色表示磁矩的面外分量的大小,黑色阴影区域表示压控区域Fig.8.The top-view of the nanotracks under different j and K u v in the voltage-gated region:[65](a)j=5 MA/cm2,K u v=1.1K u,1.0K u,0.9K u;(b)j=6 MA/cm 2,K uv=1.05K u;(c)j=10 MA/cm 2,K uv=0.9K u.The colour scale denotes the out-of-plane component of the magnetization.The black-line shadows rep resent the voltage-controlled PMA region. 与磁涡旋类似,磁斯格明子在自旋转矩或外场的激发下呈现呼吸模式或转动模式,可用于产生频率在1—100 GHz范围内[69−72]的信号.基于磁斯格明子的纳米振荡器具有可调性强的特点.磁斯格明子振荡的频率可通过电流密度、外场强度、样品尺寸等多个维度进行调控,因此,非常适合构建纳米级微波振荡器[73−75]. 通过微磁模拟和解析分析发现,在DM相互作用下,注入垂直电流时磁斯格明子呈现出很强的呼吸模式,磁斯格明子的半径随时间呈周期性变化(见图9(d))[71].当偶极相互作用和DM相互作用消失时,斯格明子在布洛赫型(图9(b))和奈尔型(图9(c))之间周期变换,但尺寸不随时间变化,如图9(e)所示.图10显示了动态斯格明子的形成过程.首先,磁孤子在样品中成核,随着电流的持续注入,动态斯格明子形成,并呈现出稳定的呼吸模式,如图10所示.当外场消失或者出现时,呼吸模式也随之消失或者出现.当同时关闭外场和电流时,静态的斯格明子稳定存在于样品中.磁斯格明子的呼吸模式具有可调范围广和稳定性高等特点(见图11).图11(a)显示在施加不同外场和电流密度时,样品中最终可能出现的五种状态,包括磁矩朝上或朝下的铁磁态、磁孤子、动态斯格明子和静态斯格明子.从图中可以看出,在很大范围内动态斯格明子都可形成.图11(b)显示了动态斯格明子的稳定性.图11(b)中的态是以动态斯格明子为初始状态,施加不同的外场和电流密度,最终在样品中稳定存在的态.从图11可以看出,磁斯格明子不仅可以在大范围参数内达到稳定的振荡,并且在外部条件发生变化时还可以保持稳定的振荡.研究表明,斯格明子不仅具有很强的稳定性,而且在强磁场作用下,动态频率可以达到更高[76],这也使得动态斯格明子在宽频带微波应用中更具有吸引力.相比于基于涡旋结构的自旋转矩振荡器,基于斯格明子的自旋转矩振荡器的优势在于它对外部扰动不敏感,能产生更加稳定可靠的信号. 图9 不同机制下的磁斯格明子[71](a)磁斯格明子泡(skyrmion bubble),由偶极矩相互作用导致,尺寸远大于由DM相互作用稳定的磁斯格明子;(b),(c)由DM相互作用稳定的磁斯格明子;(b)布洛赫型,(c)奈尔型;(d)动态斯格明子,在偶极矩相互作用与DM相互作用下,斯格明子的直径周期性变化,呈现呼吸模式;(e)无偶极相互作用、DM相互作用与奥斯特场下,斯格明子均匀进动,呼吸模式消失Fig.9.Different skyrmion stabilization mechanism s[71]:(a)Askyrmion bubble stabilized by dipolar interactions;its size typically exceeds that of skyrmions stabilized by DM interactions;(b),(c)DM interactions stabilized skyrmions:(b)B loch type and(c)Neel type;(d)dynamically stabilized magnetic skyrmion(DS),in the presence of dipolar interactions and DM interactions,the skyrmion diameter varies periodically in time(breathing);(e)for vanishing dipolar interactions and DM interaction,the skyrmion precesses uniformly and breathing disappears. 图10 动态斯格明子的成核[71] (a)不同时刻对应的磁矩结构;(b)不同时刻对应的拓扑密度分布;(c)样品磁矩垂直分量的平均值m z和斯格明子数随时间的变化Fig.10.Nucleation and field toggling of a DS[71]:(a)The top view of the spin structure at selected simulation times;(b)the topological density at the same times;(c)the time trace of the out-of-plane magnetization component m z averaged over the simulation area and time trace of the skyrmion number(green). 此外,斯格明子转动模式也可以用来构建纳米振荡器[77,78].在这类振荡器中,通过注入自旋极化电流,利用斯格明子周期性的位置变化来产生信号.振荡的频率可以通过改变电流密度以及磁性纳米盘的半径进行调控,也可以通过利用多个斯格明子同时工作来提高振荡频率. 图11 动态斯格明子的稳定性[71] (a)施加不同外场和电流密度时的成核结果;(b)动态斯格明子在不同电流和场强下的稳定性;(c)不同状态的示意图,空心圆圈代表磁孤子,彩色实心圆圈代表动态斯格明子,绿色实心圆圈代表静态斯格明子,红色和蓝色方框分别代表磁矩朝上和朝下的铁磁态Fig.11.Stability of DS[71]:(a)Nucleation results at different fields and currents;(b)sustainability of the DS over a very wide range of current and field;(c)the schematic representation of different states.A drop let is rep resented by hollow circle;a DS is rep resented by filled rainbow circle;a static skyrmion is rep resented by green filled circle.The red and blue squares represent the upward and downward orientations of all the spins,respectively. 本文主要介绍了近年来基于磁斯格明子的器件和相关应用的研究成果和进展.首先简要说明了如何运用不同状态的斯格明子对二进制数据元进行表达,包括分别利用斯格明子的面外和面内磁矩分布结构.携带信息的斯格明子可直接用于存储和计算,具体应用可体现在基于磁斯格明子的赛道存储器和逻辑计算器件.通过结合赛道存储器与逻辑计算器,人们可继而设计出同时具备存储和计算功能的磁性器件.同时,利用磁性材料各向异性可被电压控制的特性,磁斯格明子可应用于设计类晶体管功能器件.另一方面,磁斯格明子也可应用于微波器件,如基于动态磁斯格明子的纳米微波振荡器.以上这些基于磁斯格明子的器件只是大量基于磁斯格明子应用中的具有代表性的例子.最近两年来,已有相关理论研究指出磁斯格明子还可用于更多新颖的应用,如基于磁斯格明子的仿神经元计算器件[79,80]和量子计算器件等.相信在不久的将来,我们将会看到多数斯格明子的相关研究队伍的研究焦点从基础理论和实验研究转向实际应用研究,也会因此看到更多基于磁斯格明子应用的提出和制备.磁斯格明子是否能最终商业化,将取决于未来几年内基于磁斯格明子应用研究的成果和水平.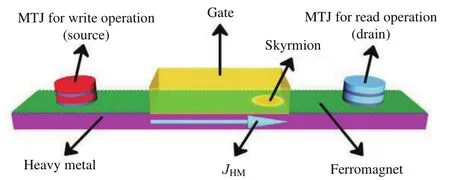
5 基于斯格明子的纳米振荡器

6 总结与展望

