轴向多光阱微粒捕获与实时直接观测技术∗

王玥 梁言生 严绍辉 曹志良 蔡亚楠 张艳 姚保利 雷铭

1)(中国科学院西安光学精密机械研究所,瞬态光学与光子技术国家重点实验室,西安 710119)

2)(中国科学院大学,北京 100049)

传统的光镊技术使用单个物镜同时进行光学捕获与显微成像,使得捕获与成像区域被限制在物镜焦平面附近,无法同时观察到沿光轴方向(即Z向)捕获的多个微粒.本文提出一种轴平面(X Z平面)Gerchberg-Saxton迭代算法来产生沿轴向分布的多光阱阵列,将轴平面成像技术与光镊结合,实现了沿轴向对二氧化硅微球的多光阱同时捕获与实时观测.通过视频分析法测量了多个二氧化硅微球在轴向光镊阵列中的布朗运动,并标定了光阱刚度.本文提出的轴向多光阱微粒捕获与实时观测技术为光学微操纵提供了一个新的观测视角和操纵方法,为生物医学、物理学等相关领域研究提供了一种新的技术手段.

1 引 言

自1986年Ashkin等[1]发现光场梯度力可捕获微小电介质粒子进而提出光镊概念以来,光镊技术已被广泛应用于生物学[2−5]和物理学[6−9]等研究领域.例如,在生物医学领域,它可以用来研究活体细胞和生物大分子的个体行为;在原子物理研究中,它可以用来捕获和冷却原子,研究玻色-爱因斯坦凝聚.利用衍射光学元件调制入射光的波前可以产生三维光阱阵列,同时对多个微粒进行复杂的三维空间微操纵[10].

微粒的三维空间动态微操纵使光镊技术在实际研究中具有极高的应用价值.但传统的光镊技术使用单个物镜同时进行光学捕获与显微成像,使得捕获与成像区域被限制在物镜焦平面附近,无法同时观察到沿轴向捕获和排列的多个微粒,限制了光镊捕获的应用.三维成像技术是可能的解决方法.以激光共聚焦技术为代表的点扫描显微成像技术利用高度聚焦的激光束对样品进行逐点扫描,激发出的荧光信号经过探测孔滤波后被光电倍增管探测收集,最后将所有信号重新组合生成一个三维图像.这种方法成像速率较低,不满足光镊快速成像的需要[11].以结构光照明显微[12]、光片显微[13]为代表的宽场成像技术可以快速获取样品的三维信息,但需沿光轴(Z)方向逐层拍摄样品的多个横平面(XY平面)二维图像,再提取轴平面(XZ平面)的信息,仍不满足光学捕获的实时成像要求.2007年,牛津大学的Wilson等[14,15]提出了一种可以实现快速三维成像的远距离聚焦显微成像技术.该技术使用一对完全相同的显微物镜,利用两个物镜补偿第一个物镜引入的球差,因而可以在第二个物镜的焦区得到样品的完美实像,再使用一个平面镜对这个三维实像进行高速推扫便可以获得样品的三维实像.这种成像方法不需要移动样品,平移台的扫描速率可以达到千赫兹,成像速度大大提升.同时,远距离聚焦技术还可以实现快速轴平面成像和任意平面成像[16,17].2014年,牛津大学的Curran等[18]与Wilson团队合作,将远距离聚焦显微成像技术应用在全息光镊技术中,实现了多个微粒的三维捕获与实时成像.但集成后的成像系统需要三个高数值孔径物镜才可以实现三维成像,导致整个光学系统的透过率不高.另外高数值孔径物镜的视场很小,轴向的观测距离十分有限.

本文提出了一种直接观测轴平面的方法,并将此与全息光镊技术相结合,可以直接观察轴平面上微粒的操纵过程.为实现稳定的轴向多光阱捕获,本文提出了基于轴平面傅里叶变换的Gerchberg-Saxton(GS)迭代算法.与透镜光栅组合法等直接算法相比较,此算法具有更高的调制效率,所产生的沿轴向分布的多光阱阵列具有更锐利的强度分布.理论上,利用轴平面GS算法产生的点光阱具有理想的高斯强度分布;实验上,实现了对多个二氧化硅微球的轴向同时捕获与光阱刚度的标定.

2 轴平面多光阱产生的基本原理

全息光镊技术的核心是通过衍射光学元件来调制入射光的相位分布,使调制后的光场经物镜的傅里叶变换作用后在物镜的后焦面上形成所需的目标光场分布[19,20].随着光镊技术的发展,全息光镊技术不仅要求在物镜后焦面上产生光阱,而且要求光阱具有三维空间分布,特别是轴平面技术的发展要求可以实现在任一轴平面上产生所需要的光阱阵列.如图1所示,本文中所提到的Z方向为光轴方向;与光轴方向垂直的平面为XY平面,本文中称为横平面;与光轴方向平行的平面为XZ平面,本文中称为轴平面.

三维光阱阵列的产生可以采用光栅透镜叠加的方法[21,22],通过光栅相位因子可以控制光阱的横向移动,菲涅耳透镜相位因子可以控制光阱的轴向移动.该算法简单快速,但再现质量随光阱复杂程度的增加而急速下降.另一种常用方法是迭代算法[23,24],例如传统的三维GS算法.这种方法需要将三维目标场分割成多个横平面,然后通过GS算法分别计算每一平面光场的相位全息图,最后将所有全息图叠加合成,因此计算量巨大[25].为快速高效地产生特定的轴平面光场分布,本文提出一种直接调控轴平面光场强度分布的GS迭代算法,即轴平面GS算法.此算法具有很高的调制效率,所产生的多光阱阵列具有比直接算法更锐利的强度分布.同时,该算法的计算量要比三维GS算法的计算量小得多.

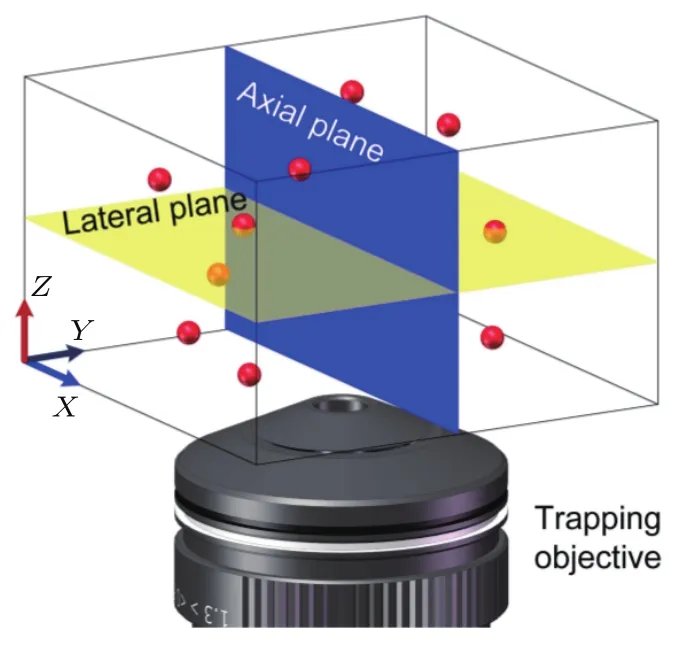
图1 捕获区域的空间坐标系示意图Fig.1.Schematic diagram of space coordinate system in trapping volum e.

轴平面GS算法是基于轴平面傅里叶变换公式的迭代算法,下面给出简单的推导过程.用ψH(kx,ky)和ψT(x,y,z)分别表示调制光场和目标光场,其中(kx,ky)和(x,y,z)分别表示SLM平面和焦区的坐标.根据理查德沃尔夫衍射理论[26],焦场可以写为

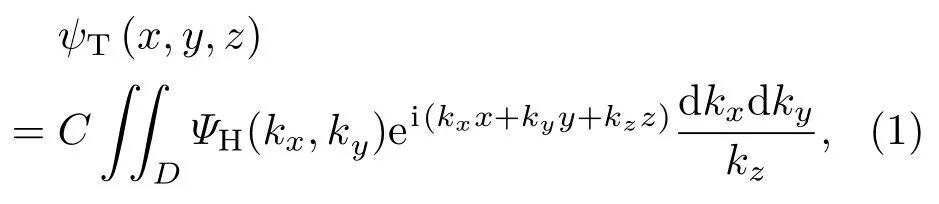
这里C是常数,(kx,ky)=k(u/fv/f)是横向波数,k和f表示波数和焦距,z=0表示焦平面.纵向波数与横向波数满足关系积分区域为其中A表示捕获物镜的数值孔径.

下面对(1)式中的积分进行转换,使其更适合于轴平面快速傅里叶变换(axial-plane Fourier transform,FT),即通过dkxdky=(k/|ky|)dkxdkz将积分变量改为kx和kz,令y=0,(1)式中的积分变为

横向波数ky满足为积分区域.变换后的轴平面上的光场ψT(xz)被表达为变量kx和kz的角谱积分,可以通过FT来计算.但(2)式中的角谱函数是ψH(kx,ky)和ψH(kx,−ky)之和,即ψH分别在ky>0和ky<0区域的值,而(2)式中积分项的傅里叶逆变换不足以明确定义所以为了明确定义,我们假设ψH关于ky对称,即,角谱函数ψH(kx,ky)和加载到空间光调制器上的调制光场可以就此确定,从而得到轴平面上的焦场ψT(x,0,z).

基于(2)式中的积分变换,通过调制输入光场ψH(kx,ky)便可以产生设定的轴平面焦场ψT(x,0,z).将该变换应用到经典的GS算法中,便可以快速、高效地在轴平面上直接产生任意光场.

为了验证轴平面GS算法的有效性,我们对比了这种算法与基于菲涅耳透镜的直接算法的理论光场结果,如图2所示,所用聚焦透镜的数值孔径为0.95.图2(a)给出了基于菲涅耳透镜组合的直接算法的结果,可以看出焦面上光阱(光阱1和3)再现效果良好,但离焦光阱(光阱2和4)的再现质量非常差.图2(b)和图2(c)所示的轴向一维强度曲线清晰地反映了这种现象:离焦光阱的最大强度虽与中间光阱一致,但其分布不再是高斯形状,而且光斑有明显的拉长和不对称性.更糟糕的是,“幽灵光阱”的存在降低了光场调制效率.图2(d)所示的利用轴平面GS算法得到的2×2点阵光阱都具有很高的质量,即使是在离焦状态下.图2(e)和图2(f)所示的轴向一维强度曲线显示出每一个光阱都保持了预期的高斯分布,而且最大强度基本一致.因此,相比于基于菲涅耳透镜和闪耀光栅的直接算法,轴平面GS算法可以更为高效、高质量地产生轴平面光阱阵列.

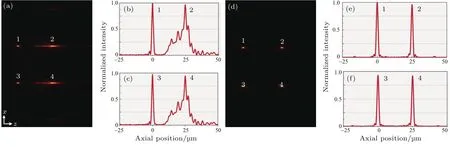
图2 基于菲涅耳透镜组合的直接算法与轴平面GS算法计算轴向点阵分布的结果比较 (a)基于菲涅耳透镜组合的直接算法计算的轴向点阵分布结果;(b)图(a)中的光阱1,2的轴向一维强度曲线;(c)图(a)中的光阱3,4的轴向一维强度曲线;(d)轴平面GS算法计算的轴向点阵分布结果;(e)图(d)中的光阱1,2的轴向一维强度曲线;(f)图(d)中的光阱3,4的轴向一维强度曲线Fig.2.Comparison of results of the axially distributive optical trap array generated by the superposition of Fresnel lens and the axial-plane GS algorithm:(a)Results from the superposition of Fresnel lens;(b)the axial intensity curves of optical traps 1 and 2 in(a);(c)the axial intensity curves of optical traps 3 and 4 in(a);(d)results from the axial-plane GS algorithm;(e)the axial intensity curves of optical traps 1 and 2 in(d);(f)the axial intensity curves of optical traps 3 and 4 in(d).

3 实验结果

3.1 实验装置

图3为轴向多光阱捕获与实时观测系统的光路示意图.波长为1064 nm,功率为2 W的连续Nd:YAG固体激光器(P/N:FB-1064,RGBLase LLC,美国)发出的线偏振光,经透镜1(焦距为10 mm)和2(焦距为100 mm)扩束准直和三角反射器后,进入反射式纯相位型液晶SLM(PLUTO NIR-II,Holoeye Inc.,德国)进行调制相位.由透镜3和4(焦距均为200 mm)组成的4f系统将调制后的光束中继到高数值孔径物镜1(40×,NA0.95)的入瞳,然后聚焦到样品溶液里对微球进行捕获和操控.样品池微管(Vitro Tube#8280-50,VitroCom Inc.,美国)中的二氧化硅荧光小球(488/515,BaseLine Inc.,中国)在波长为470 nm的发光二极管(LED)光源(DC4100,Thorlabs,美国)的激发下发射出的荧光,经45◦微棱镜反射后被物镜2(20×,NA0.45)收集,再经二向色镜滤波后,由透镜6(焦距为300 mm)会聚成像在相机2(1280 pixels×1024 pixels,5.3×5.3µm2/pixel,60 fps,8 bits,Thorlabs Inc.,美国)上. 横平面的荧光信号被物镜1收集,经二向色镜滤波后,由透镜5(焦距为200 mm)会聚成像在相机1(1280×1024 pixels,5.3×5.3µm2/pixel,60 fps,8 bits,Thorlabs Inc.,美国)上.利用相机1和2可以同时跟踪粒子的XY平面和XZ平面的位置信息,进而对光阱刚度进行标定.

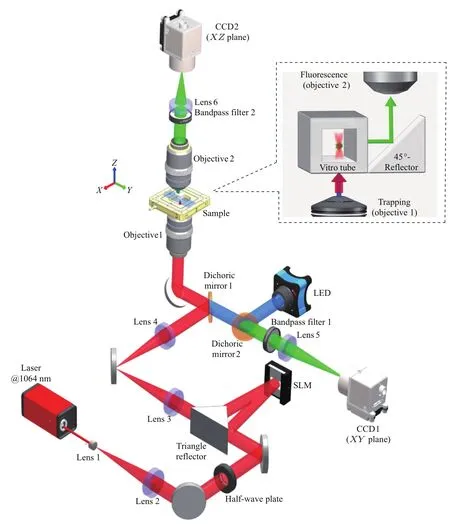
图3 基于45◦微反射棱镜的轴平面成像与光学捕获显微系统光路图Fig.3.Optical layout of simultaneous axial plane imaging and optical trapping system based on a miniature 45◦reflector.

3.2 结果与分析

3.2.1 轴平面与横平面同时成像

本文所搭建的基于45◦微反射棱镜的轴平面成像与光学捕获系统可以实现在横平面和轴平面同时对微操纵过程进行跟踪.为证明此功能,我们控制单个点光阱进行了三维动态微操纵实验.图4所示是直径为5µm的二氧化硅微球在横平面和轴平面的动态微操纵过程,其中箭头为微球的移动方向.当微球在焦平面沿X方向移动时(t=0—1 s),我们可以在横平面(图4(a))和轴平面(图4(b))同时追踪微球.当微球离开焦平面时(t=3 s),由于物镜景深有限,横平面的成像结果失去了微球的踪迹,不过我们依然可以在轴平面上观察到微球.图4(c)给出了微球在轴平面上的运动过程.上述结果证明了本文所搭建的系统可以同时在横平面和轴平面成像和跟踪微球的能力.

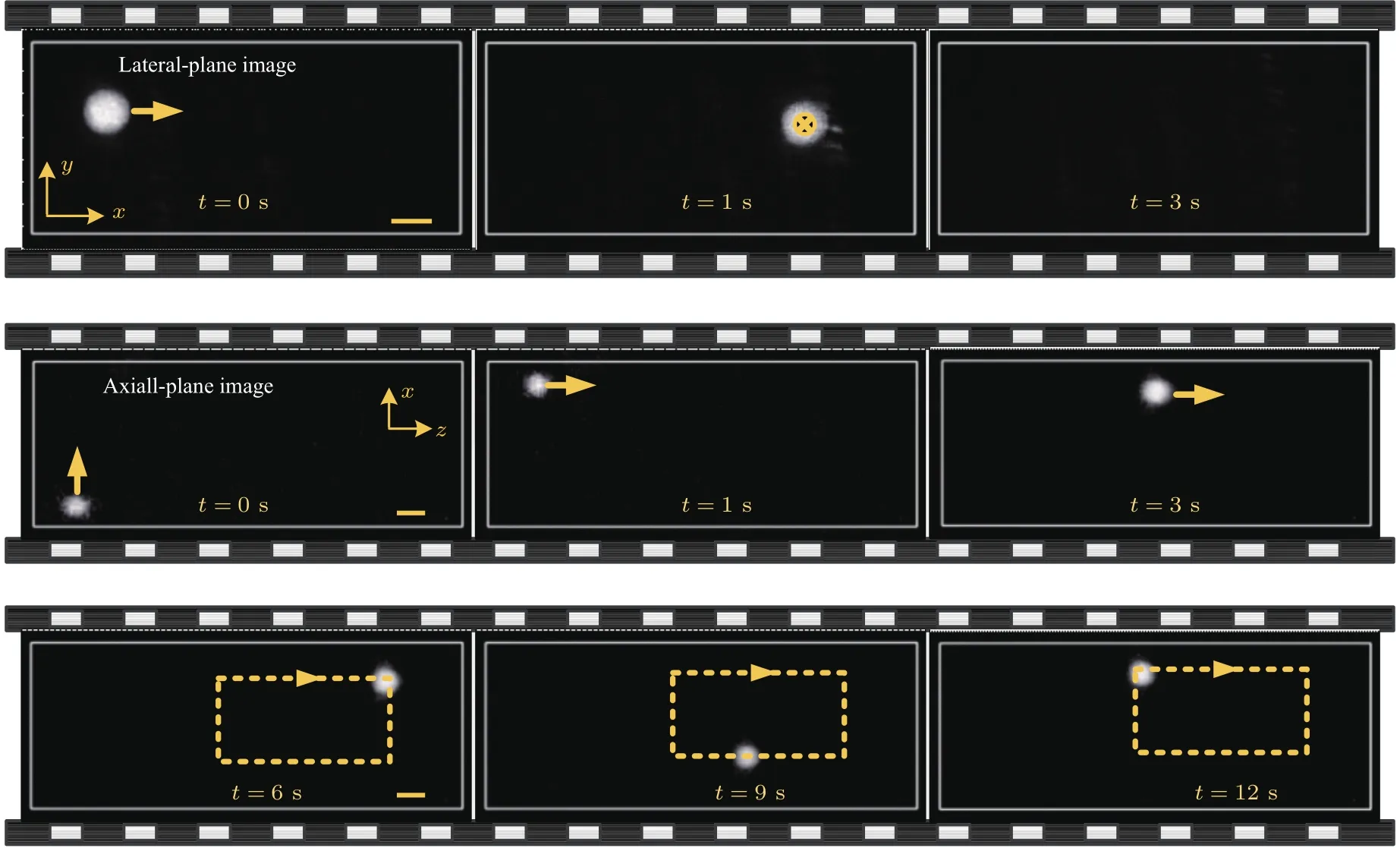
图4 在横平面和轴平面同时观测微球的动态微操纵过程 (a)横平面图像;(b),(c)轴平面图像;标尺=5µmFig.4.Observation of dynamic micromanipulation of microspheres in the lateral and axial planes simultaneously:(a)Lateral-plane images;(b),(c)axial-plane images.Scale bar=5µm.

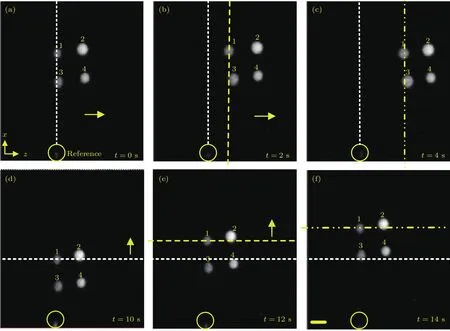
图5 轴平面同时捕获四个二氧化硅微球 (a)—(c)微球整体沿Z方向移动;(d)—(f)微球整体沿X方向移动;标尺=10µmFig.5.Simultaneous trapping of four silica microparticles in the axial plane:(a)–(c)The whole movement of microparticles in Z direction.(d)–(f)the whole movement of microparticles in X direction.Scale bar=10 µm

3.2.2 轴平面多光阱捕获与动态操纵

本文所提出的轴平面GS算法可以直接在XZ平面调制产生光阱阵列.作为例子,我们研究了2×2点光阱阵列的轴平面捕获与动态操纵.相邻两个光阱的间距设为25µm,数值模拟得到的光场强度分布如图2(d)所示.利用该光阱阵列的捕获验结果如图5所示,其中箭头表示微球的移动方向,虚线为微球1的位置,圆圈中的物体是参照物.通过刷新提前设计好的全息图,我们可以动态控制被捕获的二氧化硅微球在轴平面上沿Z和X方向移动,如图5(a)—(c)和图5(d)—(f)所示.在图5(a)—(c)中,不同的虚线表示微球1沿Z方向移动时的位置.由图5(a)—(c)可以看出,微球在沿Z方向移动的过程中保持着被稳定捕获的状态.同样,在图5(d)—(f)中,微球在沿X方向移动的过程中也处于稳定束缚状态态.微球在轴平面上的移动过程证明了利用轴平面GS算法产生的四个光阱对微球具有三维稳定捕获能力.

3.2.3 光阱刚度的标定

光阱的力学特性对于光学捕获的应用具有重要意义.通过标定光阱的力学特性,光镊可以对微观粒子实施可控的作用力和操纵.要测量微粒在光阱中的受力,首先需要标定光阱刚度,而标定光阱刚度首先要获取粒子的布朗运动信息.一种方法是利用四象探测器快速跟踪粒子,但每次只能跟踪一个粒子.另一种方法是视频跟踪法,可同时跟踪多个粒子的运动,缺点是跟踪速度较慢.不过对于本文所研究的轴向多光阱捕获,视频跟踪法显然是最好的选择.

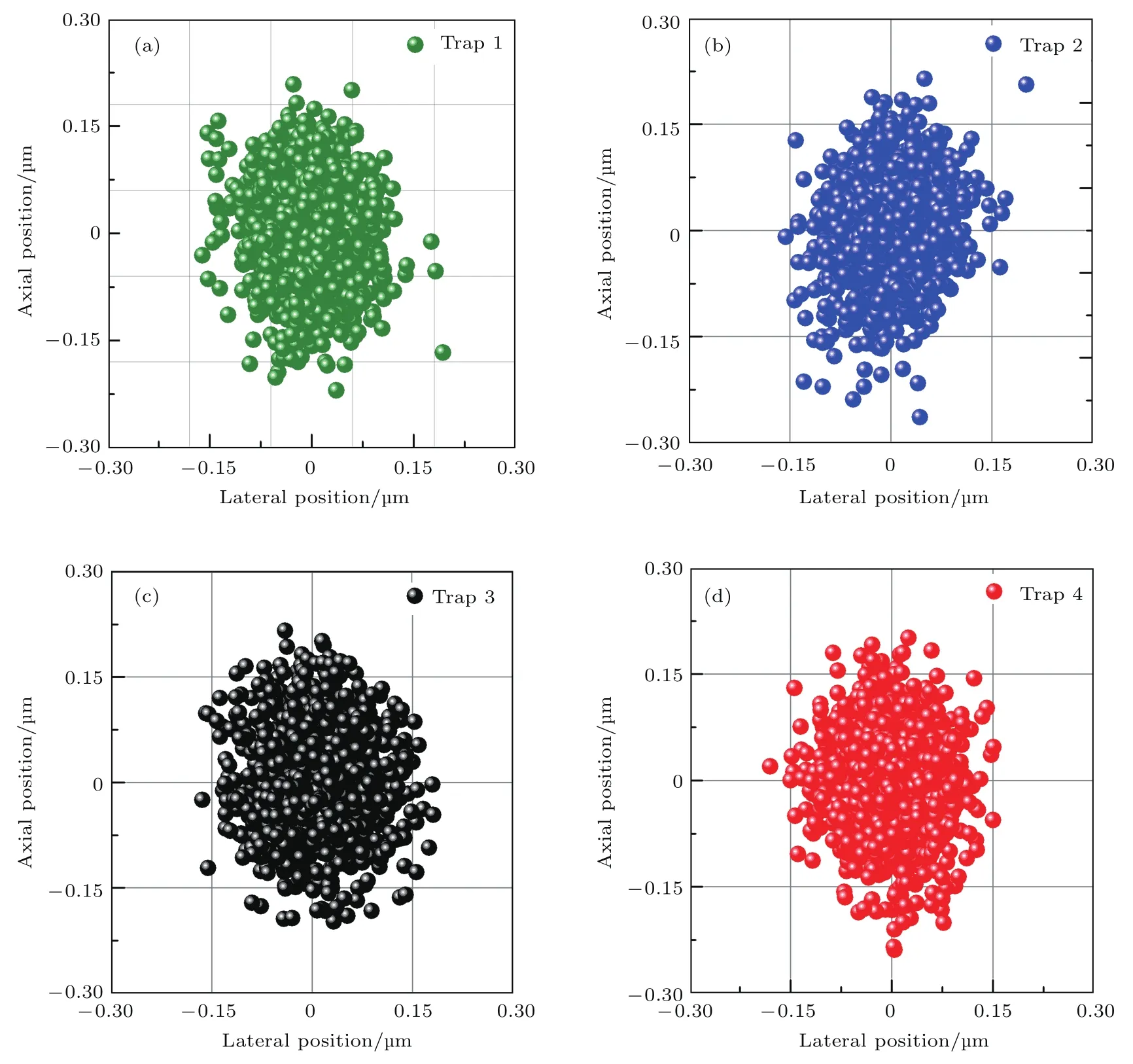
图6 轴向四个光阱的轴平面微球运动位置分布图 (a)光阱1;(b)光阱2;(c)光阱3;(d)光阱4Fig.6.Position charts of the trapped beads in the axial plane:(a)Trap 1;(b)trap 2;(c)trap 3;(d)trap 4.

表1 轴向2×2光阱阵列的光阱刚度标定结果Table 1.The calib rated stiffness of 2×2 axial optical trap array.

通过轴平面实时成像技术可以记录微球的轴平面运动视频.利用中心定位算法求出视频每一帧中微球的位置,将这些位置统计叠加起来便可以得到微球的位置分布信息.由图6给出的微球位置分布图可以看出,微球1和2的位置分布相对集中,横向位置主要集中在[−0.1,0.1]µm,轴向位置主要分布在[−0.15,0.15]µm.粒子3和4的位置分布较为分散,横向位置主要分布在[−0.15,0.15]µm区间,轴向位置主要分布在[−0.17,0.17]µm区间.由此可以判断,光阱1和2的刚度比3和4的稍大.

进一步通过热力学噪声法对光镊的光阱刚度进行了标定[27].微球在光阱中的布朗运动位移量x满足均分定理:

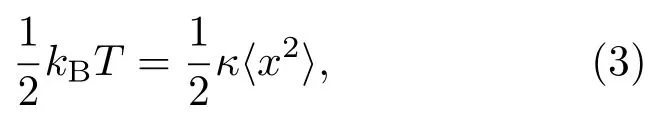
其中,kB为玻尔兹曼常数,T为绝对温度,x为被捕获微球偏离其平衡位置的距离(一维),κ为光阱刚度.根据图6的微球布朗运动信息可以计算得到各个微球位置偏移量的均方差,代入(3)式可以计算得到四个光阱的横向与轴向光阱刚度,结果如表1所引,κX和κZ分别表示横向光阱刚度和轴向光阱刚度,实验温度为20◦C.四个光阱刚度相差不大,光阱1和2的横向和轴向光阱刚度分别是光阱镊3和4的1.2倍和1.1倍.这是由于通过轴平面GS算法产生的2×2光阱阵列中的光阱强度分布相差不大,光阱1和2的峰值强度相对较高,光阱3和4的相对较低.

4 结 论

本文提出了一种直接观测的轴平面成像技术,可以实现对样品轴平面的清晰成像.将全息光镊技术与直接轴平面成像技术相结合,可以直接观察到轴平面上微粒的微操纵过程,解决了传统光镊系统由于使用单个物镜同时进行光学捕获与显微成像时,无法同时观察到沿光轴方向捕获多个微粒的问题.本文提出的轴平面傅里叶变换GS迭代算法可以快速、高效地直接在轴平面产生光阱阵列,而且所产生的点光阱都具有高斯强度分布,优于基于菲涅耳透镜的直接算法,实现了对多个二氧化硅微球的轴向同时捕获与监控,并标定了它们的光阱刚度.本文所提出的轴平面多光阱光学捕获和直接观测技术,拓展了光学捕获的功能,在生物医学、物理学等研究领域中具有潜在的应用前景.