基于遗传算法的动力总成悬置模态解耦及隔振性能优化

卢炽华， 刘永臣， 刘志恩， 周依帆， 张 磊

(1.武汉理工大学 现代汽车零部件技术湖北省重点实验室，武汉 430070；2.武汉理工大学 汽车零部件技术湖北省协同创新中心，武汉 430070；3. 欧源动力科技有限公司，武汉 430070；4. 同济大学 工程训练中心，上海 200092)

发动机是汽车的动力源，也是主要的噪声与振动源[1-2]。动力总成所产生激励若不能有效地被隔离，会通过多种传递路径传递到车身，产生振动和噪声，进而传递到驾驶室内，对乘客的乘坐舒适性产生影响。动力总成悬置的设计和优化严重影响整车NVH性能[3]。

良好的发动机悬置对降低发动机振动幅度减少噪音，提高整车乘坐舒适性起着重要作用[4]，目前对动力总成悬置的优化方法主要有能量解耦法[5]、总传递力最小法[6]、移频法[7]。国内对悬置的优化，侧重基于能量解耦法选择适当的悬置安装位置、角度和三向刚度，进而达到合理配置动力总成刚体模态的固有频率和实现系统振动解耦程度的提高[8-9]。史文库等[10]在MATLAB平台采用遗传算法基于能量分布对悬置系统橡胶静刚度进行优化，并取得显著效果；吴杰等[11]通过改变悬置静刚度和安装位置对悬置刚体模态频率进行调整，进而使各阶模态频率分配更加合理；柯有恩等[12]在ADAMS软件中建立振动模型，并通过能量解耦法对悬置系统优化，改善悬置系统的隔振性能。以上研究多只针对悬置静刚度进行优化设计，而未考虑悬置非线刚度性设计要求。

本文针对某纵置汽油发动机车型原设计悬置隔振性能不达标的问题，通过MATLAB与Isight联合仿真，基于遗传算法对悬置系统的解耦率进行优化，并计算优化后悬置在通用28工况下的悬置变形位移，通过整车实验验证优化后悬置隔振性能。

1 动力总成悬置动力学模型及固有特性计算

1.1 动力总成悬置六自由度模型

相对于发动机和变速器，橡胶悬置刚度较低，在进行悬置的有关计算中，将动力总成简化为和车身连接的刚体，橡胶块则用三向刚度弹簧模拟[13]，动力总成及悬置简化如图1。

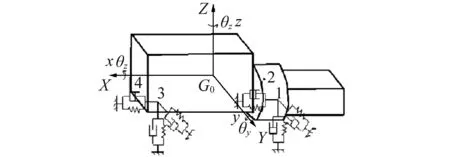
图1 悬置简化模型Fig.1 simplified model of suspension

动力总成质心坐标系G0XYZ中，X轴平行于曲轴方向，并指向发动机前端；Z轴平行于活塞运动方向并以向上为正方向；Y轴方向则由右手定则判断。取三向位移x,y,z和三向转角θx,θy,θz共六参数描述动力总成运动广义坐标。

文中所涉及车型为某整车厂研制的前置后驱式SUV，其发动机布置方式为纵置式，通过左悬置、右悬置、和后悬置对发动机进行支撑。其中，后悬置结构设计较为特殊，两个橡胶块分布于后悬置左右两侧，其结构见图2。

图2 后悬置结构图Fig.2 structure of rear suspension

后悬置中两个橡胶块相距180 mm，绕整车X方向和Z方向存在较大旋转刚度，三个线性刚度弹簧不足以描述后悬置刚度特性。因此，后悬置件在进行分析计算应拆分为两个悬置，即在进行固有频率计算以及解耦率分析时需要将动力总成悬置作为四点悬置处理，共需12根刚度弹簧对悬置橡胶进行简化。

1.2 动力总成悬置固有特性计算方法

进行悬置固有频率计算时，通过拉格朗日方法建立振动方程，系统的势能和动能通过变量形式表示。拉格朗日方程形式为：

(1)

式中：ET为系统动能；EV为系统势能；ED为系统耗散能；q为系统广义坐标；Q为系统所受广义力。由上述拉格朗日运动方程可求得悬置自由振动微分方程如下：

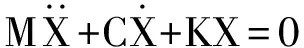
(2)

式中:M为系统质量矩阵；C为系统阻尼矩阵；K为系统刚度矩阵；X为广义坐标列向量。在进行动力总成的固有特性分析时，一般将振动系统简化为一个无阻尼自由振动系统，则振动微分方程简化为：

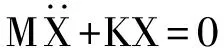
(3)

求解[K]-ω2[M]=0，可得到系统固有圆频率。假设式(3)的解为X=Aejωt,主振型方程见式(4)

(K-ωn2M)A=0

(4)

任何一个特征值ωnr2代入式(4)都可以得到一个相应的非零向量A(r),即主振型。

1.3 模态解耦率计算

在能量角度上，悬置系统100%解耦就是作用于该方向的激振力所做功，全部转化为系统沿该方向的能量，即沿着某坐标轴方向的激励只能激起该方向的振动。悬置系统的解耦程度用模态解耦率表示，模态解耦率的计算公式可用式(5)表示：

(5)

式中：Ai为系统第i阶主振型；(Ai)k为Ai的第k个元素和第i个元素；mkl为系统质量矩阵的第k行l列元素。

2 遗传算法介绍

遗传算法[14]由Holland于1975年提出，它是模拟自然选择和遗传学基理的生物进化过程的计算模型，是通过模拟自然进化过程搜索最优解的方法，遗传算法在组合优化、自适应控制等领域有较多应用[15-17]。

2.1 目标函数

悬置系统模态解耦率优化是约束条件下的最优解问题。基于遗传算法的目标函数的表达式为

(6)

式中:Wi是i阶能量加权因子；Tpi表示i阶模态主振方向能量百分比。

2.2 优化设计变量

悬置优化过程一般选取悬置安装位置、安放角度、橡胶静刚度等为设计变量。鉴于悬置安放空间限制，本文选取四个橡胶件的三向静刚度共12个变量进行优化。

2.3 优化约束条件

在各阶频率分配方面，动力总成悬置系统的各阶模态应避免车身刚体模态(1～4 Hz)和簧下质量跳动模态(15～18 Hz)，因此模态频率需要控制在4.5～15 Hz。为避免各阶模态重合，使模态频率间隔最小值设置为0.5 Hz。

在模态解耦率数值方面，理论上悬置各阶模态解耦率可达100%，但由于发动机布置空间和橡胶材料限制，现实中要求模态解耦率达100%很难实现。本文中，对纵置发动机较为关心的Z向和Rx向模态解耦率需达到85%以上，其他方向模态解耦率达80%视为满足设计要求。

3 悬置优化

通过Isight中集成MATLAB模块可以较为便捷地进行悬置解耦率优化。在Isight中完成参数变量、约束条件、优化目标等的设置即可进行基于遗传算法的参数优化，优化完成后需对优化结果进行筛选，以选出约束条件下的最佳悬置布置方案。

3.1 动力总成悬置基本参数

对动力总成悬置进行优化，首先需要计算出悬置各阶模态能量解耦率，其中动力总成质心位置、动力总成质量、转动惯量和悬置弹性中心位置、橡胶三向刚度等参数影响着模态解耦率，上述参数具体数值见表1和表2

表1 动力总成质心位置以及转动惯量参数

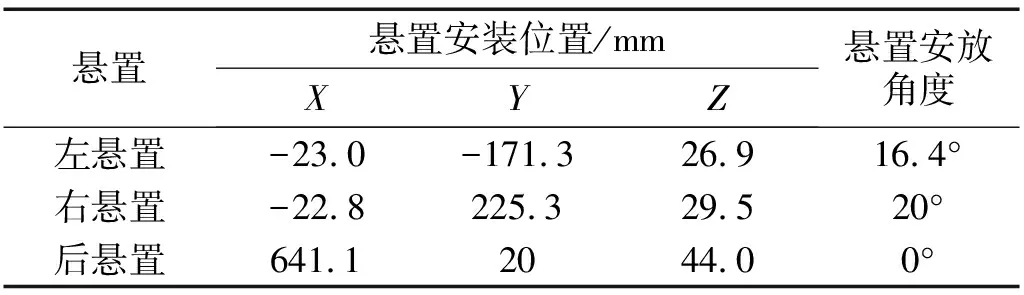
表2 原悬置安装位置以及安放角度

3.2 原悬置模态解耦率计算

表3是根据相关参数在动力学软件ADAMS中根据能量解耦理论获得的各阶模态能量分布。在纵置发动机较为关心的Z向以及Rx向解耦率分别为67%和57%，其他方向解耦率亦较差，远达不到悬置解耦率设计要求。

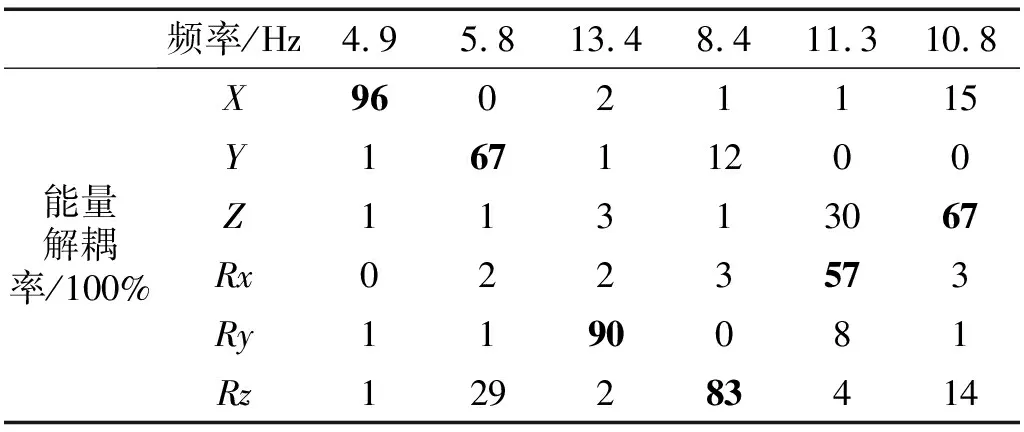
表3 原悬置能量解耦率

3.3 优化结果分析

通过Isight与MATLAB联合优化，悬置各阶模态能量解耦率均有提高。Z向和Rx向振动解耦率分别提至93.1%和87.4%，较原悬置解耦率提升幅度较大，其中Rz向解耦率稍有降低，但因为Rz向振动不是纵置发动机主要关心的振动方向且解耦率降幅较小，可忽略Rx方向模态解耦率降低所导致影响。在各阶模态频率分布方面，经过优化后的悬置各阶模态分配合理，优化结果符合要求，表4为优化后的悬置各阶模态解耦率分布表，表5为优化后的各悬置静刚度。

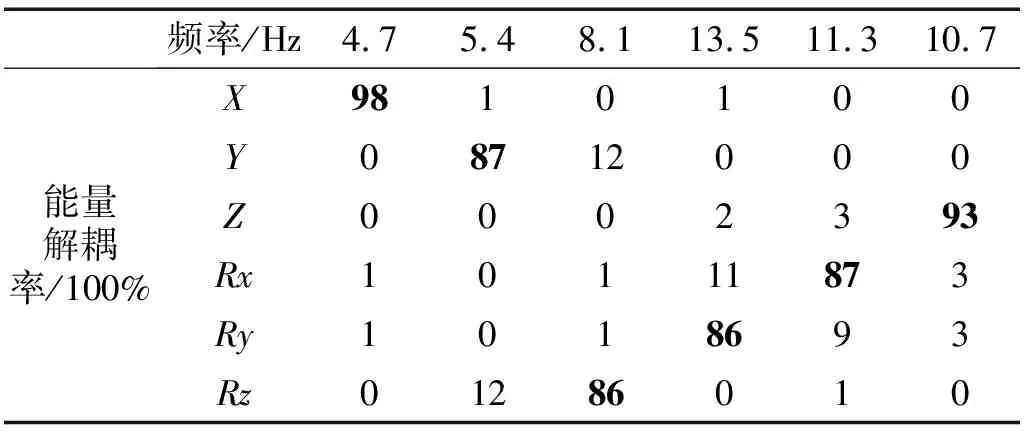
表4 优化后悬置各阶模态解耦率

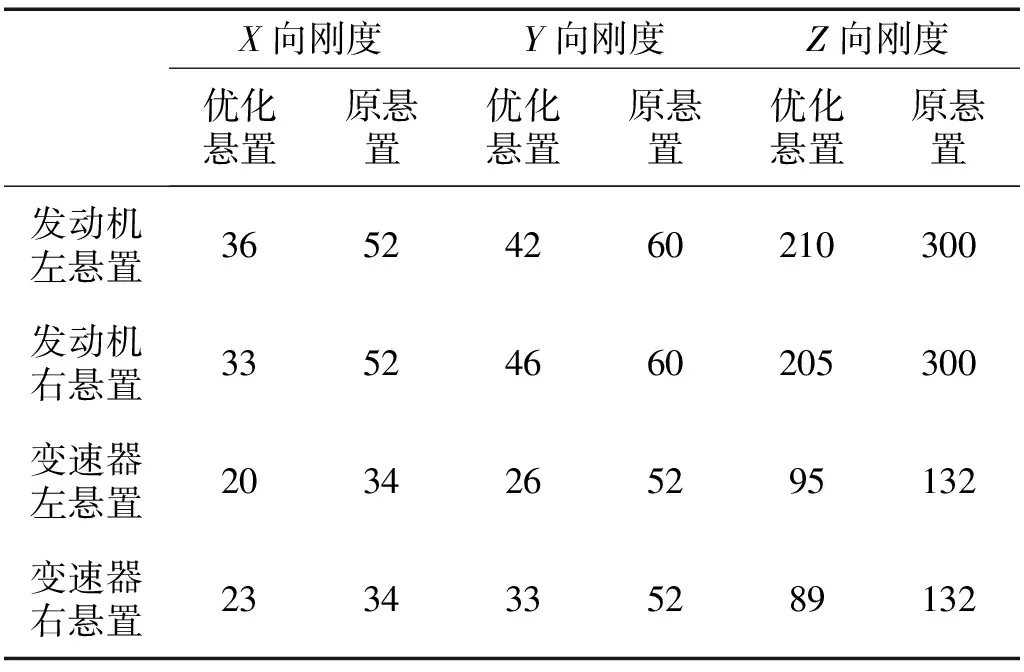
表5 优化前后悬置静刚度对比

4 整车实验

在悬置设计初期阶段，以悬置各阶模态频率分布和模态解耦率为主要评价指标，整车阶段，评价悬置系统隔振效果的主要指标是悬置隔振性能[18]，为验证上述经优化后悬置是否满足隔振要求，对新设计悬置进行整车隔振性能测试。

4.1 实验设备及方案

在前期悬置固有频率和模态解耦率计算阶段，后悬置被简化为两个三向刚度弹簧进行动力学建模，但考虑其结构整体性，隔振性能测试中将后悬置作为整体进行处理。本次实验共需笔记本电脑一台、数据采集仪一套、加速度传感器六个。将加速度传感器分别布置在悬置的主动侧和被动侧，通过LMS SCADAS数采设备采集各加速度传感器振动信号并传输到计算机，经过LMS TEST.Lab软件对数据进行处理可获得主被动侧时域下加速度响应曲线，图3为传感器在悬置上的布置位置。

图3 加速度传感器布置在悬置上的布置位置Fig.3 The station of acceleration sensor put on suspension

4.2 悬置隔振率测试结果分析

汽车怠速开空调以及怠速关空调两种情况下分别测量悬置主被侧加速度信号。主被动侧振动加速度不能直观反映出悬置隔振性能，通常采用悬置传递率来评价悬置隔振效果，传递率是主动侧振动数值与被动侧振动数值之比。传递率越大，悬置隔振效果越好，加速度的传递率用分贝形式表示为：

(7)

当隔振率大于20 dB，也就是从主动侧传递到被动侧的能量衰减10倍，悬置被认为是满足设计要求的。图4,5为原悬置与被优化悬置隔振率对比数据。原悬置在怠速开关空调工况下，各悬置隔振性能均不符合设计要求，经优化后，悬置隔振性能均有提高。

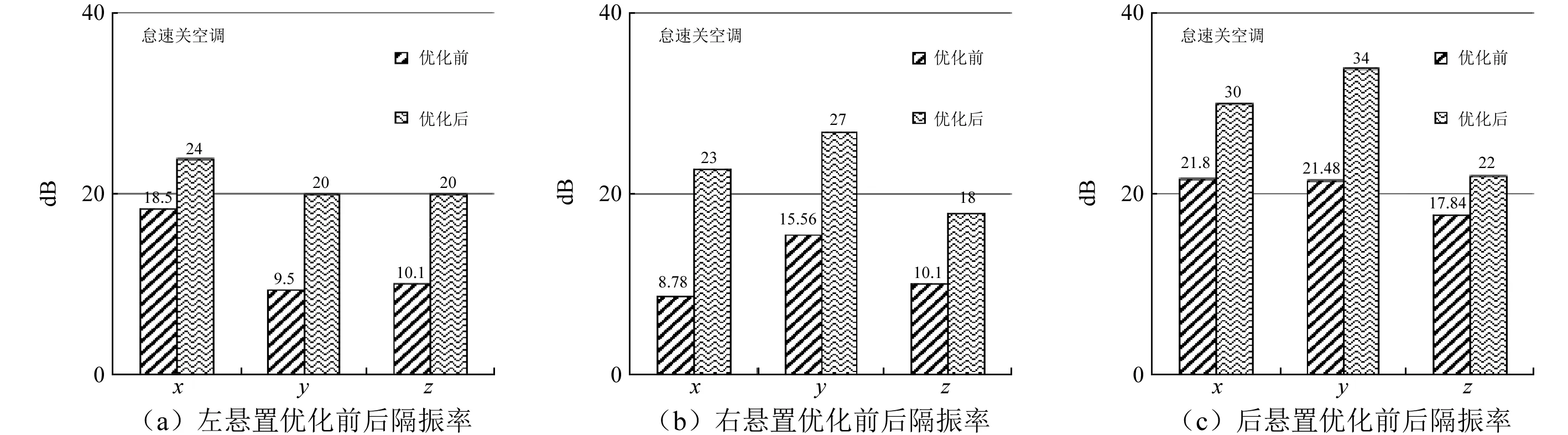
图4 怠速关空调工况下优化前后悬置隔振率Fig.4 Vibration isolation rate of suspension before and after optimization on the condition of idling with AC off

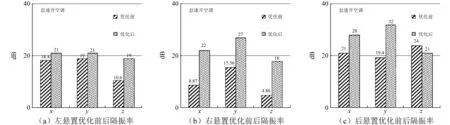
图5 怠速开空调工况下优化前后悬置隔振率Fig.5 Vibration isolation rate of suspension before and after optimization on the condition of idling with AC on

5 几种典型工况下悬置限位作用分析

合理的动力总成悬置系统不但需要满足解耦率和隔振要求，还要实现良好的限位作用。针对优化后悬置线性段静刚度，结合原有悬置非线性刚度设计，在ADAMS软件将悬置刚度进行非线性化处理，对优化后悬置进行北美通用28工况载荷仿真分析以判断悬置线性段以及非线性段刚度设计是否合理。动力总成质心各向最大位移以及最大偏转量见表6，表7列举出了工程经验获得的动力总成运动空间限值标准。

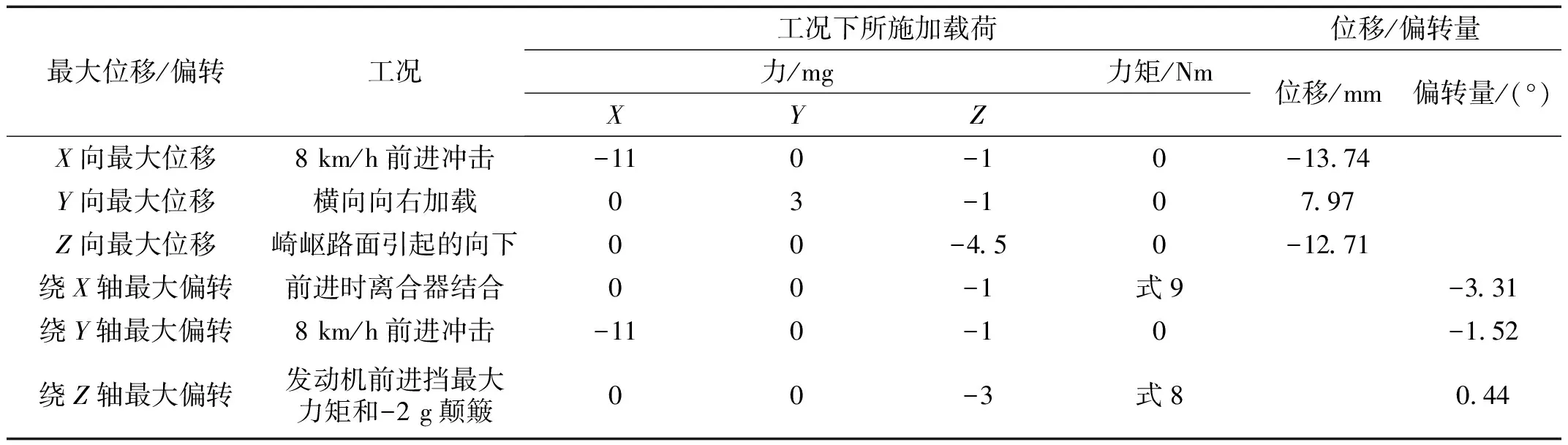
表6 动力总成质心在28工况下的最大位移及偏转

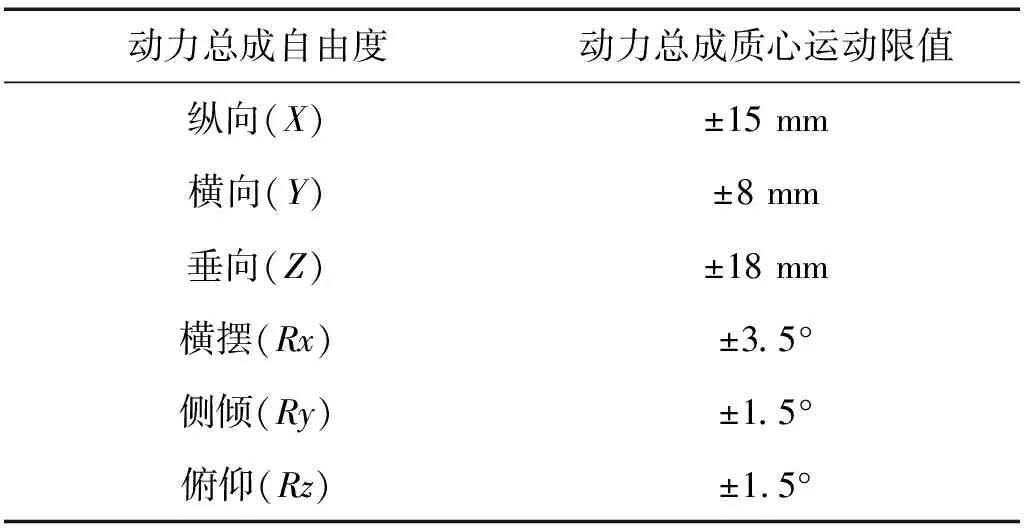
表7 动力总成运动空间限值

TWOT,Fr=TMETiiFDRfMF

(8)

TCLU,Fr=2.2TMETiiFDR

(9)

式中:TWOT=节气门全开力矩；TMET=发动机最大力矩；i=1档传动比；iRGR=倒挡传动比；iFDR=1；fMF=1.4

经仿真对比，在极限工况下悬置依然可以起到充分的限位作用，优化后的悬置能满足解耦率、隔振和限位要求。

6 结 论

(1)通过某国产SUV进行悬置隔振率测试，得出原悬置隔振效果不佳的结论。提出通过两个三向刚度弹簧模拟后悬置独特结构的方法，并建立动力总成悬置系统的多体动力学模型，计算原悬置固有特性和模态解耦率。

(2)针对原悬置各阶模态解耦率较低的特点，以解耦率为优化目标，以悬置安装位置和安放角度为优化变量，通过Isight与MATLAB联合优化，约束条件下求得最优解，进而改善悬置解耦率。

(3)对优化悬置进行隔振效果测试，相对于原悬置，优化后悬置能有效改善隔振性能，三个悬置各方向隔振率基本达到设计要求。

(4)结合原悬置非线性段刚度设计参数对优化后悬置进行通用28工况模拟仿真，仿真结果表明优化后悬置可满足限位要求。