高速列车乘坐舒适度评价的概率密度演化方法

刘章军， 张传勇， 齐东春

(1. 防灾减灾湖北省重点实验室(三峡大学)，湖北 宜昌 443002； 2. 三峡大学 土木与建筑学院，湖北 宜昌 443002)

科学技术的不断进步和社会经济的快速发展，为我国高速铁路的发展奠定了坚实基础。随着列车运行速度的不断提升，使得轨道不平顺的激励作用被放大，影响旅客乘坐的平稳性和舒适性。近年来，国内外学者在列车舒适度方面进行了大量研究，取得了一系列成果[1-8]。

轨道不平顺作为车辆-轨道耦合系统随机振动的主要外部激励源，其获取方法一般有两种：线路实测和数值模拟。由于线路实测工作量大、成本高、对设备要求高而受到限制，使得数值模拟被广泛应用。目前，常用的数值模拟方法有：逆傅里叶变换法[9]、三角级数法[10]、白噪声滤波法和二次滤波法[10]。为了在概率密度层次上描述轨道不平顺随机过程，本文采用谱表示-随机函数方法[11-13]，利用随机函数的约束形式能够有效地降低随机过程的随机度，从而实现用一个基本随机变量即可表达轨道不平顺随机过程的目的。

从狭义上讲，舒适度评价是指列车运行过程中由于车体振动对乘客影响的评价。陈祥等基于因子分析与层次分析方法建立了高速列车乘坐舒适度评价模型，通过确定旅客乘坐需求、生理和心理感受等因素的影响权重进行综合评价；王海涌等利用粗糙集和模糊分析相结合的方法对城际高速铁路舒适性进行了分析；国云鹏等基于建筑学振动烦恼率对高速列车的平稳性进行了分析；王海涌等基于ANP和VPRS理论，确定高速列车舒适性综合评价指标的权重。上述研究为高速列车乘坐舒适度评价提供了不同的方法。在随机动力系统分析方面，Li等[14-17]提出的概率密度演化理论可以获取随机响应的精细概率信息，在线性与非线性多自由度系统的随机动力反应分析、体系可靠度计算以及振动控制等方面取得了系统性研究进展。在本质上，轨道不平顺模拟的谱表示-随机函数方法与概率密度演化理论具有一致性，两者的结合可为车辆-轨道耦合系统的随机动力响应提供高效精确分析方法，实现旅客乘坐舒适度的精细化计算，进而为高速列车乘坐舒适度评价提供新的途径和方法。

1 谱表示-随机函数模拟方法

对于零均值的平稳随机过程X(t)， 假定其单边的功率谱密度为SX(ω)，ω为圆频率(rad/s)，则平稳随机过程模拟的谱表示为

(1)

式中： Δω为频率离散步长；N为频率截断项数；ω1和ωN分别为下截止频率和上截止频率，存在如下的关系

(2)

ωk=ω1+(k-1)Δω

(3)

在式(1)中， {Xk,Yk}(k=1,2,…,N)为一组标准的正交随机变量，满足如下的基本条件

E[Xk]=E[Yk]=0,E[XkYk]=0

(4a)

E[XkXl]=E[YkYl]=δkl

(4b)

式中：δkl为Kronecker-delta符号，E[·]为数学期望。

在式(1)中，如果令

(5)

式中：φk(k=1,2,…,N)为在(0,2π)上均匀分布且相互独立的随机变量。显然，式(5)满足式(4)的基本条件。

将式(5)代入式(1)中，即可得到经典的谱表示模拟方法[18]

(6)

一般地，式(1)称为基于正交随机变量的谱表示，式(6)称为基于随机相位角的谱表示。由于基于随机相位角的谱表示可以采用FFT算法，因此，在实际模拟中得到广泛地应用。

从上述推导过程中，可以发现基于随机相位角的谱表示是基于正交随机变量谱表示的一种特例，即通过在基于正交随机变量的谱表示中定义式(5)得到基于随机相位角的谱表示。显然，只要能够满足基本条件式(4)，还可以定义标准正交随机变量Xk和Yk的不同随机函数形式，从而得到不同类型的谱表示模拟公式。

事实上，式(5)可以理解为是对标准正交随机变量Xk和Yk施加的一种约束形式，从而使得式(1)中随机变量的数量2N减少为式(6)中的N。可见，通过施加某种约束条件可以有效地降低随机过程模拟的随机度(随机变量的数量)。

基于这一认识，如果对标准正交随机变量施加更强的约束条件，则可能极大地降低谱表示模拟公式中的随机变量数量。为此，将Xk和Yk(k=1,2,…,N)表达为概率分布已知的基本随机变量Θ的正交函数形式，即定义Xk=gk(Θ)，Yk=hk(Θ)， 其中gk(·)和hk(·)为确定性的正交函数式。在本文中，标准正交随机变量的随机函数定义为

(7a)

(7b)

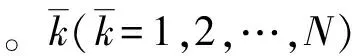
显然，式(7)定义的随机函数形式使得基于正交随机变量的谱表示模拟公式(1)中的随机变量数量2N减少为1。从而克服Monte Carlo模拟方法需要成千上万个随机变量的局限性，为复杂工程结构的随机动力反应分析提供基础。

2 轨道不平顺模拟

功率谱密度是表征平稳随机过程的轨道不平顺最常用统计函数。工程中常用空间频率fm(cycle/m)或ωm(rad/m)来表达轨道不平顺的功率谱密度。在轨道不平顺模拟时，则通常采用时间频率ft(cycle/s)或ωt(rad/s)来表达功率谱密度。它们之间的关系如下：

ωm=2πfm,ωt=2πft

(8a)

ft=vfm,ωt=vωm

(8b)

式中：v为列车运行速度(m/s)。顺便指出，时间频率的单位也可以表示为

cycle/s=Hz, rad/s=1/s=s-1

(9)

本文选用我国高速试验线谱作为轨道不平顺功率谱密度(七参数谱)，其表达式为[19]

(10)

式中：Sm(fm)为轨道不平顺功率谱密度， 其单位为mm2/(cycle/m)；fm为空间频率(cycle/m)；A～G为轨道不平顺谱的特征参数，可根据轨道不平顺类型选取不同的参数值。

在利用上节的谱表示-随机函数方法模拟轨道不平顺时，需要将式(10)的空间域功率谱密度转换为时域功率谱密度。根据能量守恒原理，存在如下的关系

Sm(fm)dfm=St(ft)dft

(11a)

St(ωt)dωt=St(ft)dft

(11b)

于是，根据式(8)、式(10)及式(11)，得到轨道不平顺的时域功率谱密度

(12)

或

(13)

式中：St(ft)和St(ωt)都是时域功率谱密度，单位分别为mm2/Hz和mm2/(rad/s)；ft和ωt都是时间频率，单位分别为Hz和rad/s。

本文仅以轨道高低不平顺模拟为例，对于式(10)中的轨道不平顺功率谱密度，其左高低不平顺特征参数A～G的取值见文献[19]。考虑列车运行速度v=200 km/h、250 km/h、300 km/h三种工况，即v=55.56 m/s、69.44 m/s、83.33 m/s。由于在计算列车车体的有效加速度时，加权函数的频率范围为0.5～80 Hz，因此，空间波长取0.5～200 m。 于是，可计算下截止频率ω1=2πv/200， 上截止频率ωN=2πv/0.5，均能够包含加权函数的频率范围。

在模拟轨道不平顺随机过程时，首先需将基本随机变量Θ在区间(-π,π)上均匀离散化，本文建议的离散代表点计算公式为：

θi=-π+(i-0.5)π/72,i=1,2,3,…,144

(14)

式中：θi为离散代表点值， 代表点的数量nsel=144。

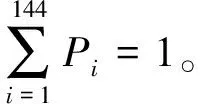
图1为谱表示-随机函数方法模拟得到的时域代表性样本曲线，从图中可知，生成的代表性样本具有轨道不平顺的平稳性特征。图2和图3分别为144条代表性样本集合的平均功率谱与目标功率谱在时域和空间域上的比较。可见，代表性样本集合的平均功率谱与目标功率谱具有很高的一致性，表明了本文方法模拟轨道不平顺的有效性。

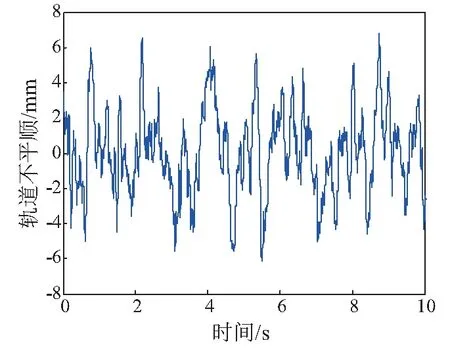
图1 轨道不平顺代表性样本Fig.1 Representative sample of track irregularity

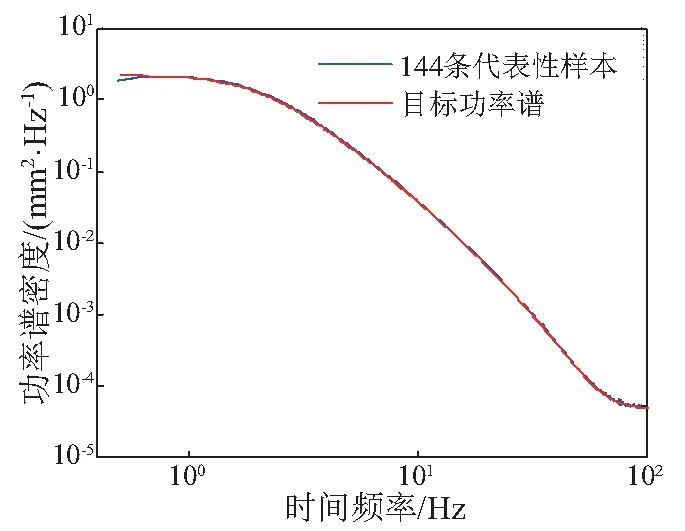
图2 样本功率谱与目标谱在时域的对比Fig.2 Comparison of power spectrum and target spectrum in time domain

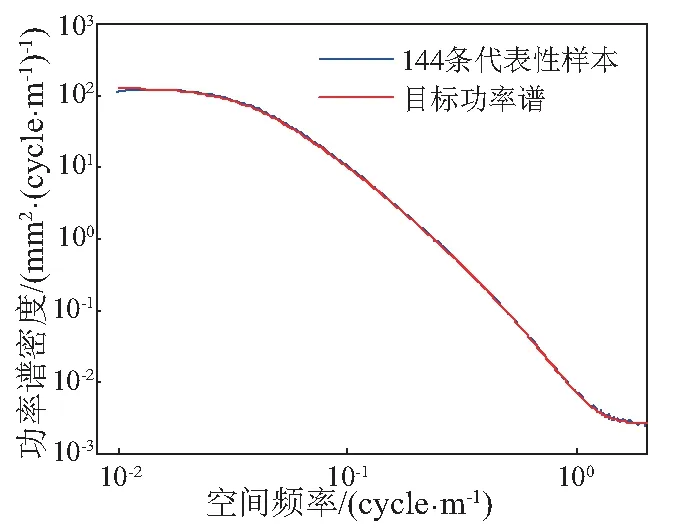
图3 样本功率谱与目标谱在空间域的对比Fig.3 Comparison of power spectrum and target spectrum in space domain

3 车辆-轨道耦合系统的概率密度演化方法

旅客乘车一般可分为站姿、坐姿和卧姿三种方式，不同乘车方式对于列车各个方向的振动敏感性不同，因而在研究乘坐舒适度时所考虑的侧重点也不同。由于旅客在乘坐高速列车时，主要以坐姿为主，坐姿的旅客对列车竖向振动加速度敏感性更为明显，轨道高低不平顺所引起的竖向加速度过大时，会引起更大的噪声危害，对旅客造成不舒适感。

为此，本文仅以轨道高低不平顺作为随机激励源，在利用谱表示-随机函数方法表达随机激励源时，其随机性完全来源于基本随机变量Θ， 且Θ为在区间(-π,π)上均匀分布。车辆-轨道耦合系统采用竖向振动模型[20]，耦合系统响应的求解，可利用有限元方法来实现。通过将耦合系统分解为上部车辆子系统和下部轨道子系统，采用Newmark-β数值积分方法对两子系统分别交叉迭代独立求解[21]。

对于车辆子系统，采用附有二系弹簧阻尼的整车模型，其动力方程为

Muau+Cuvu+Kuxu=Qug+Ful(Θ)

(15)

式中：Mu、Cu和Ku分别为车辆子系统的质量矩阵、阻尼矩阵和刚度矩阵；xu、vu和au分别为车辆子系统的位移、速度和加速度向量， 其中加速度向量au={ac,αc,at1,at2,α1,α2,aw1,aw2,aw3,aw4}T，ac和αc分别为车体的竖向加速度和角加速度，ati和αi(i=1,2)分别为转向架的竖向加速度和角加速度，awi(i=1,2,3,4)为车轮竖向加速度；Qug为车辆重力向量；Ful(Θ)为轮轨接触力向量。

对于轨道子系统，其动力方程为

Mlal+Clvl+Klxl=Qlg-Ful(Θ)

(16)

式中：Ml、Cl和Kl分别为轨道子系统的质量矩阵、阻尼矩阵和刚度矩阵；xl、vl和al分别为轨道子系统的位移、速度和加速度向量；Qlg为轨道结构重力向量。

在式(15)和式(16)中，车辆单元采用CRH3型高速列车，轨道单元分别采用我国干线60 kg/m有砟无缝线路和CRTS-Ⅱ型无砟轨道线路，其参数见文献[21]。

对于上述保守的车辆-轨道耦合随机动力系统，其解答是存在且唯一的，而且是基本随机变量Θ和时间t的函数。对于感兴趣的具体物理量，如车体竖向加速度ac(随机过程)，其解答可写为

ac=Z(Θ,t)

(17)

则车体竖向加速度ac的时间变化率为

(18)

由于耦合动力系统的随机性完全来源于基本随机变量Θ，因此，扩展的随机动力系统(Z,Θ)是一个概率保守系统。根据概率守恒原理的随机事件描述，可得广义概率密度演化方程为

(19)

于是，在给定的初始条件和边界条件下求解式(19)获得联合概率密度函数pZΘ(z,θ,t)之后， 即可得到车体竖向加速度Z的概率密度函数

(20)

式中：ΩΘ为Θ的分布空间。

在车辆-轨道耦合系统的概率密度演化数值分析中，基本步骤如下：

(1) 生成轨道不平顺随机过程的代表性样本集合。基本随机变量Θ在区间(-π,π)上进行均匀离散化，选取代表性点集{θi,i=1,2,…,144}， 并计算代表性点的赋得概率Pi。 利用谱表示-随机函数方法模拟生成轨道高低不平顺的代表性样本集合{η(θi,t),i=1,2,…,144}， 同时得到代表性样本的赋得概率Pi。

(2) 求解确定性的车辆-轨道耦合动力系统。对于给定的轨道高低不平顺代表性样本η(θi,t)，进行确定性的车辆子系统式(15)和轨道子系统式(16)的动力响应计算，其中轮轨接触力向量Ful(θi)是通过Hertz非线性公式来计算[21]

(21)

式中：G为接触挠度系数；ywk为第k个车轮位移；ylck和ηk分别为第k个轮轨接触处的钢轨位移和轨道不平顺值。

在Newmark-β数值积分中， 时间步长取为0.000 2 s，动力响应计算时长取为10 s，收敛精度取为1.0×10-7。

(3) 求解广义概率密度演化方程。采用有限差分方法求解广义概率密度演化方程式(19)，得到联合概率密度函数的数值解答。

(4) 累计求和。对式(20)累计求和得到车体竖向加速度的概率密度函数数值解答。

图4～图7为有砟轨道情况下列车运行速度为200 km/h时车体竖向加速度的概率信息。其中，图4为车体竖向加速度的均值与标准差；图5为典型时刻的概率密度函数；图6为概率密度演化曲面；图7为等概率密度线。由此可以看出，概率密度演化方法可对系统响应进行精细化分析得到丰富的概率信息，这为基于概率密度函数的、精细化的车辆-轨道随机动力响应分析奠定了基础。

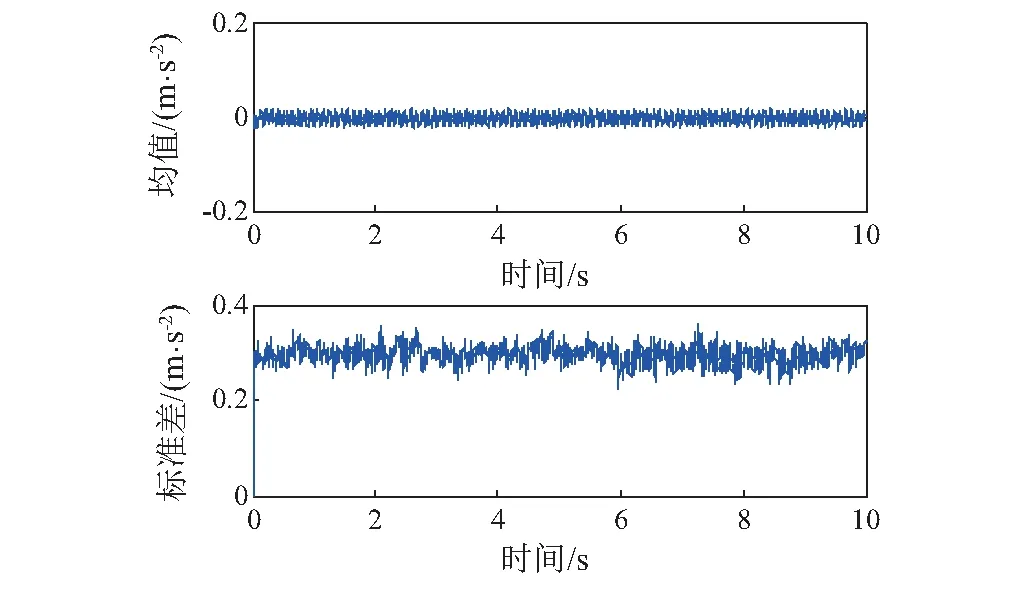
图4 均值与标准差Fig.4 The mean and the standard deviation

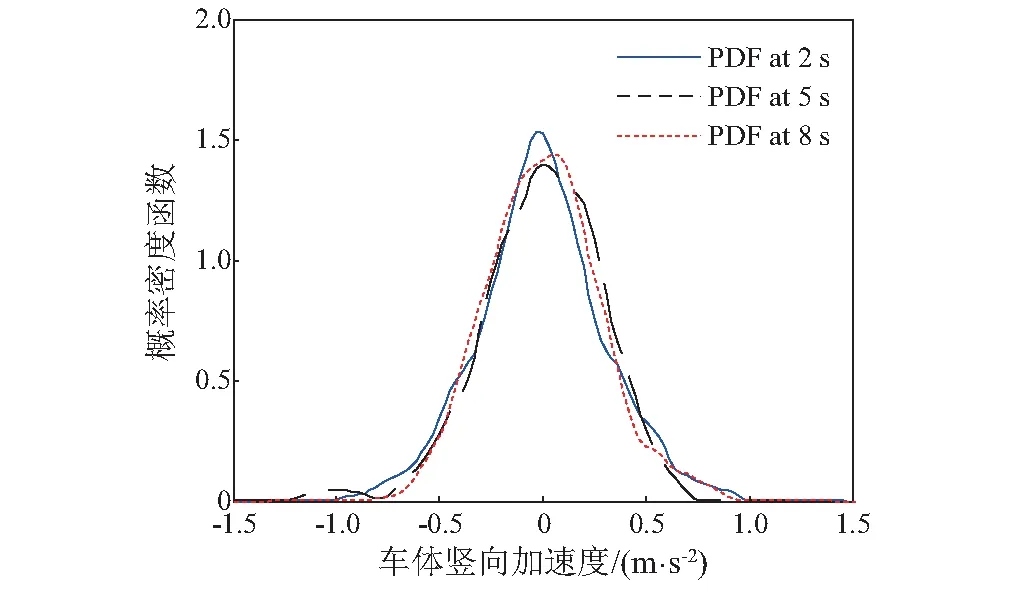
图5 典型时刻的概率密度函数Fig.5 Typical probability density function at certain time of instants

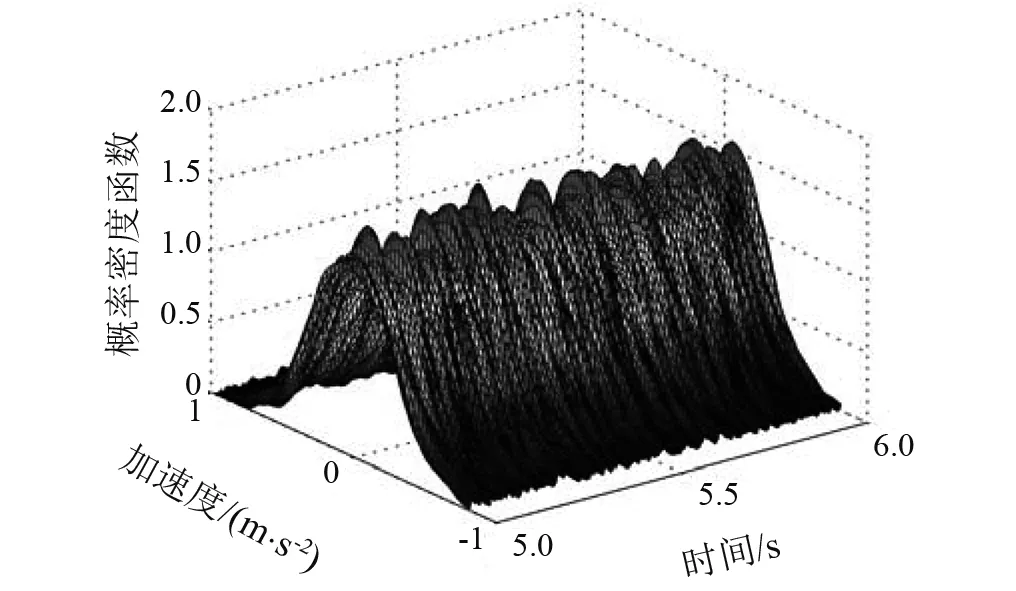
图6 概率密度演化曲面Fig.6 The probability density function surface

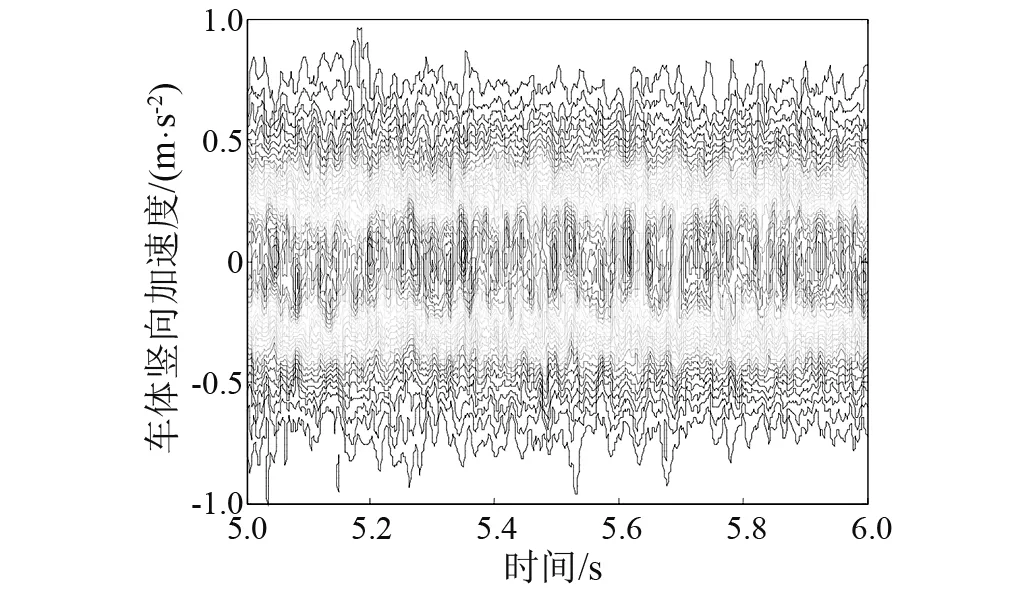
图7 等概率密度线Fig.7 The contour of the probability density function surface

4 舒适度评价的概率密度演化方法

4.1 评价标准

旅客乘坐舒适性是评价车辆运行品质的重要标准，一般分为舒适度评价和平稳性指标评价。其中，舒适度评价参考标准有ISO2631国际标准和UIC513标准；平稳性指标评价参考标准有Sperling标准和GB 5599—85标准。

本文采用UIC513标准的简化方法进行舒适度评价，其计算公式为[22]：

(22)

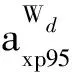
竖向有效加速度值可采用下式进行计算

(23)

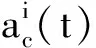
(24)

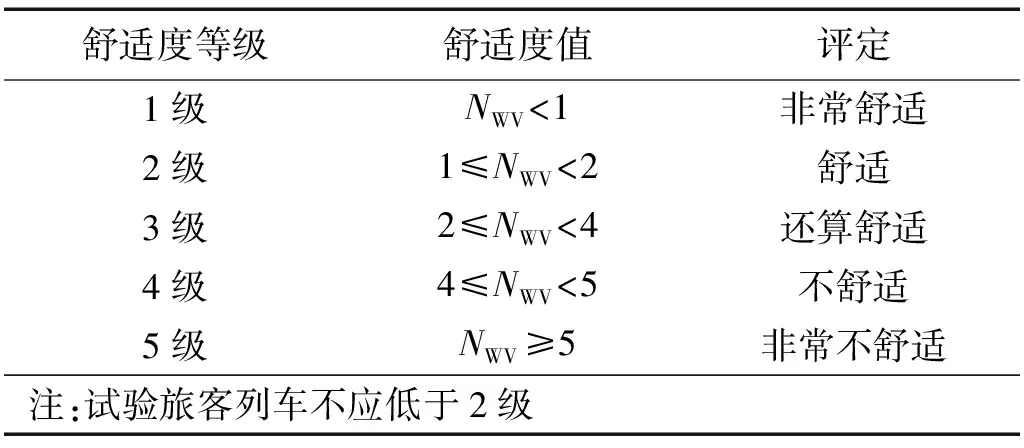
表1 UIC513舒适度等级划分

4.2 舒适度评价

应用概率密度演化方法，可以方便地计算有效加速度(随机变量)的概率密度函数和分布函数。当列车运行速度分别为200 km/h、250 km/h和300 km/h时，采用概率密度演化方法得到有效加速度的概率密度函数和分布函数，如图8和图9所示。对于有砟轨道线路，列车运行速度分别为200 km/h和250 km/h时，车体有效加速度的95%置信点值分别为0.226 m/s2和0.278 m/s2；对于无砟轨道线路，列车运行速度分别为200 km/h、250 km/h和300 km/h时，车体有效加速度的95%置信点值分别为0.223 m/s2、0.267 m/s2和0.307 m/s2。利用式(22)即可计算相应的舒适度值，对于有砟轨道线路，舒适度值分别为1.356和1.668，均属于2级舒适度；对于无砟轨道线路，舒适度值分别为1.338、1.602和1.842，也均属2级舒适度。这与文献[22]采用实测轨检数据得到的高速列车舒适度评价结果相一致。此外，CRTS-Ⅱ型无砟轨道线路的乘坐舒适度略优于我国干线60 kg/m有砟轨道线路，且随列车运行速度的提高，无砟轨道线路的优势逐渐增大。

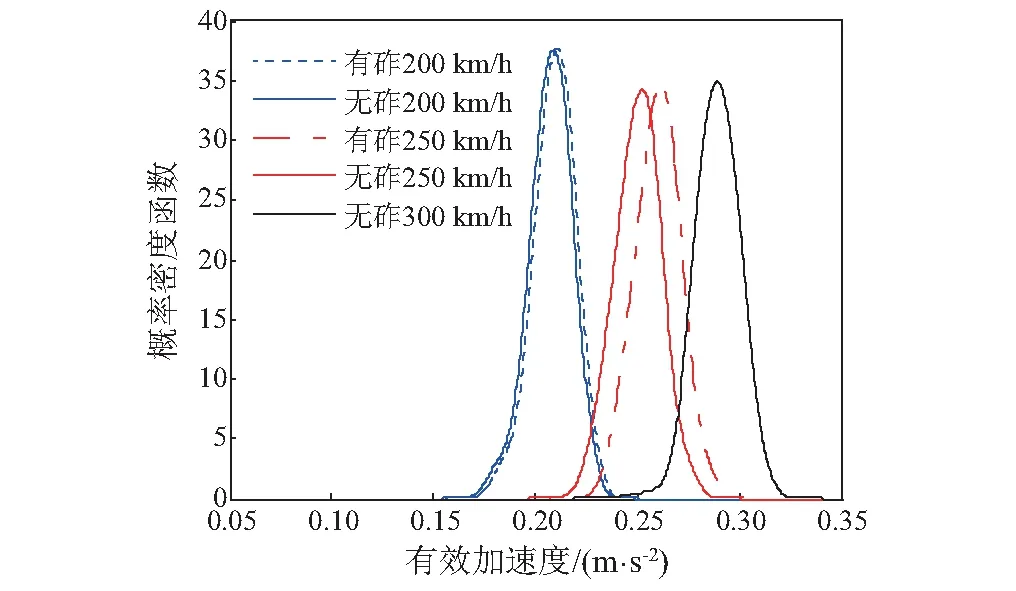
图8 有效加速度的概率密度函数Fig.8 Probability density function of effective acceleration

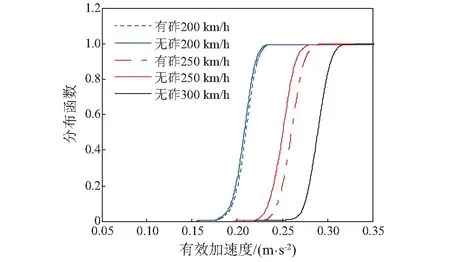
图9 有效加速度的分布函数Fig.9 Distribution function of effective acceleration

为进一步说明概率密度演化方法与直方图统计方法的差异，图10给出了有砟轨道线路下列车运行速度为200 km/h时，采用概率密度演化方法和直方图统计方法得到有效加速度的分布函数对比图。

从图10可知，直方图统计方法的分级间隔大小对有效加速度的分布函数影响较大，进而影响舒适度评价结果。采用概率密度演化方法则可得到精确的有效加速度分布函数，表明了本文方法的优越性。

图10 概率密度演化方法与统计方法对比Fig.10 Comparison of probability density evolution method and statistical method

5 结 论

本文采用平稳随机过程的谱表示-随机函数方法模拟了我国干线铁路轨道不平顺，并结合概率密度演化方法和UIC513舒适度评价标准，研究了高速列车在轨道不平顺随机激励作用下的车体竖向加速度和旅客乘坐舒适度。根据分析结果得出如下结论：

(1) 通过本文建议的谱表示-随机函数方法，可构造强约束的标准正交随机变量形式，只需一个基本随机变量即可精确模拟轨道不平顺随机过程，且模拟生成的代表性样本集合具有完备的概率集，这一特点使得其与概率密度演化方法具有天然一致性，可以方便地对随机振动响应进行分析。

(2) 概率密度演化方法可以获得任意时刻所需系统响应的瞬时概率密度函数及其演化过程，这为基于概率密度函数的、精细化的列车随机动力响应分析奠定了基础。

(3) 通过概率密度演化方法和直方图统计方法的比较，可见，概率密度演化方法对有效加速度进行处理可以获得精确的分布函数，提高了舒适度评价的精确性。