基于VMD滤波和极值点包络阶次的滚动轴承故障诊断

武英杰， 辛红伟， 王建国， 王晓龙

(1. 东北电力大学 自动化工程学院，吉林 132012； 2. 华北电力大学 能源动力与机械工程学院，河北 保定 071003)

滚动轴承广泛应用于旋转机械，其健康状态直接影响整个设备的安全、经济运行。实际中，一些旋转机械(例如变频电机、风机等)经常处于变速、变载运行工况，因此，变工况下的滚动轴承状态监测与故障诊断研究具有重要意义。

阶次分析是变速工况下旋转机械故障诊断的有效方法，其中参考转速可直接测量或估计[1]。康海英等[2-3]主要采用了计算阶比跟踪法(Computed Order Tracking，COT)，将时域信号转变为角度信号进行分析，研究变速过程中的旋转机械故障诊断。Borghesanin等[4]提出了RS-SES方法，即先求包络信号再角度域重采样，该方法较直接在时间域重采样具有更好的计算效率和有效性。在包络阶次分析中，重采样频率往往需要经验或凑试，为此，郝高岩等[5]提出了一种基于滤波定阶理论的阶次包络谱分析方法，通过对解调后信号低通滤波，确定计算阶次跟踪的重采样频率。Abboud等[6]以旋转机械振动信号建模仿真为基础，综合运用多种方法(平方包络谱、阶次跟踪、同步平均、倒谱预白化)对变速工况滚动轴承进行故障诊断。

本文针对变速工况振动信号非平稳特性、传统包络解调局限性[7]，提出了一种基于VMD滤波和极值点包络阶次的特征提取方法，并通过与基于Hilbert变换的包络阶次对比，说明本方法的特点及有效性，最后应用于滚动轴承故障诊断。

1 变分模态分解(VMD)滤波

1.1 VMD算法

VMD信号分解方法的整体框架是变分问题的求解，使得每个模态的估计带宽之和最小，其中假设每个‘模态’是具有不同中心频率的有限带宽，为解决这一变分问题，采用了交替方向乘子法，不断更新各模态及其中心频率，逐步将各模态解调到相应的基频带，最终各个模态及相应的中心频率被一同提取出来[8]。

该方法通过引入二次惩罚因子α和拉格朗日乘法算子λ(t)，将约束性变分问题变为非约束性变分问题，其中二次惩罚因子可在高斯噪声存在的情况下保证信号的重构精度，拉格朗日算子使得约束条件保持严格性，扩展的拉格朗日表达式为：

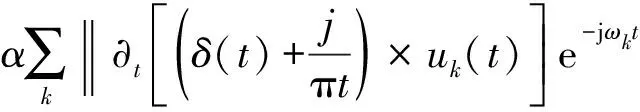
(1)

式中：f(t)为原信号;uk为各模态信号;ωk为各模态对应的中心频率; VMD具体实现算法如下：

(2) 更新uk和ωk：

(2)

(3)

(3) 更新λ：

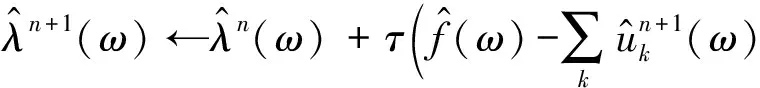
(4)

1.2 VMD滤波特性

设观察信号f0(t)由原信号f(t)和噪声η组成：

f0(t)=f(t)+η

(5)

若按照均方误差最小的准则：

(6)

(7)

式中：α为惩罚因子，其大小影响滤波的保真度。

实际信号分析发现，VMD具有类似小波包分解的特性[9]，这与VMD能够将不同频率段模态成分分离相一致。文献[10]研究显示，VMD在提取低频分量时，明显优于递归式模态分解方法(如EMD、LMD及EEMD等)，本文将VMD用于变速工况振动信号滤波。考虑到滚动轴承故障引起的共振频带往往在高频段，因此，VMD信号重构时，可剔除低频分量成分，以抑制转速升高、降低引起的振动幅值波动，同时利用VMD的维纳滤波特性，提高信噪比。

2 极值点包络阶次与仿真

2.1 极值点包络阶次

包络阶次主要分为求取包络信号和角度域重采样两部分，传统的包络信号求取有：平方包络法和Hilbert变换法等，本文采用了基于极值点的包络线法[11]，其中，借鉴EMD算法中的包络求取方法，利用振动数据极大值点，直接插值拟合其包络线，基于极值点的包络阶次流程如图1所示。

图1 基于极值点的包络阶次流程Fig.1 Extreme point based envelope order flow

(1) 确定极大值。寻找时域振动数据极大值，组成极大值数据序列。

(2) 对极大值序列的端点进行延拓。借鉴EMD中常用的端点处理方法(镜像法、波形匹配及数据预测法等[12])，本文采用简单有效的次端点镜像法对极大值序列端点进行延拓。

(3) 插值拟合。对端点延拓后的极大值序列进行三次样条插值拟合，从而得到包络线信号。

(4) 低通滤波。为了避免角度域重采样频率过大(增大计算量)或过小(阶次混叠)，本文采用郝高岩等的采样频率确定方法，对时域包络线信号进行截止频率可调的低通滤波处理。

(5) 计算阶比跟踪。结合转速脉冲信号，采用计算阶比跟踪技术实现包络线信号的角度域重采样。

(6) 对角度域包络线进行FFT，得到包络阶次谱。

2.2 极值点包络仿真

下面采用仿真信号说明基于极值点的包络阶次过程及其特性。首先，仿真一扫频调幅信号，幅值调制信号包含直流分量，即：

y(t)=(sin(2πf0t*1.8)+1)*sin(2πf0t*8.2)

(8)

式中： 采样频率为4 096 Hz，f0在1 s内从0 Hz线性增加至10 Hz，仿真信号如图2所示。采用基于极值点的方法画出包络线信号(虚线)，不难发现，y(t)的包络线即为调制信号。

若以x(t)=sin(2πf0t)为参考轴，仿真出相对应的转速脉冲信号，即每转一周，在键相处产生一个脉冲序列，仿真结果如图2所示，其中脉冲幅值为2。

图2 仿真信号及转速脉冲Fig.2 Simulation signal and corresponding speed pulse

相对于参考轴x(t)， 幅值调制信号对应的理论阶次为1.8，因此，无需通过低通滤波来确定角度域重采样频率。本文采用文献[13]的等角度时间序列计算和幅值拟合方法：选用二次曲线描述角度与时间的关系，选用三次样条插值拟合等角度采样后的幅值，其中，等角度采样间隔设为π/10。

基于极值点的时间域包络信号、角度域包络信号及阶次谱，如图3(a)所示，其中，调幅成分1.765阶次被成功解调出来；基于Hilbert变换的包络阶次谱求取过程如图3(b)所示，不难发现，两种方法得到的角度域包络信号在幅值和相位上完全一致，最终均可将调制阶次1.765解调出来。

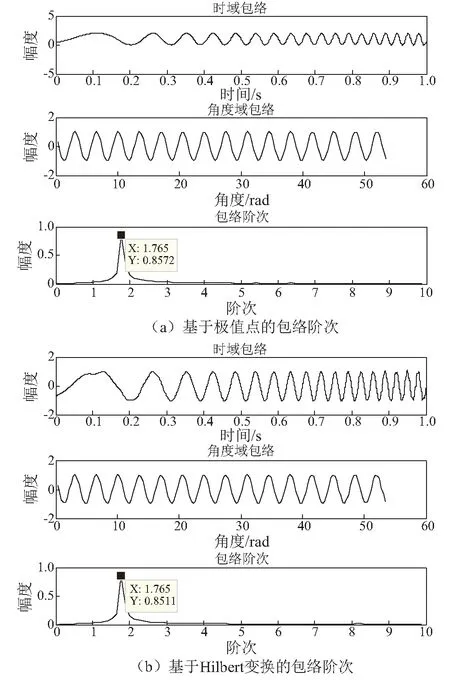
图3 扫频调幅信号的解调结果Fig.3 Demodulation results of chirp modulated signals

若将仿真信号y(t)调整为带有幅值调制的两个扫频信号之和，即

y(t)=x1(t)+x2(t)

(9)

x1(t)=(sin(2πf0t*1.8)+1)*sin(2πf0t*8.2)

(10)

x2(t)=sin(2πf0t*2.2+π/6)

(11)

图4为幅值解调结果，可以看出，对于本文的仿真信号，基于极值点的包络方法可以将调幅阶次1.765解调出，同时，也可将低频成分x2(t)对应的阶次成分(2.235阶)解调出，而基于Hilbert变换的包络方法在实现幅值解调的同时，将两个扫频信号阶次之差(8.2-2.2)解调出来，这与平稳信号的解调结果是一致的[7]。

多次仿真实验发现，当调制阶次大致小于载波阶次的1/2时，基于极值点的包络解调总能将低阶调制信号解调出，目前，这一结论尚难从理论上进行解释。

基于仿真实验分析，当处理实际变速工况故障信号时，可采用VMD分解将各“模态”分散开来，使得载波阶次尽量远离调制阶次，本文通过VMD滤波去除低频分量，抑制转速波动带来振动趋势变化。

图4 带幅值调制的扫频信号之和的解调结果Fig.4 Demodulation results of the sum of two chirp modulated signals

3 变速工况轴承故障诊断应用

3.1 滚动轴承故障实验

实验数据源于QPZZ-Ⅱ旋转机械振动及故障模拟实验平台，如图5所示，其传动系统由三相交流变频电机、皮带传动轮、传动轴、联轴器、轴承及旋转轴构成，其中，正常轴承位于旋转轴左侧，故障轴承位于旋转轴右侧，振动传感器位于故障轴承的垂直方向。实验中模拟了变速工况下滚动轴承故障(内圈、外圈、滚动体及复合故障)，发电机转速从低速增加到1 470 r/min，采用光电转速脉冲传感器测量转速，采用PCB352C65传感器拾取振动信号，其中，采样频率为12 800 Hz，故障轴承型号为6205深沟球轴承，故障特征阶次如表1所示。

正常状态下的时域信号及对应的转速信号(由转速脉冲信号得来)，如图6所示，根据转速信号可以看出，轴承转速经历了2次加速过程，而时域波形的振幅大体上经历了两次由小变大的过程，这是转速升高、降低、再次升高引起的，时域振动信号为大范围内的非平稳信号。

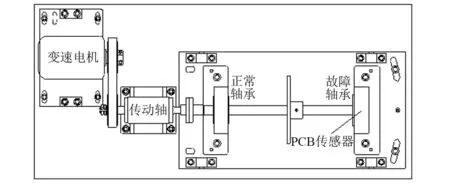
图5 变速实验平台示意图Fig.5 Schematic diagram of test platform for variable speed

轴承型号外圈故障阶次内圈故障阶次保持架故障阶次滚动体故障阶次6 2053.5855.4150.3984.714

图6 正常状态时域波形及转速信号Fig.6 Waveform of normal signal and speed signal

3.2 诊断应用

为验证本文方法的有效性，下面采用滚动轴承内圈、滚动体及复合故障进行分析，其中，时域振动信号均取3 s数据长度，以内圈故障信号为例进行VMD滤波，结果如图7所示。可见，滤波后信号更加“纤瘦”，冲击成分更为明显，而滤波前信号幅值带有明显的上升趋势，因此，基于VMD的滤波方法可提高信噪比，并有效抑制了转速变化引起幅值波动，以减小对后续故障特征提取的影响。

图7 VMD滤波Fig.7 VMD filtering

对内圈故障包络信号进行低通滤波，根据滤波定阶理论，包络信号的角度域重采样间隔设定为π/15，即角度域采样频率为30，由于内圈故障分析阶次较外圈、滚动体高，因此，以下角度域采样频率均为30。内圈故障角度域包络信号及阶次谱如8所示，其中，滤波前角度域信号(图8(a))有明显的上升趋势，进而导致包络阶次谱中出现了大幅值直流分量成分。图8(b)为VMD滤波后效果，可以看出，角度域包络中的趋势项受到显著抑制，包络阶次谱中的故障阶次5.351得以凸显。由于该方法在重采样前进行了低通滤波，因此，故障阶次(5.351)对应的左边频带幅值明显，图中实线箭头对应1、2、3、4阶次；虚线箭头对应故障阶次(5.351)的左边频带：1.351、3.351阶次。

采用滚动体故障数据进行分析，滤波前的角度域包络信号(图9(a))整体上具有一定波动性，阶次谱成分较为复杂，其中，4.691为故障特征阶次。滤波后(图9(b))包络信号波动性消失，故障特征阶次更加凸显。同样，采用内圈外圈复合故障进行分析，依然可以得到含有明显故障特征的包络阶次谱(图10)。

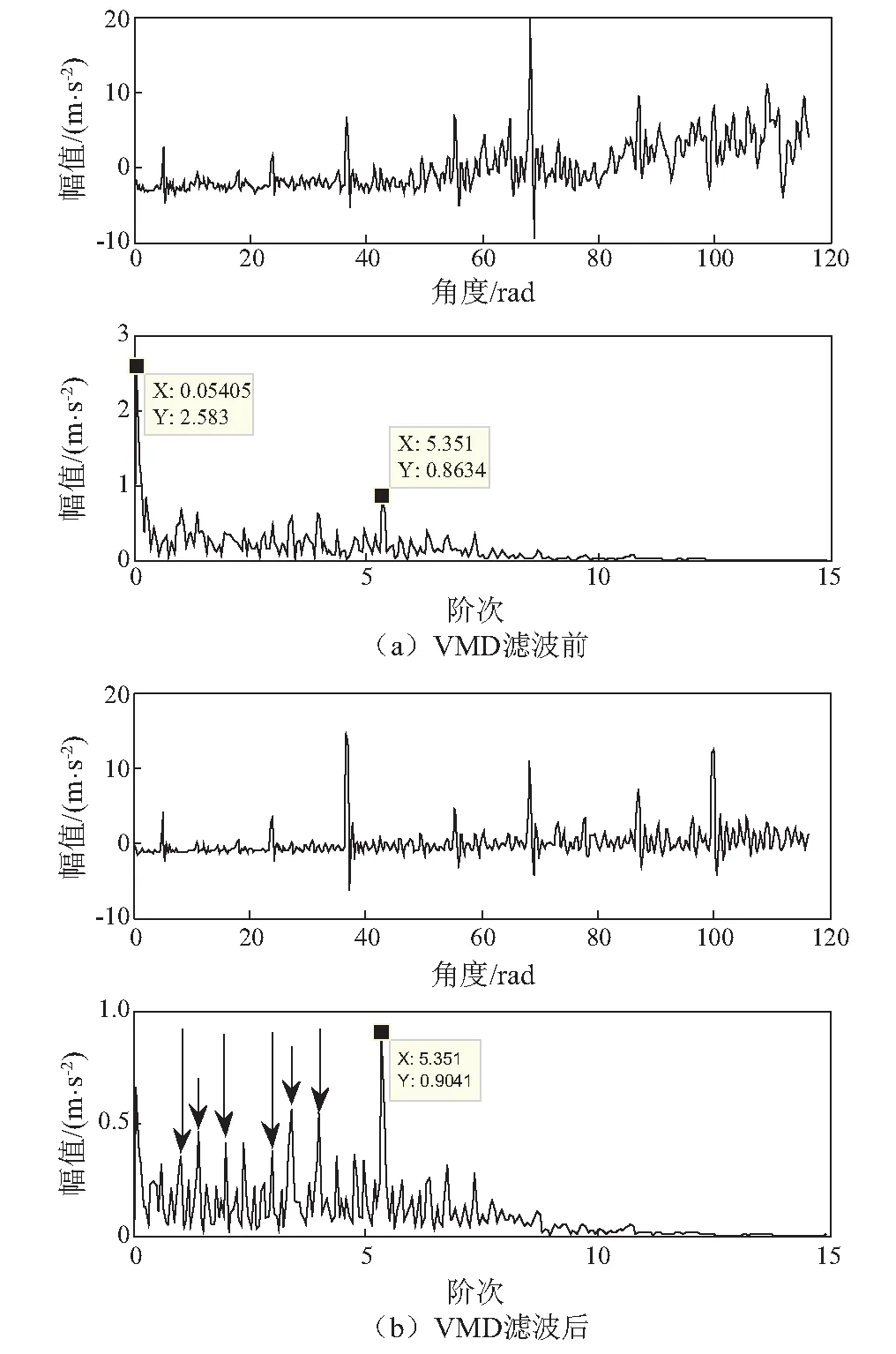
图8 内圈故障角度域信号及包络阶次谱Fig.8 Inner race failure signal in angle domain and corresponding envelope order spectrum

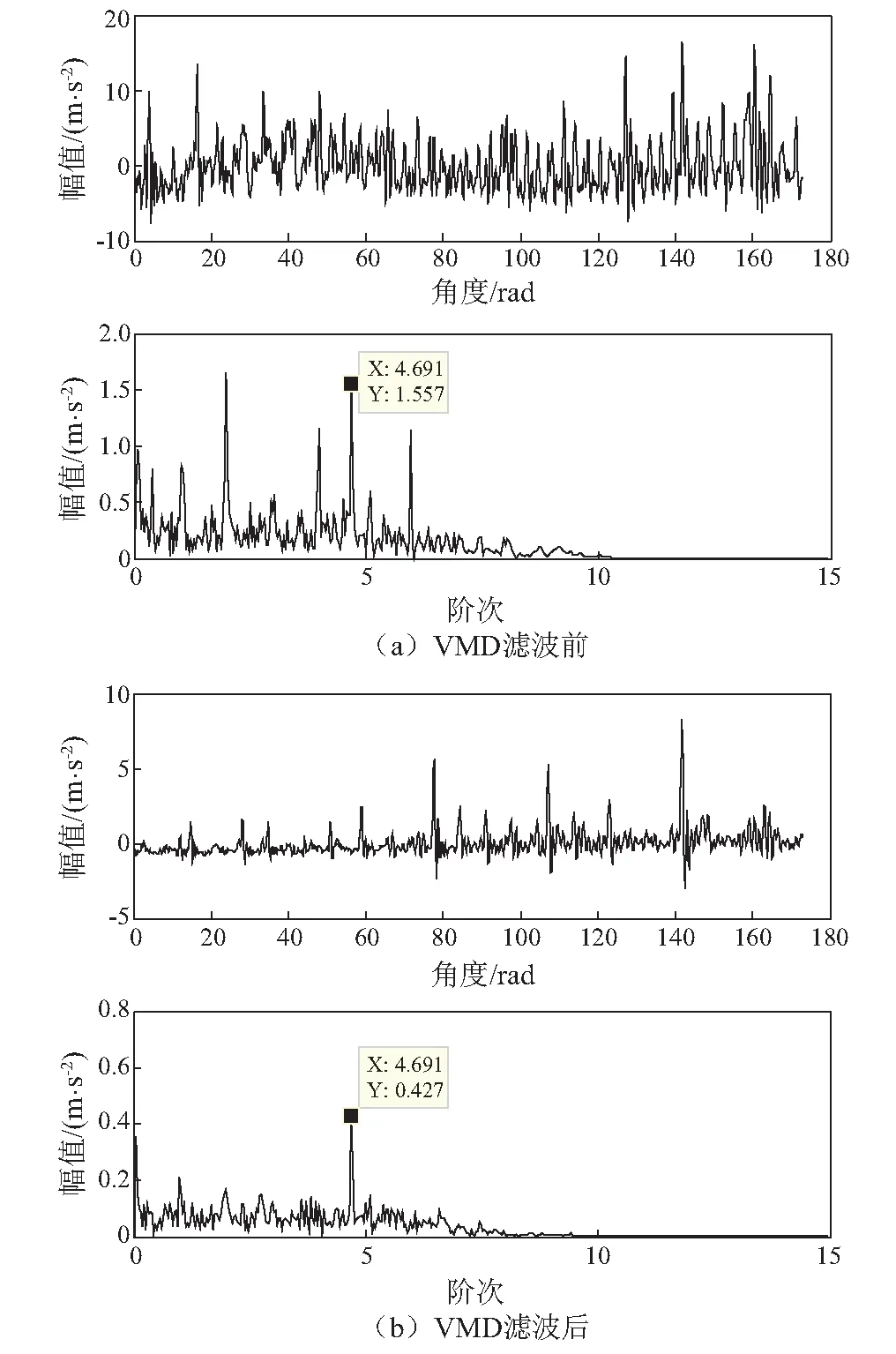
图9 滚动体故障角度域信号及包络阶次谱Fig.9 Ball element failure signal in angle domain and corresponding envelope order spectrum

图10 复合(内圈外圈)故障角度域信号及包络阶次谱Fig.10 complex failure signal in angle domain and corresponding envelope order spectrum

4 结 论

(1) 仿真分析表明：在一定条件下，基于极值点的包络法能够将混合扫频信号中的调制成分和低阶扫频信号解调出，这不同于将两扫频信号阶次之差解调出的Hilbert变换法。

(2) VMD滤波可明显抑制转速波动引起的振动趋势变化，且其本身的自适应维纳滤波特性，提高了信噪比，有利于变速工况下的滚动轴承故障诊断。

(3) 实验数据分析表明，基于VMD滤波和极值点包络阶次的特征提取方法可以实现滚动轴承单一及复合故障诊断，是一种有效的变速工况故障诊断方法。