动力学中临界条件的点线面

湖北 徐 进

牛顿运动定律是经典力学的擎天柱，是动力学的核心内容，高考考试大纲中对牛顿第一定律和牛顿第三定律的考查主要以知识的记忆和理解为主，而对牛顿第二定律的考查要求较高，属Ⅱ级要求，综合性较强，是高频考点，主要是对矢量性、瞬时性、同体性、独立性、相对性等的考查。牛顿第二定律在每年的高考中都会涉及，仅作为单一的知识点考查，统计分析如下(近几年全国卷)。

一、统计及其分析

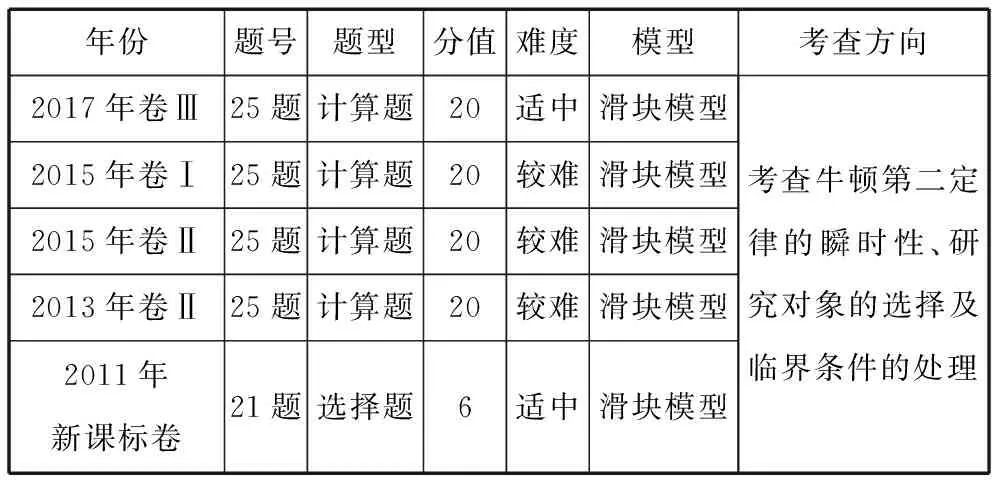
年份题号题型分值难度模型考查方向2017年卷Ⅲ25题计算题20适中滑块模型2015年卷Ⅰ25题计算题20较难滑块模型2015年卷Ⅱ25题计算题20较难滑块模型2013年卷Ⅱ25题计算题20较难滑块模型2011年新课标卷21题选择题6适中滑块模型考查牛顿第二定律的瞬时性、研究对象的选择及临界条件的处理

二、为什么这样考

1.此内容易错且难掌握，考查学生分析研究动力学的基本功，此内容属于易错知识；

2.体现牛顿第二定律的基本性质——矢量性、同一性、瞬时性、独立性；

3.体现确定研究对象的方法——整体法、隔离法；

4.突出考查“四翼”思想——基础性、应用性、综合性、创新性。

三、研究此类问题的基本思路

基本思维如下：

1.审题找关键字眼；

2.确定研究对象，分析运动过程；

3.找准瞬时关系；

4.抓住两过程的衔接点——临界条件;

5.发散思维、一题多变、举一反三。

下面从点、线、面全方位对动力学中的临界条件进行归纳总结，以飨读者。

四、临界条件归类

1.分离类临界条件

【例1】如图1所示，倾角为θ的光滑固定斜面上有一轻弹簧，下端与斜面底部连接，上端与物块A连接，B物块叠放在A上面，A、B物块的质量均为M，静止时弹簧被压缩了L，对B物块施加平行于斜面的力，下列判断正确的是

( )

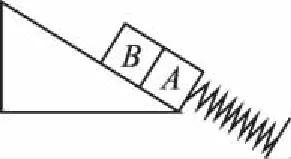
图1

A．若施加沿斜面向下的最大值为F1的变力，使弹簧缓慢压缩，要使撤去F1后的运动中A、B能分离，应满足F1>2Mgsinθ

B．若施加沿斜面向下的F2=2Mgsinθ的恒力，使弹簧再压缩L时立即撤去F2，以后的运动中A、B一定能够分离

C．若施加沿斜面向上的F3=Mgsinθ的恒力，到A、B两物块分离时沿斜面向上运动了大小为L的位移

D．若施加沿斜面向上的F4=2Mgsinθ的恒力，A、B两物块立即分离

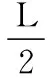
【答案】ABD

【点评】本题的关键是抓住分离瞬间的临界条件：加速度和速度相同，弹簧弹力为零。

【拓展一】若θ=90°，如图2所示，即系统变为竖直方向，其他条件都不变，则：

(1)施加向下的力缓慢压缩弹簧，要使A、B分离，则有F1>2Mg；

(2)施加向下的恒力F2=2Mg压缩L，则A、B将在弹簧原长处分离；

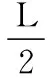
(4)施加向上的F4=2Mg的恒力，则A、B两物块立即分离。

图2

【拓展二】若θ=0，即系统处于水平方向，如图3所示，A、B带等量的正电荷q(不计A、B之间的作用力)，系统处在水平向左的匀强电场中，静止时弹簧压缩L，则：

(1)施加向左的力缓慢压缩弹簧，要使A、B分离，则有F1>2Eq；

(2)施加向左的恒力F2=2Eq压缩L，则A、B将在弹簧原长处分离；

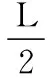
(4)施加向右的恒力F4=2Eq，则A、B两物块立即分离。

图3

【拓展三】如图4所示，A、B带等量的正电荷q(不计A、B之间的作用力)，处在沿斜面向下的匀强电场中，其他条件不变，则：

(1)施加沿斜面向下的力缓慢压缩弹簧，要使A、B分离，则有F1>2(Mgsinθ+Eq)；

(2)施加沿斜面向下F2=2(Mgsinθ+Eq)的恒力压缩弹簧L，则A、B将在弹簧原长处分离；

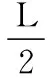
(4)施加沿斜面向上F4=2(Mgsinθ+Eq)的恒力，则A、B两物体立即分离。

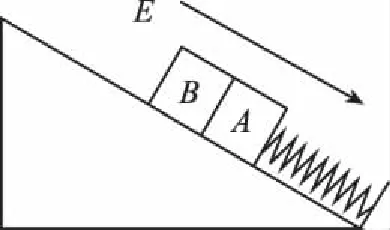
图4

2.滑块类临界条件

【例2】如图5甲所示,一质量为M的长木板静置于光滑水平面上,其上放置一质量为m的小滑块。木板受到水平拉力F作用时,用传感器测出长木板的加速度a与水平拉力F的关系如图5乙所示,重力加速度g=10 m/s2,下列说法正确的是

( )

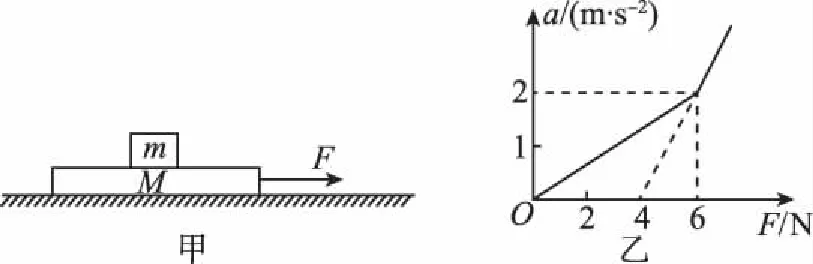
图5

A.小滑块的质量m=2 kg

B.小滑块与长木板之间的动摩擦因数为0.1

C.当水平拉力F=7 N时,长木板的加速度大小为 3 m/s2

D.当水平拉力F增大时，小滑块的加速度一定增大

【分析】当拉力较小时，m和M保持相对静止，一起做匀加速直线运动，当拉力达到一定值时，m和M发生相对滑动，可结合牛顿第二定律，运用整体法和隔离法进行分析。

【答案】AC

【点评】本题属于对下方的木板施加作用力的类型，解题的关键点是能用整体法求出系统最大的共同加速度。

【拓展一】如图6所示,地面依次排放两块完全相同的木板A、B,长度均为L=2.5 m,质量均为m2=150 kg,现有一小滑块以速度v0=6 m/s冲上木板A左端,已知小滑块质量m1=200 kg,小滑块与木板间的动摩擦因数为μ1,木板与地面间的动摩擦因数μ2=0.2。(最大静摩擦力与滑动摩擦力大小相等,取g=10 m/s2)

图6

(1)若小滑块滑上木板A时,木板不动,而滑上木板B时,木板B开始滑动,求μ1应满足的条件。

(2)若μ1=0.4,求小滑块运动时间。(结果用分数表示)

【解析】(1)滑上木板A时,木板不动,由受力分析得

μ1m1g≤μ2(m1+2m2)g

若滑上木板B时,木板B开始滑动,由受力分析得

μ1m1g>μ2(m1+m2)g

代入数据得0.35<μ≤0.5。

(2)若μ1=0.4,则小滑块在木板A上滑动时,木板不动。设小滑块在木板A上做减速运动时的加速度大小为a1,由牛顿第二定律得μ1m1g=m1a1

解得a1=4 m/s2

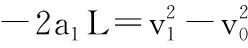
解得小滑块到达B板时速度v1=4 m/s

在A板上滑动时间由v1=v0-a1t1

解得t1=0.5 s

小滑块滑上B板时B运动,对B板用牛顿第二定律得

μ1m1g-μ2(m1+m2)g=m2a2

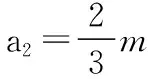
当小滑块和B板速度相同时有a2t2=v1-a1t2

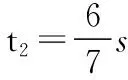
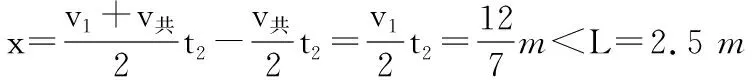
然后相对静止一起减速，有

μ2(m1+m2)g= (m1+m2)a共

【点评】此题中的滑块初始状态不同，过程很复杂，但只要牢牢抓住过程细节的衔接点，能把握不同状态下的受力情况和运动情况问题就可迎刃而解。

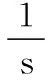
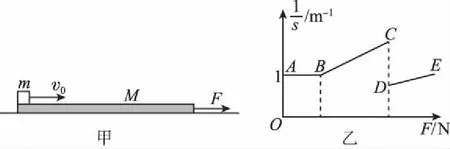
图7

(1)若恒力F=0，则物块会从木板的右端滑下，求物块在木板上滑行的时间t是多少；

(2)若恒力F=2 N，则物块与木板因摩擦而产生的热量Q为多少；

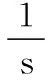
【解析】(1)以初速度v0为正方向,物块的加速度大小为am=μg=2 m/s2，木板的加速度大小为

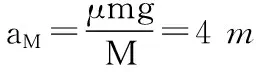
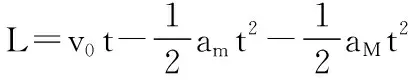
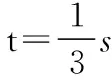
(2)①当F较小时,物块将从木板右端滑下,当F增大到某一值时物块恰好到达木板的右端,且两者具有共同速度v,历时t1，则有F+μmg=Ma1

根据运动学关系可得v=v0-amt1=a1t1

由图乙知，相对路程s≤1 m

代入解得F≥1 N。

②当F继续增大时,物块减速、木板加速,物块在木板上某一位置时二者具有共同速度;当二者共速后能保持相对静止(静摩擦力作用)，且以相同加速度a做匀加速运动，则有

F=(M+m)a，而f=ma

由于静摩擦力存在最大值,所以f≤fmax=μmg=2 N

联立解得F≤3 N

当F=2 N时有s=0.8 m

故有Q=μmgs=0.2×1×10×0.8 J=1.6 J。

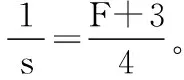
【点评】此题中滑块有初速度且木板受力，过程复杂，难度很大，解此类题的关键在于分析出两者具有相同速度时加速度及二者位移的关系。

3.连接体类临界条件

【例3】如图8所示,质量分别为m1、m2的A、B两个物体放在斜面上,中间用一个轻杆相连,A、B与斜面间的动摩擦因数分别为μ1、μ2,它们在斜面上加速下滑,关于杆的受力情况。下列分析正确的是

( )

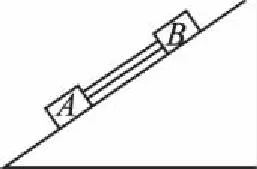
图8

A.若μ1>μ2,m1=m2，则杆受到压力

B.若μ1=μ2,m1>m2，则杆受到拉力

C.若μ1<μ2,m1

D.若μ1=μ2,m1≠m2，则杆无作用力

【解析】假设杆无弹力，物体A受重力、支持力和滑动摩擦力，根据牛顿第二定律，有m1gsinθ-μ1m1gcosθ=m1a1，解得a1=g(sinθ-μ1cosθ)，同理a2=g(sinθ-μ2cosθ)。若μ1>μ2,则a1a2，A加速度较大，则杆受到拉力，故C正确。

【答案】ACD

【点评】本题中用轻杆替代传统绳，假设杆无弹力，根据牛顿第二定律分别求解出A和B的加速度，比较大小，然后判断A、B的相对运动趋势，最后判断A、B间弹力的方向。

【拓展一】如图9所示，三个物体质量分别为m1=1.0 kg、m2=2.0 kg、m3=3.0 kg，已知斜面上表面光滑，斜面倾角θ=30°，m1和m2之间的动摩擦因数μ=0.8。不计绳和滑轮的质量和摩擦。初始用外力使整个系统静止，当撤出外力时，m2将(g=10 m/s2，最大静摩擦力等于滑动摩擦力)

( )

图9 图10

A.和m1一起沿斜面下滑

B.和m1一起沿斜面上滑

C.相对于m1下滑

D.相对于m1上滑

【答案】C

【点评】本题中将连接体通过滑轮放在斜面上，先后用假设法和整体法求出二者相对静止整体加速度，再用隔离法求出二者间的摩擦力，最后判断该摩擦力是否超过最大静摩擦力，从而判断能否保持相对静止。

【拓展二】如图11所示，有1、2、3三个质量均为m=1 kg的物体，物体2为一长板，与物体3通过不可伸长的轻绳连接，跨过光滑的定滑轮，设长板2到定滑轮足够远，物体3离地面高H=5.75 m，物体1与木板2之间的动摩擦因数μ=0.2。长板2在光滑的桌面上从静止开始释放，同时物体1(视为质点)在长板2的左端以v=4 m/s的初速度开始运动，运动过程中恰好没有从长板2的右端掉下，求：

(1)长板2开始运动时的加速度大小；

(2)长板2的长度L0；

(3)当物体3落地时，物体1在长板2上的位置。

图11

【解析】(1)隔离物体1，由牛顿第二定律有ma1=μmg

解得a1=2 m/s2

隔离长板2和物体3系统，由牛顿第二定律有

2ma2=mg+μmg

解得a2=6 m/s2。

(2)设经过时间t1二者的速度相等，有

v1=v-a1t1=a2t1

解得t1=0.5 s,v1=3 m/s

长板2的长度为L0=x1-x2=1 m。

则对物体1有ma=3.3 N>Ffm=μmg=2 N,故假设不成立，物体1和长板2仍相对滑动，有

物体1的加速度a3=μg=2 m/s2

整体下落高度h=H-x2=5 m

Δx=h-x3=1 m,即物体1在长板2的最左端。

【点评】此题在传统连接体的基础上加入另一个物体，题目过程略复杂，解答此题的关键是抓住关键字眼，理解速度和位移的几何关系，再利用假设法、整体法、隔离法求解。