基于三维形貌的错动节理非线性渗流特性研究

侯 迪，李莎莎，向国兴，熊 杰，杨 洁

(1.贵州省水利水电勘测设计研究院， 贵阳 550002；2. 贵州省喀斯特地区水资源开发利用工程技术研究中心，贵阳 550002；3. 武汉大学水资源与水电工程科学国家重点实验室，武汉 430072 )

0 引 言

在地质工程的建设中普遍存在岩石节理的渗透特性问题，如岩体洞室开挖、坝基处理等(Chen et al. 2008[1]， Mandal et al. 2011[2]，Wu et al. 2011[3]， Min et al. 2009[4]， Shen et al. 2010[5]，Barton and de Quadros 1997[6])。因此，岩石节理中渗透特性研究是近年来的一个研究热点。在早期的研究中，岩石节理被简化为光滑平面进行研究，建立了立方定律。Lomize(1951)[7]通过采用玻璃板模拟节理面实验验证了立方定理。然而，理解粗糙节理中渗流特性才是理解裂隙网络中渗流及溶质迁移的开始。在节理渗流的研究中发现，随着流速的增大流态会偏离线性规律而表现出非线性的现象。Zimmerman & Bodvarsson(1996)[8]通过分析Navier-Stokes方程，认为节理中非线性渗流的临街雷诺数为25。而大量实验研究表明当雷诺数大于1时，非线性渗流现象就会开始出现(Zimmerman et al.(2004)[9], Qian et al.(2005,2011)[10-11])。Ranjith& Darlington(2007)[12]展开了大量室内实验并得出结论认为界定线性流到非线性流转变的临界雷诺数应为10。Zhang & Nemcik(2013)[13]分别针对岩石吻合节理及岩石错动节理进行了室内实验，研究结果发现在岩石吻合节理中水压与流速呈线性规律，而错动节理中的流速随着水压的增大呈非线性规律。Forchheimer(1901)[14]和Izbash(1931)[15]针对岩石节理中的非线性渗流规律提出了经验模型进行描述。此外，Lee et al.(2014)[16]通过研究节理内的流速分布发现在雷诺数大于1的时候，立方定律不再适用。

由于立方定律无法体现节理粗糙度对渗流规律的影响，许多学者对立方定律进行了修正。Lomize(1951)[7]在大量实验的基础上对立方定律进行了修正，引入了一个能够表征节理面几何特征的修正系数λ。在此基础上，Witherspoon et al. (1980)[17]进一步研究发现修正系数λ的值在1.04～1.65之间。Cook et al.(1990)[18]、Zimmerman et al. (1992)[19]、Li et al. (2008)[20]等考虑节理面接触面积的影响对λ进行了进一步的修改。此外，速宝玉(1995)[21]讨论了相对粗糙度对节理渗透规律的影响。许光祥(2003)[22]研究了粗糙裂隙中渗流的超立方和次立方定律。Raven & Gale(1985)[23]研究了试样尺寸和加卸载次数对节理中非线性渗流规律的影响。耿克勤(1994)[24]、Olsson & Barton(2001)[25]通过实验定量研究了开度与流量之间的关系。

综上所述，国内外学者针对岩石节理渗透特性做了大量的工作。然而，已有的研究成果大多是基于节理剖面线的二维形貌参数进行研究，无法考虑岩石节理的尺寸效应、各向异性特征等。Hong et al. (2008)[26]指出二维形貌参数会在一定程度上低估岩石节理的粗糙程度。因此，采用真实岩石节理，考虑水压、法向荷载，采用三维形貌表征方法的岩石节理渗流实验有重要的研究价值。本文通过展开不同粗糙度错动节理中的渗流实验，分析了水压、荷载压力、岩石节理形貌与渗流量的关系；在此基础上提出了一个基于三维形貌参数的经验模型。提升了对岩石节理中非线性渗流特性的认识。

1 三维形貌表征方法

Grasselli et al. (2002)[27]提出了节理面有效剪切倾角的概念，并以此作为节理三维形貌表征参数。将节理面网格化如图1。计算公式如下:

tanθ*=tanθ(-cosα)

(1)

(2)

(3)

式中：m为θ*大于零的计算单元数；α为计算单元沿渗流方向的方位角；θ*为节理单元沿渗流方向与水平面的夹角；θ为计算单元与水平面的夹角；t为节理中渗流方向矢量；n0为水平面外法线矢量；n为节理单元外法线矢量；n1为n在水平面的投影矢量。

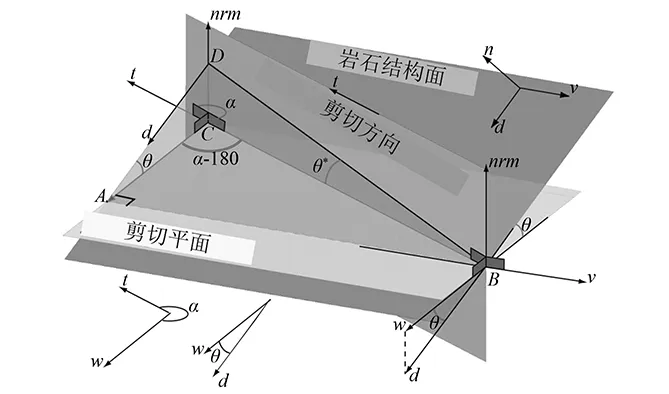
图1 视倾角计算示意图Fig.1 Identification of the apparent dip angle of triangular element.

(4)

式中：A0为面向岩石节理渗流方向的计算单元面积占岩石节理面所有计算单元表面积的比值。

(5)

将上式除以A0得到有效剪切倾角加权平均值θavg，如下式：

(6)

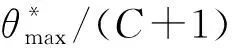
(7)

(8)

2 实验方法及实验结果

2.1 岩石节理试样制备

选取具有明显颗粒粗细差异的岩石试样制备成尺寸为200 mm×100 mm×100 mm的岩石节理劈裂试件，本文采用的岩石种类为花岗岩。标记为S1-FG、S2-MG 以及S3-CG。S1-FG代表细颗粒岩石节理试样其节理粗糙度较低、S2-MG代表中等颗粒岩石节理试样、S3-CG代表粗颗粒岩石节理试样其粗糙度较高。劈裂过程中荷载采用位移控制，其加载速率为0.5 mm/min，以确保得到的岩石节理表面相对比较光滑(见图2)。节理试样单轴抗压强度、泊松比等参数见表1，其中R2为计算粗糙度参数的拟合优度值。

图2 劈裂节理试样Fig.2 Split samples of granite with different grain size for samples

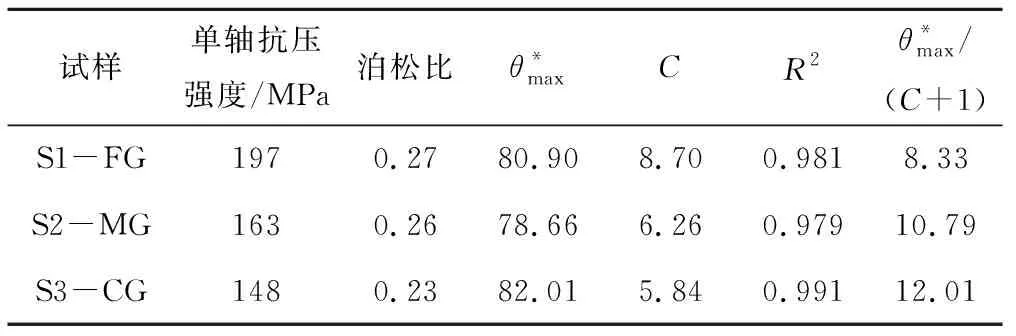
表1 节理试样参数Tab.1 Geo-mechanical and geometrical details of the fracture samples

2.2 试验过程

试验前先对岩石节理面进行扫描(图3)，计算岩石试样节理形貌参数，取点间距0.2 mm。然后展开岩石节理渗流实验，实验设备如图4。实验试样人工处理为饱和状态，错动1 mm后进行岩石节理渗流实验。渗流实验采用常法向荷载控制，实验中花岗岩岩石节理施加五级荷载为1.0～5.0 MPa，水压由进水口的水泵进行施加，实验中水压差采用0.1～0.8 MPa。将水压差除以试样长度200 mm，得到渗流实验的水力梯度为0.5、1.0、2.0、3.0、4.0 MPa/m。实验设备采集到的实验数据自动记录在计算机中。

图3 KEYENCE_LK-G5000扫描系统Fig.3 The 3D morphology scanner system

1-主机；2-加载系统；3-加载系统；4-变形测量仪；5-变形测量仪；6-试样固定仪；7-加载控制器；8-加载控制器；9-钢架；10-水泵；11-流量采集仪；12-垫块图4 水力耦合实验仪示意图Fig. 4 Schematic diagram of coupled shear-flow test system

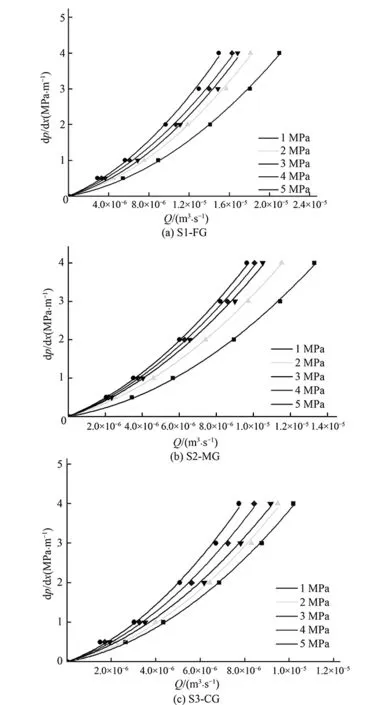
图5 水流流速与水力梯度关系图Fig.5 Regression analysis of pressure gradient as a function of measured flow rate using Forchheimer equation for samples

2.3 实验结果及分析

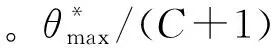
-▽p=aQ+bQ2

(9)

式中：a,b为常数；Q为岩石节理中的水流流速。

计算结果见表2。由表2可知，拟合参数数值会随着法相荷载的增大而增大，其增大趋势见图6。由图6可知，当法向荷载增大到一定数值时，拟合参数的数值几乎不再增加。拟合参数a为节理中渗流线性项常数，其随着法向荷载增大而增大，说明在法向荷载增大时，公式(9)中线性项aQ中的流速会减小，这是由于法向荷载的增大导致了开度的变小引起的。拟合参数b为节理中渗流非线性项常数，其随着渗透率的减小而增大，说明在渗透率减小时，公式(9)中非线性项bQ2所占的比例增大。此外，由表2中的计算结果可知，随着节理越粗糙度的增大，拟合参数a、b的值越大。这说明，随着节理粗糙度的增大，公式(9)中线性项aQ、非线性项bQ2中的流速都会减小。这是由于节理越粗糙，节理中的水流会更容易形成涡流，涡流会导致能量的损失，导致流量减小。

表2 渗流实验参数汇总表Tab.2 Summary of parameters for flow in non-mated rock fractures

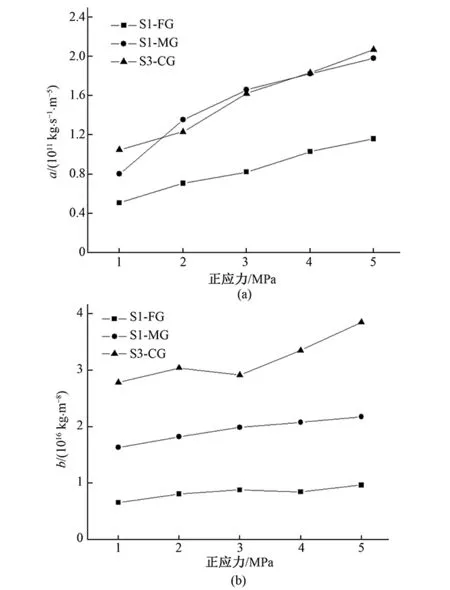
图6 法向荷载与拟合参数a、b之间的关系Fig.6 Variation of coefficients a and b with normal stress

由上文可知，在岩石节理非线性渗流特性的研究中，国内外学者常采用雷诺数常作为界定渗流线性与非线性的指标参数，计算方法如下：

(10)

式中：ρ为岩石节理中水的密度；e为岩石节理开度。公式(10)也可以变换成：

(11)

式中：w为岩石节理的宽度。

采用表观渗透率反应节理中的渗透特性，其计算方法如下：

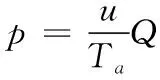
(12)

由公式(12)可知，若在吻合较好的岩石节理中，渗流基本呈线性趋势，此时公式(10)退化为达西定律，即Ta为达西定律中的渗透率。根据计算得到的表观渗透率值与雷诺数值得到图7。如图所示，表观渗透率会随着雷诺数的变化而改变，而在线性流中，渗透率为一个常数，不会随着雷诺数的改变而改变，说明在错动节理中存在这非线性渗流现象。且通过变化趋势，可知岩石节理中表观渗透率值越小，岩石节理中渗流的非线性作用就会越明显。

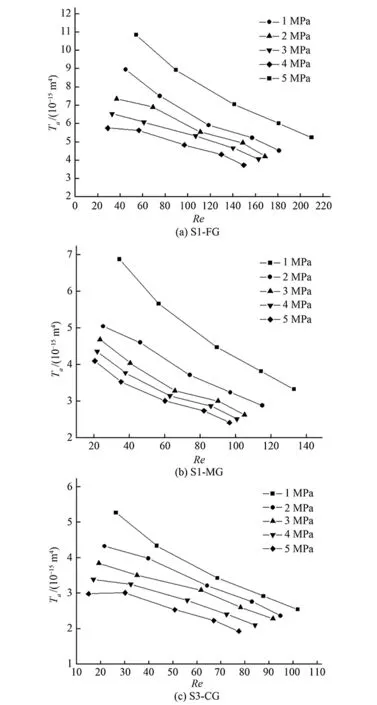
图7 渗透率与临界雷诺数关系图Fig.7 Apparent transmissivity versus Reynolds number for samples

在众多目前的研究中，常用非线性渗流项所占比例来界定线性与非线性流，计算方法如下：

(13)

工程应用中，常认为当这个比例小于10%时可以假定岩石节理中的水流属于线性流，其非线性的部分可以被忽略。

将α代入到雷诺数计算公式可以得到临界雷诺数的计算公式：

(14)

考虑α=0.1，得到：

(15)

通过计算可以得到实验中3组岩石节理在不同法向荷载及不同水压下的临界雷诺数值，见表2。由表2可知，临界雷诺数与法向荷载与节理粗糙度及施加的法相荷载之间存在函数关系。

由此，可以根据之前的假定计算节理的平均开度。选择雷诺数值小于临界雷诺数的工况，计算方法如下：

(16)

式中：J为渗流压差；e为需要求得的平均开度。

3 错动节理渗流模型

众多国内外学者考虑节理粗糙度的影响进行了立方定律的修正。如Lomiz 模型，在层流条件下，模型如下：

(17)

其中，λ=1+6.0(ε/e)1.5

式中：ε是节理相对粗糙度；e是水力开度。在紊流条件下，模型如下：

(18)

Louis (1969)[29]也提出了一种修正公式，计算如下：

(19)

其中，λ=1+8.8(ε/2e)1.5。

此外，Amadei[30]根据试验结果认为λ=1+0.6(ε/e)1.2。

然而，上述研究都是针对岩石节理相对粗糙度展开的，其在表征岩石节理真实三维形貌上存在不足。此外，上述研究中的室内实验大多是在严格的层流条件或者紊流条件下展开的，与真实节理中的渗流流态不符。

因此，本文提出了一种考虑节理三维形貌特征的经验模型。由实验结果可知，节理中渗流流速会随着节理粗糙度的增大而减小。由于涡流的影响，节理中平均水力开度会随着粗糙度的增大而减小。此外，流速会随着平均开度和水压的增大而增大。

由此，岩石节理中流速与节理开度之间的关系可用下式表示为：

(20)

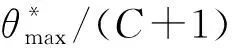
(21)

分析可知，上式与Izbash模型形式上相似。在工程实际中，当开度与粗糙度的取值不变时，上式流量与水力梯度存在函数关系，可以简化为Izbash模型。采用平均方差计算模型精度，公式如下：

(22)

计算得到其平均方差值为0.61%。说明其计算精度较高。

4 对渗流模型的对比讨论

为了验证公式(21)的合理性，本节将其与Forchheimer公式、Lomize模型以及Izbash经验模型进行对比分析。

Izbash经验模型如下：

-▽p=mQn

(23)

详细对比如下：

(1)在使用参数上，公式(21)采用三维相貌参数， Lomize模型是基于二维相貌参数相对粗糙度，而Forchheimer模型以及Izbash模型没有考虑节理相貌对渗流特性的影响。

(2)在模型形式上，公式(21)与Izbash模型在形式上一致，可以看作是Izbash模型在三维尺度上的扩展。两者皆为基于室内实验的经验模型。更适用于高水头作用下岩石节理中的非线性渗流规律。Forchheimer模型物理意义更明确，并得到了理论证明。

(3)在流态区分上，公式(21)与Izbash模型、Forchheimer模型都没有严格的层流紊流的划分。而Lomize模型对节理中渗流进行了层流和紊流的严格划分。而事实上，在工程实际中岩石节理中的渗流无法进行严格的层流与紊流的划分。

5 结 语

本文通过室内实验手段，进行了错动节理中的渗透实验研究，分析了节理中的非线性渗透规律，讨论了临界雷诺数及Forchheimer方程，并提出了错动节理中的非线性渗流公式。主要的结论如下。

(1)法向荷载、水压及形貌特征共同影响岩石错动节理中的渗流特性。在岩石错动节理中随着水压的增大，水压与流速之间逐渐偏离线性规律而呈现非线性现象。在错动节理渗流中，表观渗透率不是一个常数，并且随着雷诺数的增大而减小。

(2)定量分析了节理渗流中的线性项参数与非线性项参数，两个参数均与法向荷载存在函数关系，当法向荷载达到一定数值时，变化不再明显。

(3)随着节理粗糙度的增大，线性项参数与非线性项参数的值变小。说明，在越是粗糙的岩石节理中，水流越容易出现涡流现象，导致节理中的渗流量变小。

(4)提出了一种考虑节理三维形貌特征的经验模型，考虑了三维形貌参数，可以看做是对Izbash经验模型的一种扩展，形式上简单，具有重要的工程价值。