基于神经网络的信道译码算法研究综述

王玉环，尹航，杨占昕

(中国传媒大学广播电视数字化教育部工程研究中心，北京 100024)

1 引言

当今时代，神经网络技术得到了质的飞跃，应用范围也涉及到了多个领域。神经网络处理信息的规则和人脑的信息处理机制相似，具有并行运算、分布式存储、联想记忆、自组织自适应和容错的能力。

神经网络与纠错码技术有着相似的理论背景，尤其是在数学方法上有着相似的密切联系。将神经网络应用到纠错码的译码中，计算复杂度得到了降低，且在一定的程度上误码性能也得到了提升。

低密度奇偶检验码(LDPC码)和极化码(Polar码)是5G移动通信系统中信道编码的候选技术，也是卫星通信、军事通信等众多通信系统中信道编码的常用方法。研究基于神经网络的LDPC码和Polar码的译码方法是具有理论和实用意义的。

本文第二部分介绍了神经网络的发展过程；第三部分重点介绍基于神经网络的LDPC码和Polar码的译码方法，以及讨论了各种方法的优缺点；第四部分分析了对未来的研究方向。

2 神经网络发展历程

神经网络是由大量的神经元构成。神经元模型(如图1)是由美国心理学家McCulloch和数学家Pitts在1943年提出的，这为神经网络的理论研究开辟了崭新的道路。

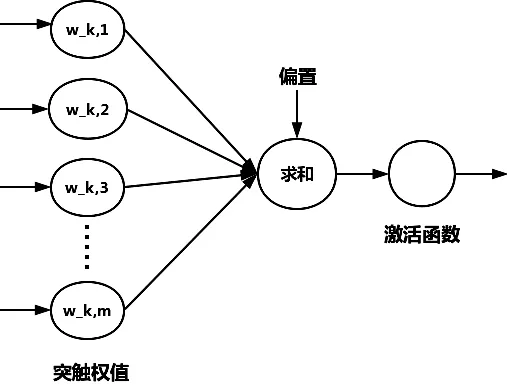
图1 神经元的模型

图1中，w_i，j表示两个神经元i和j之间的连接权值；激活函数可限制神经元输出的振幅；偏置改变激活函数的网络输入。

感知机[1]是最简单的神经网络，也是首次将神经网络和模式识别相结合的装置。由于自身结构和网络层数的限制，使得感知机对于一些复杂的异或问题没有处理的能力。

Hopfield网络模型是由Hopfield教授在1982年提出的[2]，同时还提出能量函数。Hopfield网络的出现打破了感知机的应用局限，它是一种递归神经网络，其模型可以实现联想记忆功能和作为联想存储器。

1983年，Sejnowski和Hinton提出了“隐单元”的概念，并且设计了波尔兹曼机(Boltzmann Machine，BM)[3]。BM可以从复杂的数据中发现潜在的特征并进行无监督学习，但是网络的训练时间比较长。为了减少训练时间，引入了限制波尔兹曼机(RBM)[4]，RBM可以解决分类、回归、降维等问题。

随着网络层数的增加，神经网络的逼近能力也在增强，但是网络参数的训练是一个很繁琐的过程，同时也是制约多层神经网络发展的关键因素。

1986年，Rumelhart、Hinton和Williams提出了著名的训练算法—反向传播算法(BP，Back Propagation)[5]，BP算法的出现使得神经网络的研究进入了崭新的阶段。BP神经网络的优势是在事前不知道输入和输出确定数学关系表达式时，可以通过学习来存储输入和输出之间的内在关系。

为了模拟生物神经元的局部响应特性，1988年，Broomhead和Lowe将径向基函数引入到了神经网络中，形成径向基神经网络(RBP)[6]。RBP神经网络可以实现问题的线性可分化。

由于有限的样本和计算单元导致数据间复杂函数的表现能力有限，使得一般神经网络的学习能力不强，因此，Geoffrey Hinton和Ruslan Salakhutdinov提出了深度学习的模型[7]，并证明隐含层的个数越多，网络的特征学习能力越强。深度学习建立了从底层简单特征到高层抽象语义的非线性映射关系[8]，这一研究成果推动了深度神经网络机器学习的新时代。

网络参数训练算法的不完善制约着神经网络的发展，传统神经网络中的训练算法在深度神经网络中难以完成网络的学习任务，为了解决这个问题，提出了“逐层预训练”和“精调”的训练方法[9]，使得深度学习的应用领域广泛。

3 基于神经网络的信道译码算法

神经网络最早被用于重复码和置换矩阵码的译码中，是J.C.Platt教授和J.J.Hopfield教授在1986年提出的，译码中采用的结构是Hopfield网络[10]。

随后，J.Bruck和M.Blaum提出了图码与神经网络之间存在等价的关系，并证明了线性分组码和非线性分组码的最大似然译码问题等价于求解一个神经网络收敛于它能量函数的全局极大问题[11]。

为了充分的利用分组码的代数结构，将径向基函数引入到网络中形成径向基神经网络。利用径向基神经网络[12，13]来进行译码不需要进行网络的训练，只需要将所译码的码字加入到网络中就完成了译码的过程，网络的结构简单，适用于任意长度的码字；但是此方法是以损失纠错能力为代价减少一些运算量。

在纠错码中，LDPC码和Polar码是5G移动通信系统中信道编码的候选技术，也是众多通信系统中信道编码的常用方法。基于此，重点介绍基于神经网络的LDPC码和Polar码的译码方法，总结了各种方法的优缺点，以及未来的研究方向。

3.1 基于神经网络的LDPC码译码算法

LDPC码[14]是一种具有很强纠错能力的信道编码，其校验矩阵是稀疏矩阵，即矩阵中非零元素的个数远远小于零元素的个数。

LDPC码最常用的表示方法是Tanner图(二分图)[15]。例如一个(8，2，4)的LDPC码，校验矩阵如下所示：

上述LDPC码的Tanner图如图2所示，vi表示变量节点；ci表示校验节点；两个集合的内部不存在相连的边。

图2 (8，2，4)LDPC码的Tanner图

LDPC码已有的译码算法，大部分都是基于消息置信度的迭代译码，所需的计算量高，同时还需要迭代译码计算，而且性能效果好的译码复杂度高，译码复杂度低的译码性能低，无法达成一个平衡点。将神经网络和LDPC码的译码过程相结合，充分利用彼此的优势，形成具有收敛速度快、时延稳定、并行度高的译码方法。

3.1.1 研究现状

神经网络可以作为分类器，将所有的码字存储在网络中，进行网络训练，训练结束后，将所要译的码字作为网络的输入，其译码就是将码字进行分类，即将输入的码字与存储的所有码字进行匹配。

一般线性分组码神经网络[16，17]可以实现LDPC译码算法(如图3)，该网络是由网络输入层和输出缓冲层构成。该算法的译码结构简单，易于实现；但译码性能不及标准的置信传播译码算法。对于长LDPC码，神经网络结构会变得越來越复杂，且训练所需时间过长。

图3 一般线性分组码的神经网络译码结构

图3中，神经网络有n个输入，输入端接收从信道接收到的码字信息；神经网络每层有N个神经元，代表所译码字的个数。

利用多项式神经网络可以进行LDPC码的译码[18]，译码中将多项式函数作为高阶感知器的判决函数，对于短码来说译码性能良好，但是对于长码而言，译码的复杂度、计算量和存储空间都在增加。

基于多层感知器神经网络的LDPC码译码方法[19，20]，将神经网络输入和输出的关系与LDPC码的Tanner图中的节点关系相对应，使得神经网络的复杂性得到了降低，计算复杂度也相应的降低。但网络需要大量的训练，若码长较大时，训练网络的时间就会很长，且译码性能不及置信传播译码算法。

通常训练神经网络采用的是反向传播算法，需要神经网络的每个输入序列是可见的，从而限制了译码算法的性能。为了解决上述的限制，提出了基于神经网络的LDPC码非迭代译码方法[21](如图4)，主要利用有效LDPC码的基于校验序列的行来训练网络，且识别独立的子译码结构，进行非迭代的译码。

由于一般神经网络的复杂函数的表现能力有限，网络本身的学习能力也不强。因此，提出了将平行的Hopfield神经网络和LDPC相结合的译码方法[22]，利用此方法进行译码，减少了神经网络的个数，但是由于网络是递归型神经网络，需要花费时间来达到稳定状态，不适合用在高速LDPC码中。

基于校验子生成器和LUT(Look Up Table)的LDPC译码方法[23]解决了上述方法存在的问题，译码过程不需要进行迭代计算，但是需要提前计算出每个校验子相对应的LUT(查找表)。

3.1.2 发展趋势

基于神经网络的LDPC码译码方法目前还是处于初级发展阶段，网络训练方法大都是采用反向传播算法，为了进一步提高译码的性能，降低译码的复杂程度，可利用已有的训练方法(牛顿法、共轭梯度法等)进行网络的训练，或者探究新的训练方法。

由于浅层神经网络在应用过程中，网络训练的速度比较慢，随着计算机处理速度和存储能力的提升，深层神经网络得到了快速的发展，所以可将深层神经网络应用到LDPC码的译码过程中，用于提高译码的性能。

图4 基于多层感知器前向神经网络LDPC译码器结构

3.2 基于神经网络的Polar码译码方法

Polar码[24]是第一个被证明可以达到香农容量限的编码方法，且采用持续消除(SC)译码时复杂度仅为ONlgN，其中N为码长。Polar码的基本原理就是信道极化[24]，信道极化(如图5)是由信道合并和信道分裂组成的。

图5中，W表示二进制离散无记忆信道；W-N是N个二进制离散无记忆信道W线性变换合并成的；W-N，i是W-N经过分裂转化的极化信道。

图5 信道极化现象的形成过程

对于中短码长的Polar码，SC译码算法的逐比特译码特性可能会带来错误的传播问题，所以在有限码长下译码性能不够理想。其他类型的译码算法，提升了译码的性能，但是计算量得到了增加。利用神经网络进行Polar码的译码，充分利用两者的优点，有效的减少译码的复杂度，或者提高了译码的性能。

3.2.1 研究现状

基于一般深度神经网络的译码器[25]可以通过学习大量的码字来实现接近最佳误码率的性能，但是网络的训练时间随着码长的增加呈现指数的增加，这就限制了此类译码器在长Polar码中的实际应用。

为了解决上述的问题，将上述提出的极化BP译码器中的某些字块用神经网络辅助模块来代替[26]，新译码方法的性能得到了很大的改善，但是译码的复杂性仍然很高，且硬件的高吞吐量很难实现。

传统的深度神经网络应用在Polar码的译码过程中，需要过高的网络训练和计算复杂度。将置信传播译码算法进行改进，得到多尺度置信传播译码算法，在多尺度置信传播算法的基础上建立深度神经网络[27]，得到的译码模型适用于任何形式的Polar码，训练网络时只需要很小的零码字集合，且计算复杂度与原始的置信传播算法相同。

3.2.2 发展趋势

目前Polar码是作为5G移动通信中eMBB应用场景的控制信道的编码方式，码长较短，重点研究和解决的是码长、码率灵活性问题以及编译码对信道的依赖性问题[28]。

对于长Polar码来说，利用神经网络来进行译码存在一定的困难，如网络结构的选择、硬件实施的性能。神经网络的种类很多，可以研究基于不同神经网络的深度学习Polar码译码方法，或者运用不同的训练方法来训练神经网络，使得相对应的译码性能得到提升，结构复杂度得到减少，译码的迭代次数降低。

4 结束语

本文介绍了神经网络的发展历程，以及基于神经网络的LDPC码和Polar码的译码方法，分析了每种模型方法的优缺点。由于深度神经网络的理论基础还不完善，需进行理论方面的探究和突破；其次，将不同类型的神经网络应用到不同的信道编码中，还需要进一步的研究。