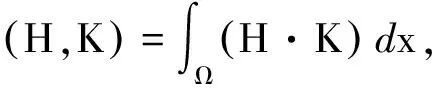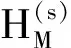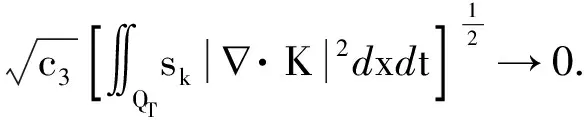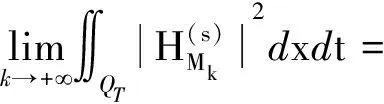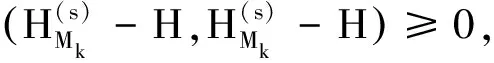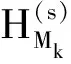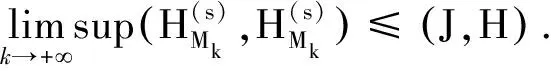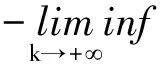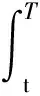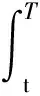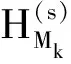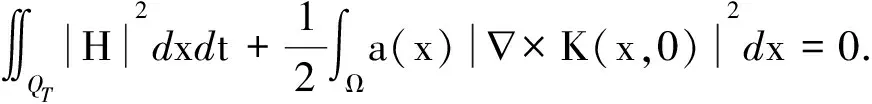一类Maxwell方程的弱解存在唯一性证明
旷雨阳,李兴华,黄宝勤
(安顺学院 数理学院,贵州 安顺 561000)
偏微分方程的基本问题之一是研究各种边值问题解的存在性.Sobolev空间[1-2]的引入为求解边值问题提供了新的有效的途径,用这种方法求出的解称为弱解或广义解[3-4].
研究弱解的存在性有很多方法,常用的有切片法、Galerkin方法、半群方法等[5-12].论文将应用Galerkin方法证明此类Maxwell方程
弱解的存在唯一性.其中:Ω∈R3为有界区域且边界∂Ω∈C1,QT=Ω×(0,T],ST=∂Ω×(0,T] ,N为 ∂Ω的单位外法向量,H=(H1,H2,H3)∈(L2(Ω))3为向量值函数,G(x,t)和H0(x)分别为给定的边界条件和初始条件.
1 预备知识
定义1[4]如果赋范空间X到它的第二共轭空间X**的自然映射T是满射的,则称X是自反的,记作X=X**.

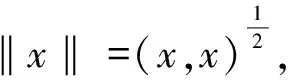

(1)‖An‖有界;
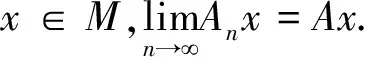
2 假设条件
H(2.1) (1) 设函数a(x,t)在QT关于t可微且存在常数r0,R0,使得
0 (2) 向量值函数G(x,t)满足G(x,t)∈H1(0,T;H(curl,Ω)),Gt(x,t)∈(L2(QT))3. (3)H0(x)∈H0(curl,Ω)∩(L(Ω))3. (4)F(x,t)∈H1(0,T;H(dir,Ω)). 其中 H(curl,Ω)={G(·)∈(L2(Ω))3:×G∈(L2(Ω))3}, H0(curl,Ω)={G(·)∈(L2(Ω))3:×G∈(L2(Ω))3,N×G=0,x∈∂Ω}, H(dir,Ω)={G(·)∈(L2(Ω))3:·G∈(L2(Ω))3}. 定义3若向量值函数H(x,t)满足: (1)H-G∈L2(0,T;H0(curl ,Ω));(2) 对任意的函数K(x,t)∈H1(0,T;H0(curl,Ω)),K(x,T)=0,a.e,x∈Ω,有 则称H(x,t)为问题(1)~(3)的弱解. 考虑如下初边值问题的解的存在性 定义4若向量值函数H(x,t)满足 (1)H∈L2(0,T;H0(curl,dir,Ω)); (2) 对任意的函数K(x,t)∈H1(0,T;H0(curl,Ω)),K(x,T)=0,a.e,x∈Ω,有 则称H(x,t)为问题(4)~(6)的弱解,其中:H0(curl,dir,Ω)=H0(curl,Ω)∩H(dir,Ω). 首先考虑如下特征值问题 现构造如下近似系列:对一个给定的正整数M>0,定义 (7) (8) (9) djM(0)=hj,j=1,2,…,M. (10) 根据常微分方程组解的存在性,(9)、(10) 为线性常微分方程的初值问题,故存在唯一的解,因此djM(t) 被方程组 (9)、(10) 所决定,且 引理1假设H(2.1) 成立,则存在正常数c3和c4,有 (11) (12) 其中:c3,c4仅依赖于已知数据,但不依赖于M. (13) (14) (15) 定理3若假设H(2.1) 满足,则问题 (1)~(3) 有唯一的弱解H(x,t)∈L(0,T;H0(curl,Ω))∩L(0,T;(L2(Ω))3),进一步有Ht∈(L2(QT))3. 对任一试探函数K(x,t)∈H1(0,T;H0(curl,Ω)),满足K(x,T)=0,有 (16) 当sk→0时,由柯西不等式和引理1,有 类似地,当sk→0时,有 因此,在(16) 式中,两边令sk→0,有 (17) ∬QT(FM·Kk)dxdt, 故Is>0. 又 根据Banach-Semhaus定理,有 又对任意的试探函数K(x,T)=0,有 ∬QTat|×K*|2dxdt+∬QTF·K*dxdt. 因此,有 (18) 由(17)、(18)式,有 ∬QTJ·Hdxdt. (19) 现证明在QT中一致有J(x,t)=H(x,t). 对任意的向量w(x,t)∈(L2(QT))3,有 即 故∬QT[J-w]·[H-w]dxdt≥0. 取w=H+δV,V∈L2(QT)为任意向量,δ为任意数,则-δ∬QT[J-H-δV]Vdxdt≥0,由δ的任意性,有 ∬QT(J-H-δV)Vdxdt=0. 令δ→0,有∬QT[J-H]·Vdxdt=0,由V的任意性,有 J(x,t)=H(x,t),a.e,(x,t)∈QT, 这就证明了解的存在性. 下面证明解的唯一性:设H1(x,t)和H2(x,t)为问题(1)~(3)的两个弱解,令 H(x,t)=H1(x,t)-H2(x,t), 则对任意的试探函数K(x,t)∈H1(0,T;H0(curl,Ω)),有 ∬QT[-H·Kt+a(x)(×H)·(×K)] dxdt=0. 令 (x,t)∈QT, 则K(x,t)∈H1(0,T;H0(curl,Ω)),且K(x,T)=0,(K(x,t))t=-H(x,t),×H=-×(K(x,t))t,故因为×K(x,T)=0,x∈Ω,故3 弱解的定义及近似解的构造
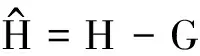
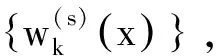
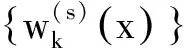
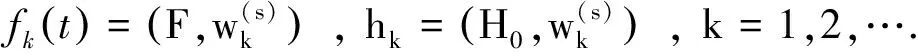
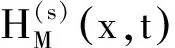
4 弱解的存在唯一性证明