一种增强全局搜索能力的差分进化算法

范宇凌

（华侨大学工学院，泉州 362021）

0 引言

差分进化算法（Differential Evolution，DE）是一种通过模拟种群进化差异的启发式随机搜索算法[1]。Storn和Price最初设想是解决Chebyshev多项式问题，后来发现较之其他进化算法，DE算法在解决复杂的全局优化问题方面的性能更加突出，过程也更为简单，受控参数少，适应性强。目前在解决实际优化问题方面得到了广泛的应用，例如过程模拟、工程设计优化、经济和环境分配优化等[2]。

此外，DE算法的性能高度依赖于变异策略和控制参数。例如，种群规模NP，放缩因子F和交叉常量CR。通常来说，DE算法解决不同的优化问题所需的最合适的变异策略和控制参数是不同的。即使对于一个特定的优化问题，在进化过程中所需的最佳策略和控制参数可能会有所不同。特别是在解决各类优化问题，使用传统的反复实验法来确定最佳策略和参数虽是有效的，但是耗时。

为了解决上述问题，国内外学者对标准差分进化算法（DE）提出了众多改进，大致包含以下几个方面：控制参数的自适应，变异策略的改进，多策略的使用以及从维持种群多样性角度出发进行的算法改进。例如，jDE算法提出一种自适应控制参数的差分进化算法[3]；SaDE算法采用一种适应性变异策略和参数[4]；王勇设计了一种多策略和参数组合的试验池的差分进化算法[5]；JADE算法提出一种基于“current-to-pbest/1”变异策略和自适应参数的差分进化算[6]；DE-DPS算法提出一种动态选择最佳的参数组合的差分进化算法[7]；CoBiDE算法引入了协方差矩阵学习和双峰式分布参数调整对差分进化算法进行改进[8]；EPSDE算法提出一种变异策略和参数集合的差分进化算法[9]；MPEDE算法提出了一种基于多种群的方法来实现多策略和参数组合的差分进化算法[10]，其将种群分成多个子种群，利用子种群与相应的策略和参数集合相结合，来增强种群多样性与改善种群单一策略带来的不利影响，然而没考虑到种群的是否出现停滞和早熟，以及收敛速度会降低的情况。

考虑到算法的整体优化效果，为了进一步提高算法的收敛性和鲁棒性，以及子种群的停滞现象，本文结合种群进化的进程速度来实现策略加权，提出了一种增强全局搜索能力的差分进化算法（MPWDE）。本文首先简单介绍了标准差分进化算法的原理和步骤，接下来详细阐述了算法的改进工作，包括种群变化，变异策略的改进，构造加权变异策略和动态递增参数，并在基准测试函数上对MPWDE算法实现30和50维的仿真测试且与其他算法作了比较，最后对本文的工作进行了总结。

1 差分进化算法

1.1 初始化

设种群规模为NP，可行解空间的维数为D，用XG来表示进化到G代时的种群，记为每一个个体是由D维参数构成，可表示为：

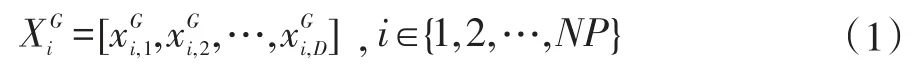
其中分别表示上界和下界。

1.2 变异操作

变异操作是差分进化算法中最重要的步骤，在这一阶段，父代种群中的个体通过变异策略产生变异个体在DE中常用的差分策略为随机选取种群中两个不同个体将其向量缩放后与待变异个体进行向量合成，即：

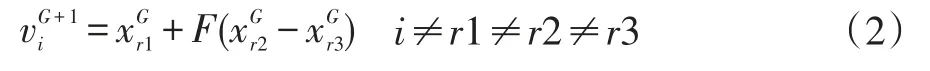
其中，F为缩放因子，其取值通常在[0,1]内，控制偏差向量的放大作用；第一部分为随机选取的待扰动基向量，第二部分是对第一部分起扰动作用的差分向量。

1.3 交叉操作

交叉操作的主要作用是生成的变异个体与原种群里面的个体进行交叉操作，从而生成新的交叉个体。DE算法采用的是二项式交叉方案，交叉操作如下：

其中，randb是[0,1]间的随机数；CR是范围为[0,1]的常数，称为交叉常量，CR的取值范围越大，发生交叉的可能就越大，CR=0表示没有交叉；randr(j)是在[1,D]随机选择整数。

1.4 选择操作

选择操作主要采用优胜劣汰的贪婪选择模式，使得子代个体总是优于或等于父代个体，当且仅当新的向量个体ui的适度值要比目标向量个体的适度值更好时，新的向量个体ui才会被种群接受。否则，xi仍保留在下一代种群中，并在下一次迭代计算中继续作为目标向量执行变异及交叉操作，从而使种群始终向最优解的方向进化。选择操作如下：

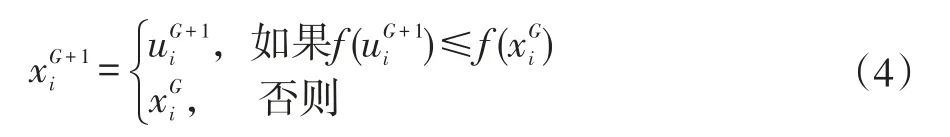
式中 f(X)为所要优化的目标函数。

2 一种增强全局搜索能力的差分进化算法

2.1 种群多样性

根据标准DE算法的原理，随着迭代次数的增加，个体间的差异性逐渐减小，形成“聚集”现象，导致在搜索全局最优时过早收敛，而使算法陷入局部最优。本文引入了整体种群划分子种群的思维，通过每一次迭代中子种群的进化结果来划分下一代子种群的个体数量，所以多种群方法更能保证种群的多样性，避免种群的单一性促使算法早熟。

假设整体种群为Pop，Popi为Pop的子种群，NPi为Popi的种群规模，λi为子下种群规模比例，下面给出其定义：

其中，λi的取值范围分布在[0,1]之间。

本文中多种群的规划为：首先把整体种群分成三个子种群分别为 Pop1、Pop2、Pop3，Pop1种群规模比Pop2、Pop3种群规模大，每一子种群采用不同的变异策略，统计子种群经过每一次种群进化后edp_num1、edp_num2和edp_num3（保留下优良个体维数的总和），根据种群个体的维数D,可得出子种群优良率rate1、rate2和rate3。将三个子种群的种群优良率进行比较得出优良率高的策略，下一次进化过程中分配的种群规模为NP1。

2.2 加权变异策略

变异策略是DE算法的核心，根据变异机制的不同，产生多种策略。为区分不同的DE变异策略，一般表示为DE/X/Y/Z，其中DE代表差分进化算法；X表示待扰动的基向量，它既可以是当前种群中的随机向量（rand），也可以是当前种群的最优向量（best）；Y 表示差分向量个数；Z指代所采取的交叉模式。本文通过三个子种群在进化过程中采样不同的变异策略来保证种群个体的多样性。从以往改进过的DE经典算法中学习，选出三个使用较为广泛的策略：

（1）“DE/current-to-best/1”

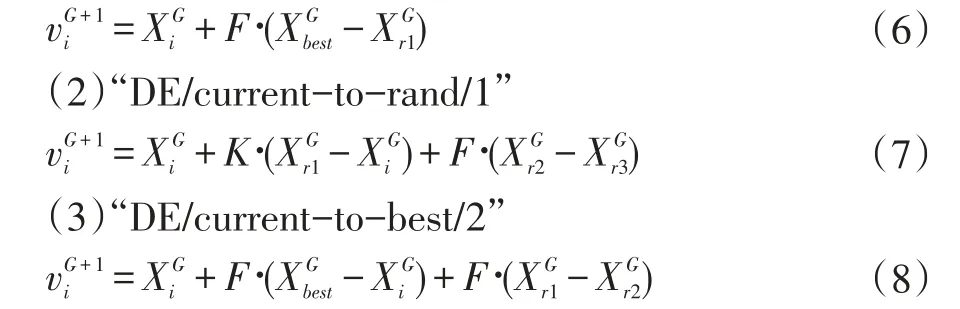
式（2）中所有参与变异的向量均以随机的方式被选择，因此能够在全局进行寻优，但是由于缺少最优解信息，使得式（2）收敛速度较慢。式（3）、（4）通过当前最优解来寻求全局最优解，在进化过程虽然能将搜索范围缩小至最优解附近加快算法的收敛速度，但种群多样性缺失，不能找到最优解。为减小式（4）前期搜索范围狭小，后期收敛速度慢的影响，对式（4）变异策略进行修改，建立加权变异策略机制。对种群的每一个体建立两种变异：局部变异和全局变异，改进后的变异策略如下：

局部变异：

其中，表示Pop1种群中的最佳个体，XGbest表示Pop种群中的最佳个体，r1、r2∈(1,NP1)。

结合这两种变异模式，采用随机变化的变量w∈(0,1)作为权重对局部和全局变异成分进行加权平均形成新的变异策略，设t为当前函数评估次数，FES函数最大评估次数，可表示为：

其中，wmin、wmax为权重因子w上下界，且wmin、wmax∈[0,1]。算法开始时，t=0，w=wmin，随着当前评估次数的增大，w逐渐增大，最终当t=FES达到最大wmax。算法开始以局部搜索模式为主，然后过渡到全局模式。显然为了达到局部变异和全局变异的平衡，合理选择适当的wmin和wmax是非常必要的。本文中wmin=0、wmax=1。

2.3 算法步骤

（1）初始化种种群：根据公式（5）将种群分成三个子种群 Pop1、Pop2、Pop3，gen=0，设置 wmin、wmax的值，迭代次数置为0。

（2）计算当前种群适度值 f。

（3）根据公式（6）、（7）、（11）进行变异操作。

（4）进行交叉选择操作。

（5）计算优良率rate1、rate2和rate3。

（6）判断迭代次数是否到达最大值，到达继续执行步骤（7），反之则重新分配子种群并返回步骤（2）进行循环迭代。

（7）输出适应度值最优的个体。

3 实验结果与分析

3.1 实验设置

为了验证本文提出的MPWDE算法的性能，采用基准测试函数中5个测试函数，对该算法进行测试。将MPWDE与其他5个经典的DE算法对比，包括jDE、JADE、SaDE、EPSDE、MPEDE。选择上面几个 DE算法的原因如下：第一，文献[3，6]中的JADE和jDE常被引用作为基准算法；第二，文献[4，9]中SaDE和EPS⁃DE包含着几个类似的策略；第三，文献[10]中的MPEDE是目前效果最好的DE算法。这些算法的所有变异策略和控制参数的设置都与原始参考文献中所给出的变异策略和控制参数相同。为了提供一个更全面的比较，本文设置种群规模NP=250，分别对30维和50维的情况进行实验，且每个算法对每个测试函数独立运行25次，FES分别设置为300000和500000。实验环境：操作系统：Win7专业版64位，CPU：Intel Core i7（3.40GHz），RAM：8GB，语言：MATLAB ，编译器：MAT⁃LAB R2014b。

3.2 算法有效性分析

以下是可行解为30维和50维的实验结果，如表1和表2所示，表中提供了实验结果的平均误差和标准偏差（在括号中）。标记“+”、“-”和“≈”表示比较算法性能明显好于、明显差于和近似于MPWDE。

由表1可知，对于测试函数F1-F5，虽然JADE和MPEDE算法实验效果表现较好，但是MPWDE的实验效果更佳，结果差别更加显著；在测试函数F3、F4和F5上，MPWDE的实验结果明显优于JADE和MPEDE算法；在测试函数F1和F2上，MPWDE与对比算法是可比较的。

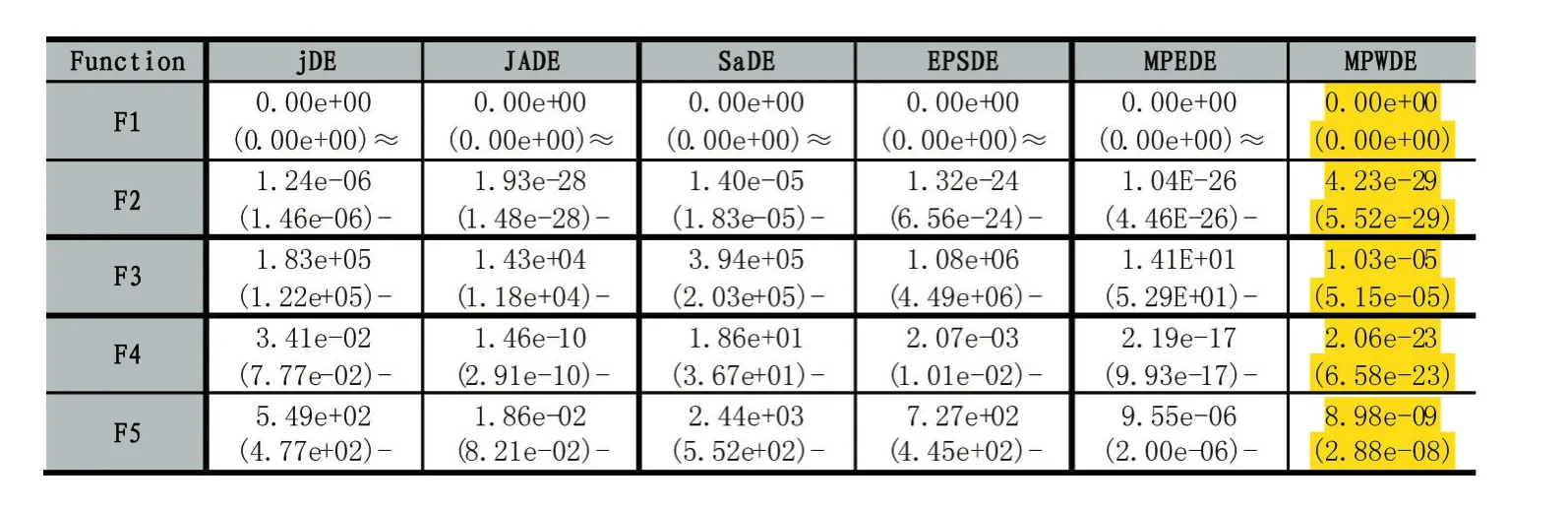
表1 可行解为30维的标准测试函数计算结果

表2 可行解为50维的标准测试函数计算结果

由表2可知，对于测试函数F1-F5，F0函数的实验效果相近，虽然JADE和MPEDE算法实验效果在F2和F3表现较好且MPWDE的实验效果稍逊点，但是MPWDE在F4和F5的实验效果要优于所有对比算法。

通过进化曲线评价算法性能，分析表1、表2的数据。进化曲线以平均适应度误差值（Average Function Value）为纵轴，评估次数FES为横轴，具体分析如图1-图6所示。

通过五种经典DE算法和MPWDE进行对比表明，MPWDE的不管在收敛速度还是在收敛性能方面都具有很强的优越性。图1测试函数F2，jDE和SaDE策略单一导致种群变异差异较小且出现早熟，ESPDE、JADE和MPEDE均未出现收敛趋势，但是求解精度不及 MPWDE。图 4测试函数 F5，jDE、SaDE和 ESPDE均出现早熟，而JADE和MPEDE虽然在迭代中也有机会寻找全局最优解，但是精度不高且收敛速度远比不上MPWDE。从图5和图6，MPWDE算法进化前期在进行全局搜索收敛速度缓慢，后面逐步过渡局部搜索从而提高求解精度。不仅如此，从图2、图3和图4测试函数可以明显看出MPWDE的收敛速度和求解精度都是最优的。种群多样性可以从图1至图6看出，当种群失去多样性的时候，算法就会出现早熟，虽然种群多样性和收敛速度是矛盾的，但是本文算法不仅控制种群的多样性，还应用了加权策略使搜索从全局到局部，因而算法在求解精度、收敛速度方面都优于另外五种算法。

4 结语

实际优化问题往往具有未知性、复杂性、高维等特性，标准差分进化算法过程较为简单、受控参数少、策略单一，无法不断地提高自身对外界环境的适应程度，逐步逼近问题的最优解。本文从种群多样性的理论角度出发，提出了一种增强全局搜索能力的差分进化算法，通过多种群机制有效改善了种群多样性，引入权重因子叠加双变异策略使改进后的算法逐步从全局搜索过渡到局部搜索。通过交叉因子动态递增的调整策略，避免了复杂的参数反馈过程，提高了算法收敛速度，改善了DE算法在收敛速度和搜索鲁棒性之间存在的矛盾，通过基准测试函数的仿真结果并与其他算法比较，表明MPWDE有较强的全局搜索能力，能有效避免早熟收敛，在算法的运行速度和求解精度方面都有了进一步的提高。

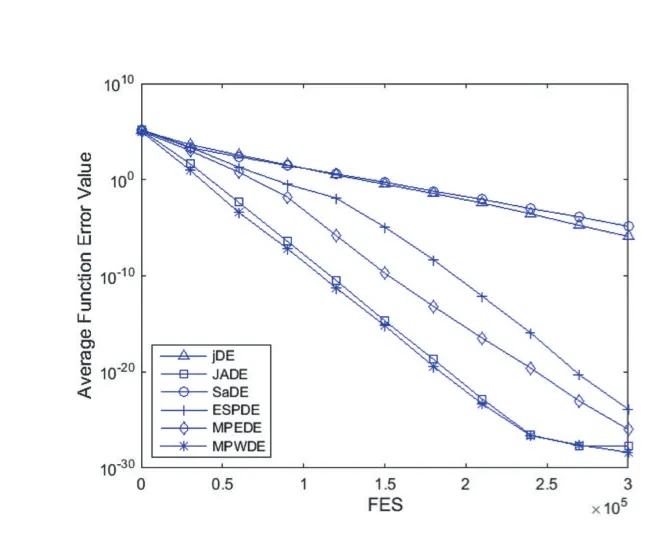
图1 30维F2函数平均适应度误差曲线

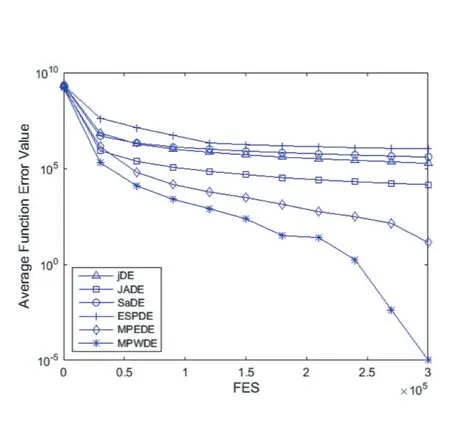
图2 30维F3函数平均适应度误差曲线

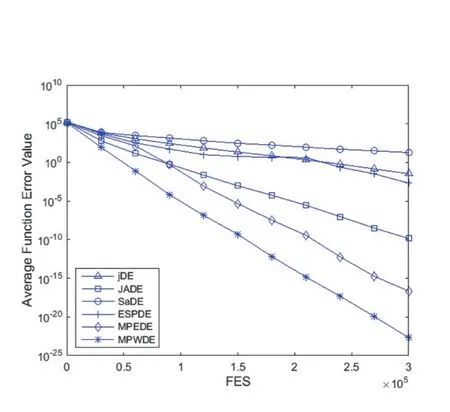
图3 30维F4函数平均适应度 误差曲线

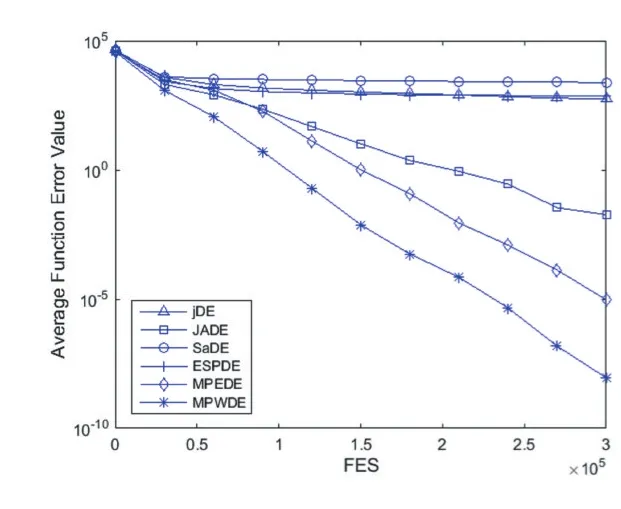
图4 30维F5函数平均适应度误差曲线

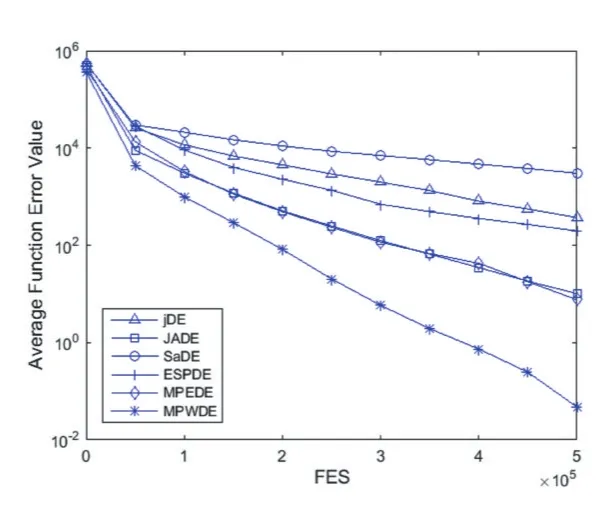
图5 50维F4函数平均适应度 误差曲线

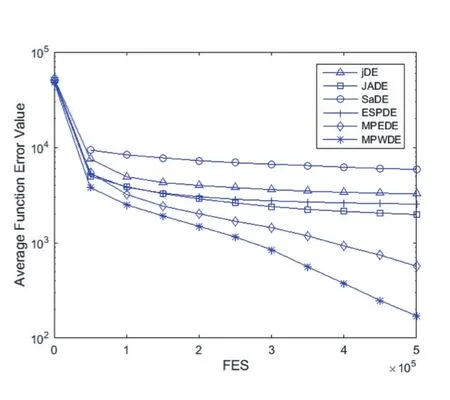
图6 50维F5函数平均适应度 误差曲线

[1]Storn R,Price K.Differential Evolution—A Simple and Efficient Heuristic for Global Optimization Over Continuous Spaces[J].Journal of Global Optimization,1997,11（4）:341-359.

[2]刘波,王凌,金以慧,等.差分进化算法研究进展[J].控制与决策,2007,22（7）:721-729.

[3]Breast,J.,Greiner,S.,Boskovoic,B.,Mernik,M.,Zumer,V..Self-Adapting Control Parameters in Differential Evolution:A Comparative Study on Numerical Benchmark Problem[J].IEEE Transactions on Evolutionary Computation,2006,10（6）:646-657.

[4]Qin,A.K.,Huang,V.L.,Suganthan,P.N..Differential Evolution Algorithm With Strategy Adaptation for Global Numerical Optimization[J].IEEE Transactions on Evolutionary Computation,2009,13（2）:398-417.

[5]Wang,Y.,Cai,Z.,Zhang,Q..Differential Evolution with Composite Trial Vector Generation Strategies and Control Parameters[J].IEEE Transactions on Evolutionary Computation,2011,15（1）:55-66.

[6]Zhang,J.,A.C.,S..JADE:Adaptive Differential Evolution With Optional External Archive[J],IEEE Transactions on Evolutionary Computation,2009,13（5）:945-967.

[7]Sarker,R.A.,Elsayed,S.M.,Ray,T.,Differential Evolution With Dynamic Parameters Selection for Optimization Problems[J].IEEE Transactions on Evolutionary Computation,2014,18（5）:689-707.

[8]Wang,Y.,Li,H-X.,Huang,T.,Li,L.,Different Evolution Based on Covariance Matrix Learning and Bimodal Distribution Parameter Setting[J].Applied Soft Computing,2014,18（1）:232-247.

[9]Mallipeddi,R.,Suganthan,P.N.,Pan,Q.-K.,Tasgetiren,M.F..Differential Evolution Algorithm with Ensemble of Parameters and Mutation strategies[J].Applied Soft Computing,2011,11（2）:1679-1696.

[10]G.H.Wu,R.Mallipeddi,P.N.Suganthan,R.M.Duwairi,R.G.Reynolds,Differential Evolution with Multi-Population Based Ensemble of Mutation Strategies[J].Information Sciences,2016,10（C）:329-345.