基于Maxwell的永磁同步电动机最佳电流控制特性曲线绘制方法

，，

(中车株洲电机有限公司，湖南株洲 412001)

0 引言

永磁同步电机定子电流最佳控制[1、2]是一种在不超出逆变器供电极限能力的情况下，通过控制电流矢量使电机在整个运行范围内输出最大电磁功率的控制策略。在该控制策略下得到的电磁转矩、输出功率、定子电流等参数随转速变化的特性曲线，成为衡量永磁同步电机最大出力能力和选择电机型号的重要依据。Ansys Maxwell是一款用于电机电磁方案设计和性能仿真的的重要工具，并已受到国内外学者的青睐。最初Ansys Maxwell仅用于电机的本体设计及磁场性能的分析，例如崔薇佳[3]等采用Ansys Maxwell软件仿真了不同的电磁方案，实现了减小齿槽转矩的目的。魏曙光[4]等基于Ansys Maxwell软件设计了一种定子双绕组的复合发电系统。随着Ansys Maxwell应用技术的不断发展，出现了在研制阶段就开始关注电机的外特性及控制策略的研究成果。Takashi ABE 等[5]在Ansys Maxwell的Simploer应用模块中搭建了DSP(数字信号处理Digital Signal Processing)控制模块PWM(脉宽调制Pulse Width Modulation)信号生成模块、PWM逆变模块及高速电机模块，实现了场路双向耦合计算。Ling[6]等基于Ansys Maxwell软件建立了开关磁阻电机的有限元模型，研究了不同控制策略时电机的动态特性，并借助与Matlab结果的对比，验证了其方法的正确性。但是，通过Ansys Maxwell与Simploer联合仿真，需要耗费大量的计算时间。因为在Simploer控制电路的每一个时间步内，都要在Ansys Maxwell 2D中进行一次电磁场计算。而且，要研究电机的最佳电流控制等控制特性，就要在Simploer中搭建复杂的控制电路，这给非电机控制专业的工程设计人员带来很大困扰。另外，Ansys公司也推出了可以单凭Ansys Maxwell就能仿真转矩-转速特性曲线的工具包(Electric Machines Design Toolkit)，但该工具包需要额外购买。因此，仍然需要深入研究基于Ansys Maxwell软件绘制定子电流最佳控制特性曲线的方法。

为此，根据定子电流最佳控制策略的基本原理，提出基于Ansys Maxwell软件的特性曲线绘制方法。以某型永磁同步电动机为研究对象，采用Ansys Maxwell软件计算满足最大转矩/电流及普通弱磁控制策略时所对应的电流矢量有效值、内功率因数角，进而绘制电机的转矩、输出功率、d轴电流、q轴电流随转速的变化曲线。为验证文中方法的正确性，对比分析Ansys Maxwell仿真值与Matlab解析解的结果。

1 最佳电流控制特性曲线绘制方法

1.1 基于Maxwell查找定子电流的最佳控制工作点的方法

(1)最大转矩/电流控制

以额定工作点的电压作为电压极限值，在保持额定工作点电流有效值和内功率因数角不变的条件下参数化扫略转速即可。

(2)弱磁控制

在某一转速时参数化扫掠电流有效值和内功率因数角，再通过相电压-转速曲线插值查找满足最大电压极限条件的所有电流有效值和内功率因数角，进而找到电磁转矩最大值所对应的电流有效值和内功率因数角。当电流有效值等于额定电流的有效值时，表明电机运行于普通弱磁区；当电流有效值小于额定电流的有效值时，表明电机运行于最大输出功率弱磁区。

当仅存在普通弱磁控制时，在额定电流有效值条件下，参数化扫掠电机转速和内功率因数角即可找到满足电压极限条件的内功率因数角，进而求出相应的电磁转矩。但若存在最大功率弱磁控制，该方法将不能得出普通弱磁控制的极限转速。

1.2 基于Ansys Maxwell的定子电流的最佳控制仿真算例

为验证上述方法的有效性，以某型号永磁同步电动机为研究对象具体展示文中方法在Ansys Maxwell中的应用过程。其中，在进行仿真计算时，考虑到热负荷的限制，将电机额定电压作为极限电压，额定电流作为极限电流。

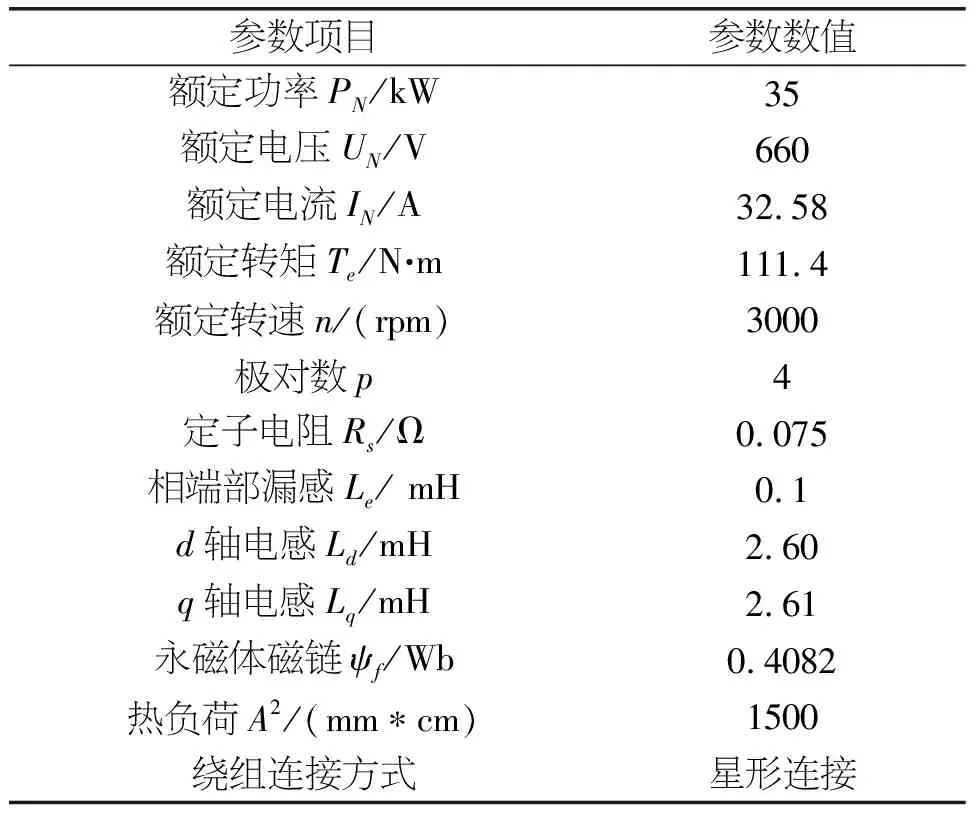
表1 某型号永磁同步电动机的电磁参数

在Ansys Maxwell中电机二维几何模型如图1所示。

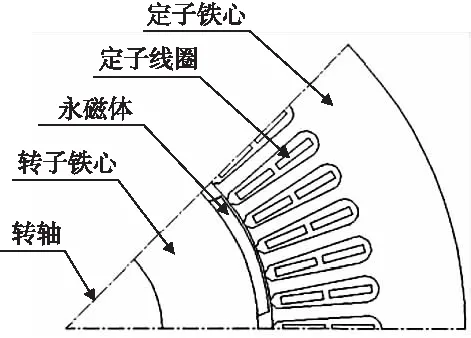
图1 某型号永磁同步电动机模型

1.2.1 求额定工况的运行点

(1)对齐A相轴线和永磁体N极轴线

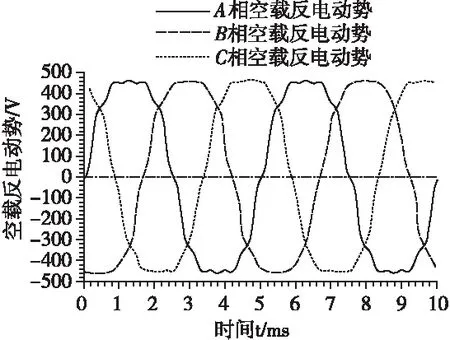
图2 空载反电动势随时间变化曲线

在电流源激励下求出空载反电动势随时间的变化曲线见图2。在t=0时刻A相空载反电动势通过原点，表明A相轴线与永磁体N极已经对齐。

(2)额定工作点

设置额定电流的有效值为32.58A且额定转速为3000r/min，在-90°～90°范围内参数化扫掠内功率因数角，仿真计算后输出电磁转矩平均值随内功率因数角变化曲线见图3。通过查找该曲线上的最大电磁转矩(111.8Nm)，从而找到额定工作点所对应的内功率因数角(0°)。

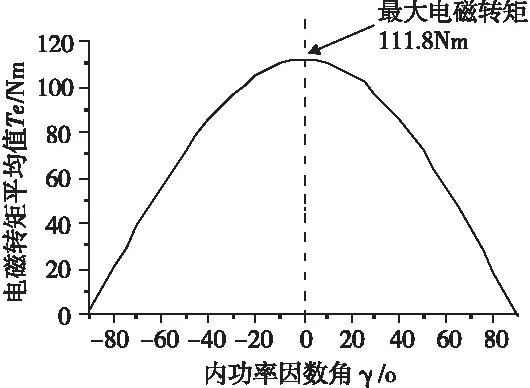
图3 求取额定工作点

1.2.2 满足最大转矩/电流控制的工作点

在额定电流有效值为32.58A及内功率因数角为0°条件下，在0～3000r/min范围内参数化扫掠转速。仿真结束后按式(1)求出A相的相电压瞬态值U(t)

(1)

式中，i(t)—A相的定子电流瞬态值；ψ(t)—A相的瞬态磁链。

进而得到A相绕组的相电压有效值随转速的计算结果如图4、图5所示。

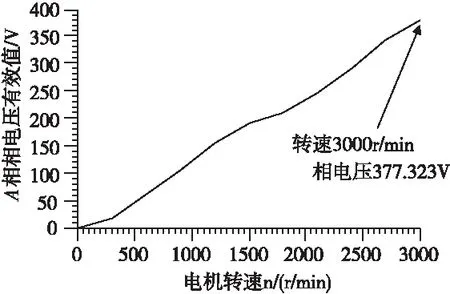
图4 最大转矩/电流区相电压随转速的计算结果

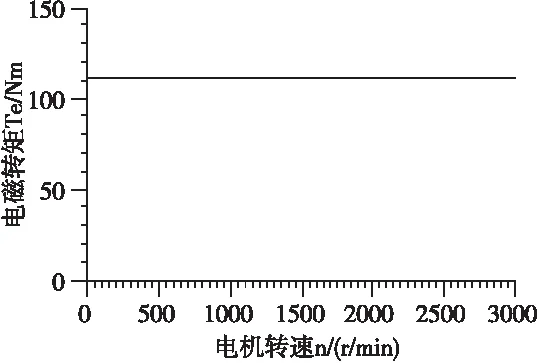
图5 最大转矩/电流区电磁转矩随转速的计算结果

由图4可知，转速从0r/min增至3000r/min，A相绕组的相电压从0V增加至377.323V。在额定转速3000r/min时，比额定相电压381.05V仅低约1%。

由图5可以看出，当转速从0r/min增至3000r/min时，电磁转矩几乎为定值,平均值约为111.7Nm，仅比额定转矩111.4Nm大约0.27%，与最大转矩/电流控制条件下电机输出恒定转矩的常识相符，表明采用文中方法可以正确计算出满足最大转矩/电流控制的工作点。

1.2.3 满足普通弱磁控制的工作点

(1)以转速为3600r/min为例，按文中方法找到该转速下满足普通弱磁控制的工作点。

参数化扫掠定子电流有效值，部分计算结果如图6、图7所示。在图6中，根据A相绕组相电压有效值381.05V，可查找不同电流有效值所对应的内功率因数角。例如，电流有效值为32.58A时所对应的内功率因数角为25.46°。进而在图7中，查出相应的电磁转矩为100.82Nm。

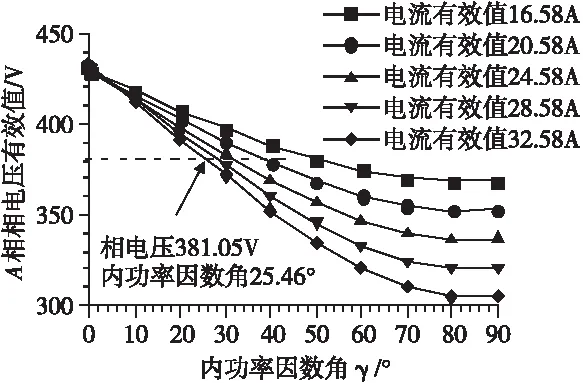
图6 弱磁区的工作点

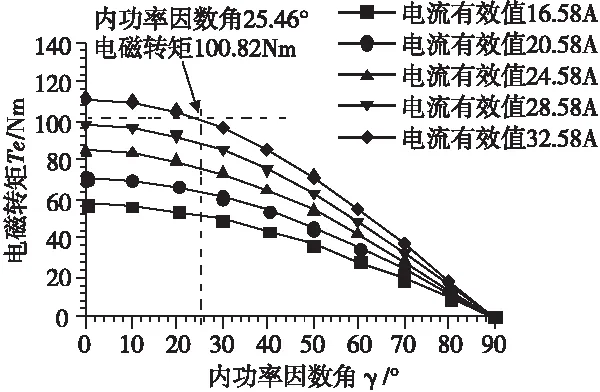
图7 弱磁区工作点所对应的电磁转矩

(2)将3600r/min转速下的计算结果汇总于表2。

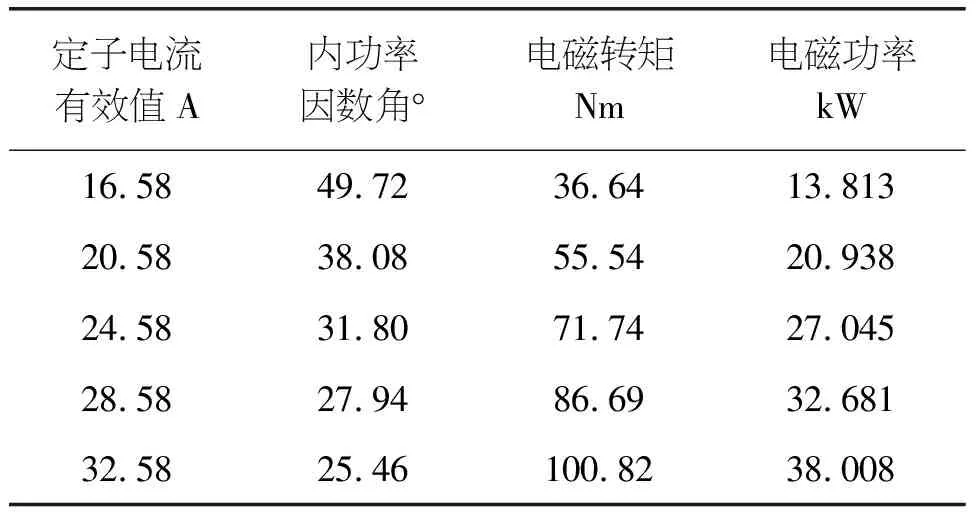
表2 普通弱磁区工作点的部分数据(3600r/min)

由表2可知，随着电流有效值从16.58A增至32.58A，内功率因数角从49.72°减至25.46°，电磁转矩从36.64Nm增至100.82Nm，电磁功率从13.813kW增至38.008kW。可见当电流矢量的有效值达到额定值32.58A，内功率因数角为25.46°时，电磁转矩最大、相应的电磁功率也最大，电动机运行在普通弱磁区。

(3)重复应用上述方法，找到不同转速下的电流有效值和内功率因数角，并计算出相应的电磁转矩、电磁功率、直轴电流及交轴电流，再将所得结果见表3。

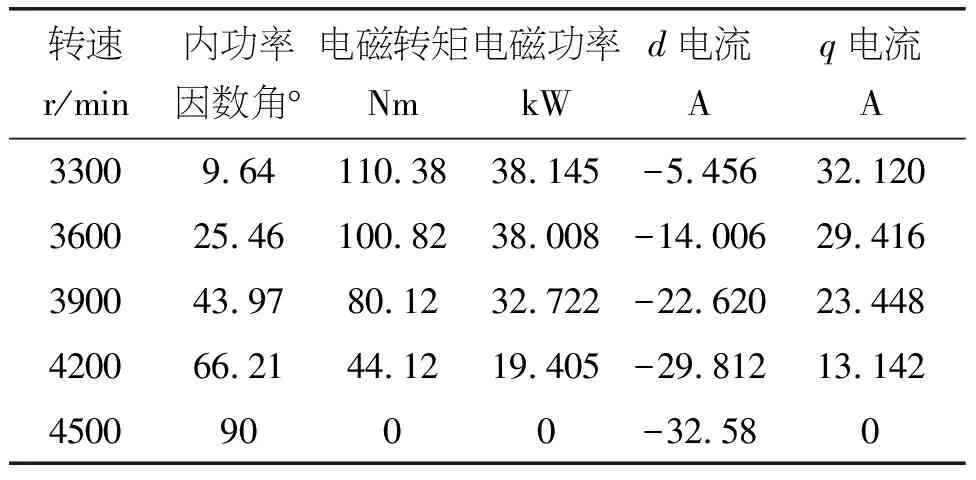
表3 普通弱磁区电机性能随转速变化的部分数据

其中，计算直轴电流及交轴电流的公式如下所示。

Id=-Issin(γ)

Iq=Iscos(γ)

(2)

式中，Id—d轴电流；Iq—q轴电流；Is—定子电流有效值；γ—内功率因数角。

2 特性曲线的对比分析

根据图4和表3中数据绘制了电磁转矩、电磁功率、d轴电流及q轴电流随转速变化的特性曲线，如图8、图9所示。采用表1中给出的电磁参数，并根据文献[1]中的相关理论计算出了相应的解析解。Ansys Maxwell仿真值与Matlab解析解的对比分析如下。

2.1 电磁转矩及电磁功率对比分析

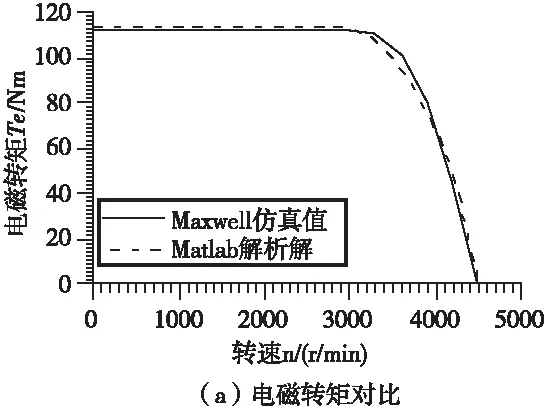
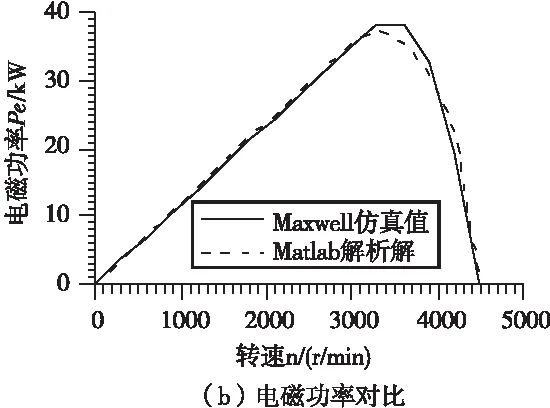
图8 电磁转矩及功率随转速变化特性曲线的对比

从图8中可以看出，当转速从0r/min增至3000r/min时，采用Ansys Maxwell计算出的电磁转矩几乎恒定不变，约为111.7Nm；电磁功率随转速线性增至35.091kW。当转速达到4500 r/min时，电磁转矩降至0Nm；电磁功率先增至38.145kW再降至0kW。在整个速度范围内，Ansys Maxwell仿真值与Matlab解析解的电磁转矩和电磁功率基本吻合。

2.2 定子电流对比分析

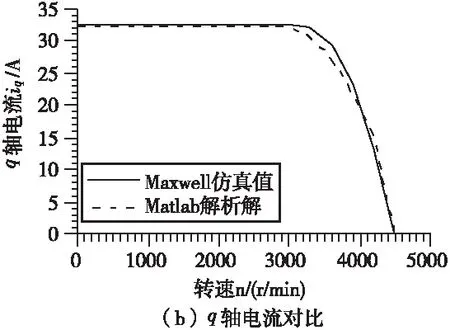
图9 d、q轴电流随转速变化特性曲线的对比

从图9中可以看出，转速从0r/min增至3000r/min，Ansys Maxwell计算出的d轴电流恒为0A，q轴电流恒为32.58A，与表贴式永磁电机最大转矩/电流控制即是id=0控制的理论相符。在整个速域内，Ansys Maxwell仿真值与 Matlab解析解的d轴电流和q轴电流随转速变化的趋势完全一致。

以上对比结果表明，文中提出的采用Ansys Maxwell软件得出定子电流的最佳控制特性曲线的方法是正确有效的。而且，与解析计算相比，采用AnsysMaxwell软件可以研究特定工作点时电机内部磁场的分布情况，还可以考虑铁心饱和、涡流损耗对电感、磁链的影响。所以AnsysMaxwell仿真值比解析解的精度更高，结果更为可信。但文中所选永磁同步电动机仅存在最大转矩/电流控制区及普通弱磁控制区，所以还需进一步验证文中关于最大输出功率弱磁控制工作点查找方法的正确性。

3 结语

根据定子电流的最佳控制的基本原理，提出了基于Ansys Maxwell软件的特性曲线绘制方法。以某型永磁同步电动机为研究对象，按文中方法计算了最大转矩/电流及普通弱磁控制时对应的电流矢量有效值、内功率因数角及转速，进而绘制了电机的转矩、输出功率、d轴电流、q轴电流随转速的变化曲线。借助Ansys Maxwell仿真值与Matlab解析解的对比，结果表明两者随转速的变化趋势一致。这意味着文中提出的采用Ansys Maxwell软件仿真定子电流的最佳控制特性曲线的方法是正确有效的。