一种直驱永磁电机分数槽绕组的设计与分析

(中车永济电机有限公司特种产品开发部，陕西西安 710018)

0 引言

随着近年来电力电子的快速发展，其拓扑结构不断变化，永磁电机的应用领域也越来越宽广。特别是对于一些去除齿轮箱的直驱系统，电机与负载直接相连，因系统结构简单和总损耗减少，直驱永磁电机越来越被市场看好。

当永磁电机旋转时，由于定子铁心开槽导致主磁路中磁阻发生变化，由永磁体与定子齿间相互作用从而产生了齿槽转矩[1]。齿槽转矩的产生导致永磁电机的转矩波动，使电动机运行时产生振动，并使电机的可控性变差。因此对于永磁电机，很有必要对减少齿槽转矩采用有效的措施[2]。

对于内置式直驱永磁电机，可以通过采用极数与定子槽数配合、增大气隙长度、定子斜槽或转子斜极、气隙磁密波形优化等多种方法来实现[1]。本方案通过采用双层短距分布式分数槽绕组，有效的削弱了齿谐波和齿槽转矩，使反电势波形谐波含量减少，使电机负载运行时转矩波动达到工业使用要求。

1 常用交流绕组

电机定子中的交流绕组一般原则是[2]：(1)由绕组合成的磁动势及电动势在空间波形分布上尽量接近正弦波形；(2)其基波磁动势和基波电动势力求最大；(3)既要节省铜材也要把损耗控制在合理范围内；(4)对多相绕组其各相磁动势和电动势要对称，电阻和电抗要平衡。

对于永磁电机，其电枢绕组主要是与由永磁体产生的主磁通相对运动而感生电动势。通常而言，按每极每相槽数分类，可以分为整数槽和分数槽绕组；按槽内线圈边层数分类，有单层绕组和双层绕组；按绕组线圈的组成形式分类，可以分为硬绕组和散绕组。

1.1 整数槽与分数槽

每极每相槽数为整数时为整数槽绕组，而q不为整数时就是分数槽绕组。这两种绕组均可用槽电势相量图星形图分析。分数槽绕组的基本对称条件为：Q0/m=整数(其中Q/t、Q为定子槽数、t为极对数p与槽数Q的最大公约数)。其值为偶数时，线圈可接成单层和双层绕组，采用双层绕组时最大并联支路数amax为2t；其值为奇数时，一般采用双层绕组，其最大并联支路数为amax为t[2]。

1.2 单层绕组与双层绕组

单层绕组为每槽放一个绕组的线圈边，其中有同心式、等元件式和交叉链式等不同连接方式[3]，绕组由线圈个数和节距相等或不等的数个线圈构成。其优点有槽内无层间绝缘，槽利用率高；线圈数比双层绕组少一半，但同时因不能做成短距绕组，从而无法改善磁场波形。

双层绕组每槽分为上下两层，分别放置两个不同线圈的直线边。双层绕组的结构和尺寸均相同，连线整洁、美观，有利于散热和增加机械强度。同时可通过选择短距来改善电枢磁场波形，不足之处就是绝缘材料多，嵌线麻烦。

1.3 硬绕组与软绕组

散绕组由圆电磁线束包而成，其漆膜比较薄，耐冲击力差，很容易受到损伤，但结构简单、易绕制、端部短、用铜少、电阻和漏抗小。与其配套的半闭口槽槽口相对较小，有利于降低齿谐波幅值、均衡气隙磁场；硬绕组由数个独立的线圈构成，一般由扁铜线绕制而成，易保持一定的形状，根据实际情况分为多层结构，其机械性能、电性能、热性能和化学性能较散绕组均有不同程度的提高，是提高电机耐电压脉冲应力最好的绕组型式之一。但相对地，其端部长、用铜量多、铜耗大、电阻和漏抗大[4]。

2 分数槽绕组

对于直驱永磁电机，其极数较大，如果采用整数槽结构，一般按每极每相槽数q≥2设计，其定子槽数必然很大，定子冲片开槽和嵌线都很困难。通过综合对比，本方案采用双层短距分数槽绕组结构，分数槽绕组永磁电机不仅具有永磁同步电机特有的优点，还可以有效的削弱齿槽谐波，减弱齿槽转矩，减小电动势和电枢磁动势谐波分量幅值。其可以采用很少的槽数来实现与槽数很多的整数槽绕组的分布性能，同时采用分数槽在工艺上因为槽少而易于实现。

因分数槽绕组含有一系列次数与基波不成整数倍的谐波，其具有较大的谐波漏抗，但其在同步电抗中占得比例很小，只需注意与基波成奇数倍的谐波。分数槽绕组不能抵消的最低次数谐波为槽数和极数的最小公倍数次谐波[2]，对于本方案，其部分参数如表1所示，采用的是20极66槽结构，不能消除的最小谐波次数是660次，也既是齿谐波基波的10次谐波，而齿谐波基波以及2～9次谐波都已被抵消。另外值得注意的是分数槽绕组会产生幅值很高的磁动势谐波，每极每相槽数q分母不为2的时候会产生次谐波。因此，选取合理的极槽配合是直驱永磁电机设计的关键。

表1 直驱永磁电机部分参数

极对数p与槽数Q的最大公约数为t=2，其由p0=p/t=10/2=5对极下的Q0=Q/t=66/2=33个槽电动势相量组成一个完整的槽电动势星形图，如图1所示，共有2个重叠的基本星形，按槽号顺序列出的各槽所属相带见表2。

图1 槽电动势相量星形图

表2中一相绕组所在的槽数为有规则的数列循环，其数列为2111111111，由一个2和9个1组成。其值计算方式[2]为：(1)把每极每项槽数q表示为q=b+c/d，式中b为整数，c/d为不可约的分数；(2)一个循环数列共有d个数，其中c个为大数，大数为b+1，d-c个为小数，小数为b。

表2 分数槽绕组槽号与相带(因t=2，取槽数一半)

3 绕组参数计算及有限元分析

针对直驱永磁电机，对采用分数槽集中绕组和不同短距系数的双层短距分布式绕组进行了对比分析：计算了其绕组系数及各次谐波的含量；利用有限元法对比分析了永磁电机的空载线反电势和转矩波动；与采用斜槽结构的整数槽设计方案进行了方案对比。

3.1 分数槽绕组系数计算

3.1.1 分布系数和短距系数[2]

本方案采用分数槽绕组(q=b+c/d=N/D，其中D≠1，N和D没有公约数)，其基波和v谐波的分布系数为

(1)

(2)

基波和次谐波的短距系数为

(3)

(4)

式中，Z—定子槽数；y1—线圈节距。

kdp为绕组系数，是分布系数kd和短距系数kp的乘积。kdpv为对应于次谐波的绕组系数

kdpv=kdvkpv

(5)

3.1.2 永磁感应电势绕组系数计算

感应电势中的谐波对电机运行产生诸多不良影响，因此需要尽可能减少谐波含量和削弱谐波幅值。主要有采用短距线圈和非等元件绕组等方法[5]。双层绕组一般通过选用不同的节距来消除5次、7次等各次谐波，从而改善电动势和磁动势波形。

在定子槽数比较小时，节距按式y1=Z/2p选择(y1=Z/2p为向下取整，即取比Z/2p小的最大整数)，即线圈跨距接近极距，其基波绕组系数大[6]。通过表3也可看出，采用最大短距节距(即y1=3)时其基波绕组系数最大；采用分数槽集中绕组(即y1=1)时，其电枢反应磁动势谐波含量很高，但5、7次谐波含量最小。

表3 采用不同节距时绕组谐波系数

3.2 有限元分析

为了得到永磁电机准确的性能参数，需要对电机磁场进行数值计算与分析。而磁场数值方法有有限元法、有限差分法、边界单元法等，因有限元法特别适合边界形状复杂、材料存在非线性等磁场问题，其应用最为广泛[1]。

3.2.1 不同短距系数的分数槽方案对比

利用有限元法对采用不同短距系数的分数槽绕组直驱永磁电机，分别从空载反电势和转矩波动两个方面进行了对比分析。

(1)空载线反电动势

空载反电动势是永磁电机一个非常重要的性能参数，对电机的功率因数影响很大。其不仅决定永磁电机所处是增磁还是去磁状态，并对电机的瞬态和静态性能有很大的影响[7]。

对于直驱永磁电机，电机采用Y接，所以3及3的倍数次谐波空载线感应电动势为零。采用不同节距时，其谐波含量见表4。

图2 采用不同节距时线反电动势波形及谐波分布

(2)转矩波动

直驱永磁电动机运行时，一个很重要的性能指标就是转矩波动，通常转矩波动由上下波动值对其平均值的百分数表示，其定义公式为[2]

式中，ΔT—转矩波动；Tmax—最大转矩；Tmin—最小转矩。其对比分析见表5，可以看出，当y1=1其转矩波动最大，y1=2转矩波动最小，但三种方式均<5%。

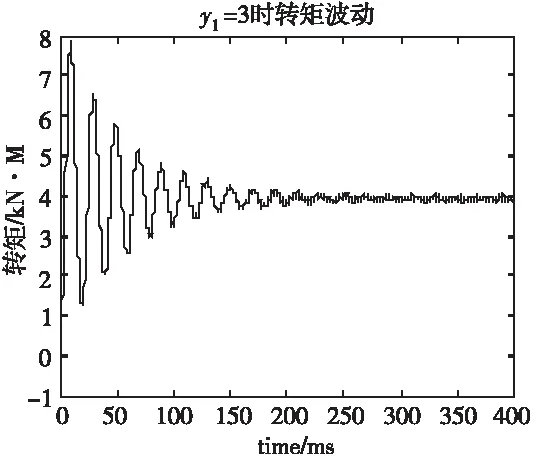
图3 采用不同节距时负载转矩波动

表5 采用不同节距时线反电动势谐波含量

3.2.2 与整数槽斜槽方案的对比

整数槽方案与采用分数槽不同之处在于其每极每相槽数为整数，为了削弱齿槽转矩而采用了定子斜槽结构，其对比方案见表6。同时从空载气隙磁密、空载反电势、齿槽转矩和转矩波动等方面对比分析了分数槽与整数槽斜槽结构的优劣。

表6 分数槽与整数槽部分方案对比

(1)空载气隙磁密

直驱永磁电机需要正弦波分布的空载相反电动势，如果气隙磁密分布均匀，则永磁电机可以得到正弦性良好的空载相反电动势，相反，则进一步影响电机的运行性能。

采用整数槽时其气隙磁密谐波含量远高于采用分数槽绕组结构时的谐波总含量见表7。

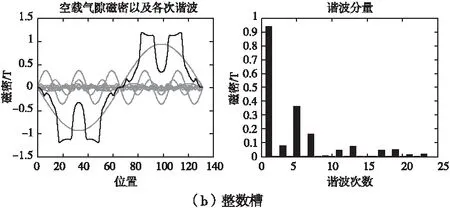
图4 空载气隙磁密波形及谐波分布

表7 空载气隙磁密各次谐波幅值及百分比

(2)空载反电势

对于直驱永磁电机，低速平稳性是一个很重要的指标，而影响其性能的主要因素为永磁电机的脉动转矩，包括纹波转矩和齿槽转矩[1]。其纹波转矩就是由电动势或电流非正弦引起的。因此，当电机处于空载时，对其反电势进行了对比分析，结果见表8所示。可以看出，分数槽优于整数槽结构。

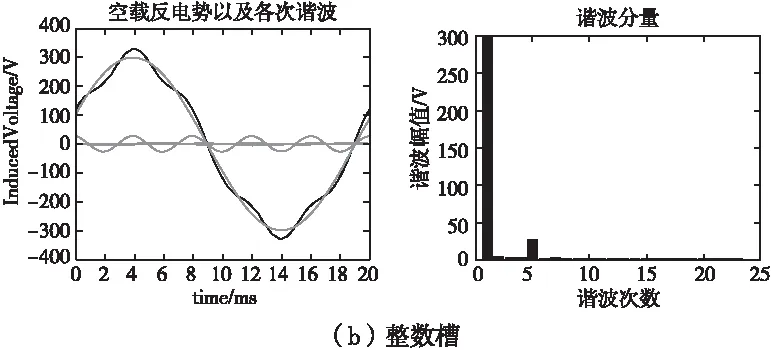
图5 空载相反电势波形及各次谐波分布

表8 分数槽与整数槽相反电动势谐波含量(%)

(3)齿槽转矩

由图6可知，分数槽齿槽转矩波动最大值为18 N·m，整数槽斜槽后其波动最大值为80 N·m，相差4.5倍，可见，分数槽具有明显的优势。

图6 齿槽转矩波形

(4)转矩波动

电机负载时，其转矩波动如图7所示。表9中结果显示，采用分数槽结构较整数槽时减少了6.67%的转矩波动。

图7 负载转矩波动

表9 转矩波动数值对比

4 样机试制

图8为现场嵌线时线圈成型图和总装完成后送往试验的图片，可以观测出铁心线圈整洁、紧凑。同时，随着试验的通过，最终验证了本方案选择的合理性。

图8 铁心线圈及直驱永磁电机

5 结语

通过选取合适的分数槽双层短距绕组，有效的削弱了永磁直驱电机的齿谐波和齿槽转矩，降低了电动势和电枢反应磁动势谐波分量幅值。通过分析采用不同短距系数分数槽绕组的优劣，与整数槽斜槽结构的对比，又同时从工艺角度出发，验证了直驱永磁电机极槽配合选取的合理性。

尽管分数槽集中绕组和整数槽分布绕组应用广泛，但需要对应一定的极槽配合：对于每极每相槽数为真分数(即极槽数相近配合)的时候，利于采用分数槽集中绕组；对于q为假分数的时候，需要根据实际情况对比选择合适的方案。