基于大型涵洞安全评估研究

(大连市普兰店区河道管理处，辽宁 大连 116200)

20世纪60年代为我国水工建筑物涵洞修建的主要时期，经过长期服役和运行，涵洞大多出现老化、失修、功能衰退等现象，不仅严重威胁着人民生命财产安全，而且严重影响水利工程效益的发挥。在涵洞工程安全评价方面我国众多学者已开展了大量的研究，如刘柏青等[1]在分析了灌区建筑物老化评价标准和指标的基础上对涵洞安全性态进行评估，然而以灌区建筑物指标方法进行涵洞的相关分析其研究理论和深度仍有待提升；赵立庭等[2]对京密引水渠沿线的水工建筑物利用钢筋锈蚀、碳化、施工缺陷、渗漏和裂缝等指标进行了定性的安全评价，并给出了引起涵洞病害的主要因素；然而，因所选取的影响因素不足仍存在主观随意性判断的弊端。当前，综合评价理论不够科学、无法合理量化评估指标以及评价指标体系不完善仍为涵洞安全评估存在的主要问题[3-4]。近年来，在水质安全、坝体变形、围岩稳定性、大坝工作形态、方案优选等多属性决策问题评判中采用最多的为可拓学理论和物元分析理论，该理论可对研究对象进行量与质的综合判断。由于涵洞工作条件以及结构型式复杂造成影响工作形态的因素较多，各种不确定性因素随着涵洞运行时间的推移而越来越多。据此，本文结合各主要影响因素，基于系统工程的方法和理论建立了涵洞工作形态评估物元系统，并在此基础上构建了模糊可拓模型，进而对各指标的重要性程度和特征值进行了合理量化，对涵洞的安全状态利用模糊可拓模型实现了动态评价。

1 大型涵洞安全评估物元系统

1.1 工作性态信息物元

描述事物的基本要素即为信息物元，它是进行涵洞安全评估的基本单元和前提条件。考虑到影响涵洞工作性态的影响因素较多，因此对于n维涵洞工作性态的物元R可采用下式进行表征：

(1)

式中N——评价对象，即事物的集合体或单个事物；

c、v——评价指标即事物特征和对应于评价指标的量值；

R——涵洞评估分物元，可反映第i个评估指标对涵洞工作性态的特征描述。

1.2 安全评估信息物元系统

结合物元分析理论基本内涵和特征，一个信息物元即可代表影响涵洞安全的每个要素，因此，应尽可能地考虑主要信息物元并进行整体性和独立性分析，构建多层梯阶结构信息物元系统并进行涵洞安全评估[5](见表1)。结合物元的发散性特征其第Ⅰ级物元即为涵洞安全直属特征；并且第Ⅱ级物元可反映第Ⅰ级物元特征，以此类推，上级物元特征可通过下级物元来反映和体现。

表1 涵洞安全评估信息物元系统

2 构建涵洞安全评估模糊可拓模型

2.1 评价指标集

结合待评价对象的实际状况和相关数据资料可将待评价对象N的涵洞安全评估等级划分为Ⅰ～Ⅳ个等级，各等级所对应的评语分别为正常、轻微异常、异常和险情，因此所构建的等级集合为N={N1,N2,N3,N4}。

2.2 评估经典域、节域

经典域物元R0可表示为

(2)

式中R0j——涵洞安全评估等级，j=1,2,3,4；

cj——物元评价等级；

N0j——所对应的特征值；

[a0j,b0j]——关于V0j在评估等级N0j所对应于特征值cj的取值范围。

因此，可采用下述公式代表节域物元Rp：

(3)

式中Np——涵洞安全评估等级全体；

[ap,bp]——关于Vp在评估等级Np所对应于特征值cj的取值范围。

2.3 待评价模糊物元

式(1)待评物元的量值vi在实际评估时具有一定的模糊性，因此该物元为模糊量值，也可称为模糊物元。在进行涵洞安全评价时各评价指标往往具有一定的模糊性，如对排水和防渗设施的倾斜、结构裂缝、完整性、电气设备、施工质量等特征均无法采用直接数值对其进行度量，其常用的表征方法为统计学方法或专家打分法并给出相应的模糊量值；虽然可通过计算手段或设计资料对其他各定量特征指标如配筋、地基承载力、渗透坡降、抗滑稳定、保护层厚度等进行获取，然而其评价等级的划分仍具有模糊性[6]。考虑到定量和定性指标取值范围、单位度量存在的差异性，不同指标之间无法直接进行对比分析，据此在评价前为使各指标具有可比性需对指标进行无量纲化处理，无量纲化处理按下述公式进行：

(4)

式中R、G——某项指标实测值和某指标专家给出的临界值或复核计算值。

2.4 确定综合权重

熵是信息论中系统无序性的度量指标，对各指标的熵权结合指标变异程度可利用熵法进行计算。各特征指标项决策者提供的有效信息量的大小可通过熵权计算结果进行反映和表征，某项特征的熵值越小则其熵权越大，其无序度就越低，所包含的信息量也越大。熵权法计算过程为假定待评价方案个数为n，各方案中有m个要素指标，则构建的指标特征矩阵为X=(xij)m×n(i=1,2,…,m;j=1,2,…,n)。然后构造判断矩阵并进行标准化归一处理，求得方案中第i个评价指标的熵权Xi，其表达式如下：

(5)

层次分析法是在详细分析了各作用影响因素、内在作用关系以及决策问题本质的基础之上，对定性和定量信息指标利用层次结构模型进行数学化处理，可简单、有效地解决无结构特性多准则复杂决策问题[7]。其计算步骤和方法如下：

a.建立结构体系。其中目标层仅仅含有一个元素，它是反映决策分析的总的目标；准则层和约束层分别为评价目标的子目标、特征、要素和实现目标的可行性方案、措施；而指标层则为涵洞安全评价详细的影响要素和参数指标。

b.依据准则构建判别矩阵。假设有m个决策方案或元素，利用1～9标度法对两两指标进行对比分析，根据某准则条件下各个目标的优先权重可构建一个m阶判别矩阵A=(aij)m×m。假定决策者可对aij(i,j,k=1,2,…,m)进行准确估计，可有aij=1/aji,aij=aikakj,ajj=1，利用判别矩阵可对各因素ω1,ω2,…,ωn在A条件下的相对排序权重进行求解(见表2)。

表2 判断矩阵取值范围

c.采用自上而下的逐层排序法对相同层次的各元素对最高层次的重要性权重向量进行计算；梯级结构中k-1层次上的nk-1个元素相对于总目标的权重向量为ω(k-1)=[ω1(k-1),ω2(k-1),…,ωn(k-1)(k-1)]T，其他各层次以此类推，最终可求得各层次相对于总目标和上一层次的权重向量。

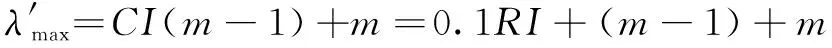
考虑到不同评价指标对评价结果的重要程度不同，对于较为重要的参数特征应赋予较高的权重。但是，熵权法计算权重往往以专家经验信息和决策者的主观判断为依据进行权重赋分，因此权重值具有较大的随意性且受专家主观偏好的影响较大；而层次分析法即客观赋权法往往是对各指标权重按照其所反映的客观信息进行反映，对于重要指标权重出现较大偏差的现象时有发生。据此，陈家良等[8]融合了主客观权重的优点给出了基于博弈论的组合权重法，其本质是对评价指标权重最优值进行求解。

假如对各项指标利用L种方法进行赋权，因此可获得L组权重向量，表达式如下：

uk=(uk1,uk2,…,uk16)

(6)

对上述权重进行任意线性组合有

(7)

对指标权重进行最优化求解即利用博弈论集结模型进行线性组合最优系数ak的求解，结合矩阵的微分性质，所满足的一阶最优化导数条件如下：

(8)

利用上述公式可求得ak，然后将其按如下公式进行归一化处理：

(9)

最后将经归一化处理后的最优组合系数带入式(10)可求得评价指标的综合最优权重W。

2.5 计算关联度

以Kj(vj)代表j标准等级下评价对象N的第i个特征关联度，按下述公式进行计算：

Kj(vj)=ρ(vi,v0ji)/[ρ(vi,vpi)-ρ(vi,v0ji)]

(10)

式中ρ(vi,v0ji)、ρ(vi,vpi)——点到经典域的距离和点到节域的距离。

利用关联度Kj(vj)从基层特征值逐层向相邻上层进行计算，公式如下：

Kj(N)=WKj(vj),j=1,2,3,4

(11)

式中W——评价对象整体权重矩阵，可通过各层权重叠加获取；

Kj(vj)——基层特征指标关联度矩阵。

2.6 评定等级

按照最大关联度准则K*=max{K1(N),K2(N),K3(N),K4(N)}对评价结果进行判定，根据等级判定结果可对不同涵洞安全现状和工作性态动态变化进行更深一步的分析。

3 实例应用

辽宁省大连市普兰店区碧流河流域穿堤涵洞始建于1980年，主要是以防洪排涝为主要功能的大型涵洞，堤顶高程和堤高分别为25.40m和6m。单孔箱涵设计流量为12m3/s，长宽均为3m，涵长为65m；启闭机为手摇单螺杆式，其迎坡面闸门和进口闸门分别为平面滑动式和钢筋混凝土式，底板高程12.0m。该箱涵在加固处理时更换了伸缩缝上水橡皮及其附件，并对其进行浇筑混凝土覆盖保护，同时在进水池底板增设反滤层，目前因服役运行时间较长，维护检修相对滞后等原因造成该涵洞处于老化、病害状态。

结合涵洞安全评估信息物元系统可知，影响涵洞安全的特征指标共有28个，首先按照无量纲化处理公式对定量、定性指标进行处理，使各指标值取值范围为0～1。各指标安全评估等级标准见表3。

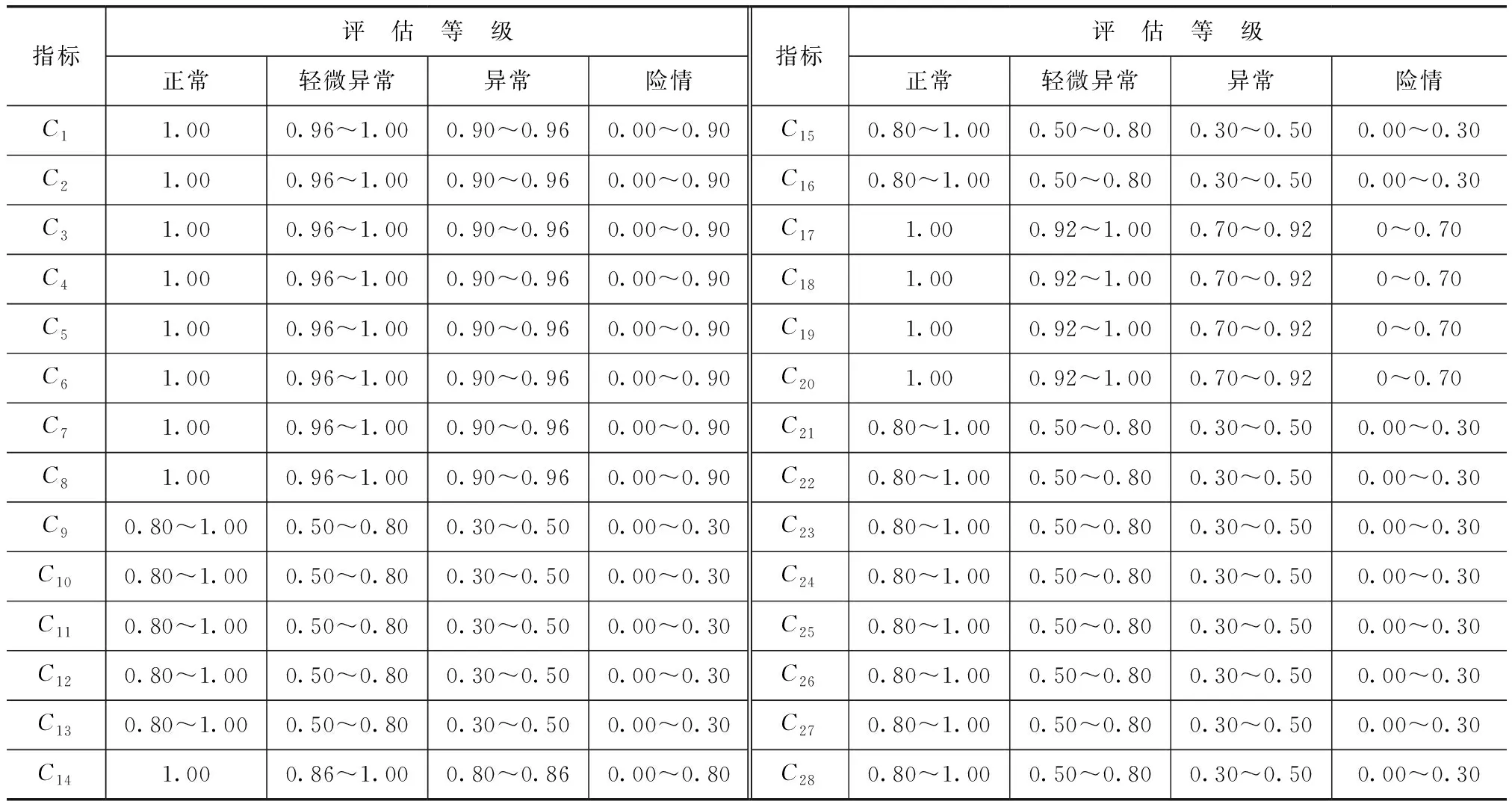
表3 涵洞安全评估指标等级标准

利用上述结果按照文中所述方法对各指标等级的经典物元和待评价模糊物元进行求解，各评价指标的组合权重计算结果见表4。

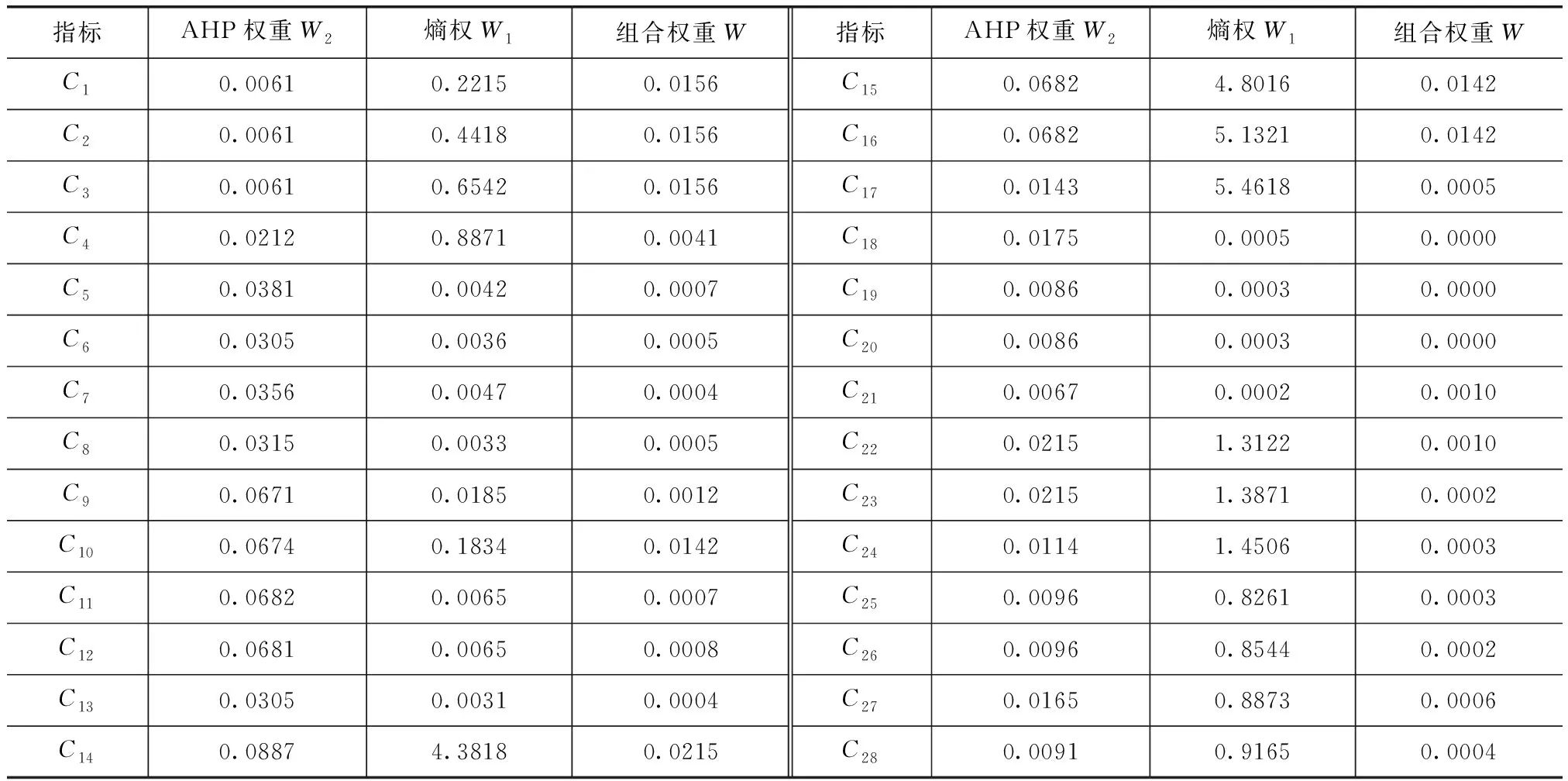
表4 各评价指标组合权重结果

利用关联度计算公式求得K*=max{-0.7518,-0.4235,-0.4165,2.5173}，并按照最大隶属度原则最终可判定该大型涵洞的安全性态处于第4等级标准，即该涵洞为病险等级，应尽快拆除并重新修建。经现场巡查发现，该涵洞在伸缩缝和底板处均出现拉裂和不均匀沉陷趋势，结构整体稳定性较差；启闭机台的渗流径不足且堤身出现严重渗漏现象，已不能满足安全使用要求；金属结构和闸门锈蚀和病害十分严重。因此，本文所采用的评价模型评价结果能够较好地反映该涵洞安全性态实际状况，具有良好的适用性与可靠性。

4 结 论

a.利用物元模型并结合系统工程理论对特征值、评价指标以及评价对象实现了统一联合，结合层次分析和熵权理论建立了基于模糊物元的多指标、多层次评价模型并实现了涵洞整体安全性态量与质的综合评价。

b.按照最大隶属度原则最终可判定该大型涵洞的安全性态处于第4等级标准，即该涵洞为病险等级，应尽快拆除并重新修建。现场调查和巡视发现该涵洞处于严重的病害状态。因此，本文所采用的评价模型评价结果能够较好地反映该涵洞安全性态实际状况，具有良好的适用性与可靠性。