超奇异椭圆曲线标量乘算法改进

徐雪莲

（上海海事大学信息工程学院，上海 201306）

0 引言

量子计算机（Quantum Computer），是一种全新的基于量子理论的计算机，遵循量子力学规律进行高速数学和逻辑运算、存储及处理量子信息的物理装置。在后量子密码学的前景中，许多已有方法将被淘汰，广泛使用的RSA系统将会过时。基于离散对数问题的椭圆曲线变量对量子分析不起作用，因此依赖于离散对数问题的任何机制都将变得很脆弱。目前，基于椭圆曲线的快速安全标量乘算法已经提出了很多，例如，椭圆曲线Montgomery型高效标量乘算法[11]，利用多基链计算椭圆曲线标量乘[12]等。然而，由于超奇异椭圆曲线易受MOV、FR攻击，此时离散对数问题会约减到一般有限域上的离散对数问题，因此，超奇异椭圆曲线曲线上的的快速标量乘算法没有很多的研究。文献[1]回顾了超奇异同源密码交换算法（SIDH），这种类型的密钥交换方案提供了前瞻性保密，量子系统的任何攻击仍然需要指数级别的时间。构造这样的密钥系统需要超奇异椭圆曲线以及他们的同源曲线。使用这种方案有很多优点，因为超奇异密钥系统依赖于常用椭圆曲线密钥系统实现中使用的许多相同的原语，因此现有系统可以非常方便的进行升级。另外，由于不受任何已知的专利的约束，可以对研究界保持自由和开放。超奇异椭圆曲线上的运算公式和标量乘计算方法也在不断地发展和改进，与椭圆曲线密码体制相比,超奇异椭圆曲线密码体制在量子计算机发展的大趋势与量子攻击的前提下具有更高的安全性。另外，像已建立的椭圆曲线系统一样，超奇异同源密码交换与已建立的ECCDH方案相比，提供了类似的密钥大小和计算效率。本文将在以下的内容中概述必要的数学概念，然后将椭圆曲线中的快速标量乘算法推广到超奇异椭圆曲线中，使用有符号滑动窗口的方法对密钥k进行编码，改进超奇异椭圆曲线下的标量乘算法。此外，提出使用额外寄存器的改进方法，安全快速的对编码k进行扫描。利用Frobenius自同态映射取代NAF算法中的倍增运算，并从硬件的角度考虑，并行的实施标量乘，使其具有能够快速运算并能够抵御能量分析攻击的性质。研究表明，在使用椭圆曲线时,长度为160bits的操作数与1024bits长度的RSA密码体制具有相同的安全性。因此，在满足我们的安全需求的情况下，推荐在超奇异椭圆曲线上建立的群的阶大小为2160，讨论特征为2的超奇异椭圆曲线上的运算，这样即可满足要求。

1 数学概念

1.1 椭圆曲线

定义：椭圆曲线（Elliptic Curve）是指代数闭包F上亏格等于1的一条光滑代数曲线。一般讲，由韦尔斯特拉（Weierstrass）方程：

确定的所有点的集合，外加一个无穷远点ο，称为椭圆曲线，参数a,b,c,d,e是满足一定条件的实数[3]。

（1）ο为加法单位元，即对椭圆曲线上任意一点p，有 p+ο=p;ο+p=p。

（2）p=(x,y)是椭圆曲线上的一点，那么它的加法逆元为 ρ=( )

x,-y，因为两点的连线可以延伸到无穷远处，得到无穷远点ο，所以 p,ρ,ο三点共线。

（3）设P和Q是椭圆曲线上坐标不同的两个点，P+Q的定义物理描述如下：画一条通过P、Q的直线与椭圆曲线交于 R'，交点唯一。由P+Q+R'=ο得P+Q=-R'。

（4）设P和Q是椭圆曲线上坐标相同的两个点，那么两点相加可以定义为点的倍数：在P点做椭圆曲线的一条切线，设切线与椭圆曲线交于R'，定义2P=P+P=-R'=R。

加法满足正常的加法性质，一条椭圆曲线上的一点P被一个整数k相乘则被定义为k个P相加。（5）由Hass定理[3]可知：

1.2 超奇异椭圆曲线

定义：满足以下条件之一的椭圆曲线称为超奇异椭圆曲线，其中P为椭圆曲线的特征，t为椭圆曲线的迹[2]。

（1）p|t，E的迹t能够被Fq的特征P所整除；

（2）p=2,3时，j(E)=0；p≥5，t=0；

例如，y2=x3+ax+b的 j不变量为 j(E)=1728∗4a3/(4a3+27b2)，当其值为0时，椭圆曲线为超奇异椭圆曲线。超奇异椭圆曲线对比普通椭圆曲线，常规椭圆曲线允许次指数量子攻击，而且在使用同源曲线的情况下，常规椭圆曲线速度很慢。

1.3 Frobenius映射

同源是一个重要的有理代数映射φ：两个椭圆曲线之间的E1→E2，使得对于所有E1上的几何点P,Q该映射也是一个群组同态，因为群组操作（加法/乘法）被保留并映射回同一组中的点。形成这样一个同态的两个椭圆曲线必须具有相同的点数。存在多项式时间算法用于对这些点进行计数。如果E是椭圆曲线，则[m]E是同源。一般情况下，基于有限域的椭圆曲线除了常数同态还有其他同态的。如果E：y2+cy=x3+ax+b是在特征p的有限域Fq上定义的椭圆曲线，Frobinus映射 E→E(P),(x,y)p→(xp,yp)是一种非常数同态。我们称椭圆曲线E具有复乘的属性，如果椭圆曲线的自同态中除了常数同态还有其他的同态类型时。

定义：令 a∈{0,1},Ea(F2m)在代数闭域上的Frobenius映射是：

γ：Ea(F2m)→Ea(F2m

),γ(∞)= ∞,γ(x,y)=(x2,y2)

γ满足方程 γ2-tγ+q=0，其中称为自同态 γ的迹，根据 Hass定理，并且#E(Fp)表示曲线上点的个数。二元域上的平方在多项式基下只需在元素之间插入零,然后约简，正则基下的所有运算只须循环移位.因此计算任何二元域元素的Frobenius映射是很快的。

2 快速标量乘法

2.1 特征为2的超奇异椭圆曲线

对于b∈{0 ,1}，m是与6互素的一个整数，选择MOV安全指数为4的椭圆曲线：

满足方程γ2-2(- 1)aγ+2=0。曲线E上的两个点。按照1.1中椭圆曲线的群运算法则定义，-ο=ο，-P1=(x1,-y1)，P+ο=ο+P=P可以得到：

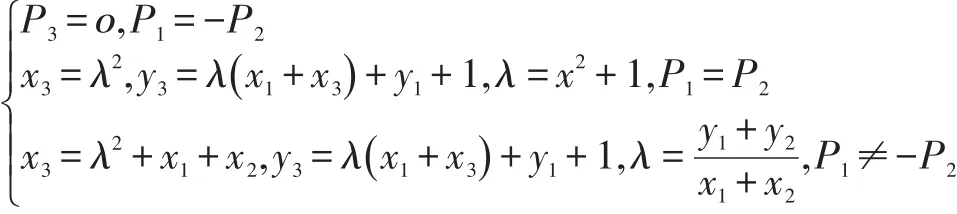
2.2 快速标量乘算法实现过程

算法1 NAF的编码方式及算法描述[10]

（2）当m＞0：

②令m←m-u；

③将u添加到S中；

④令m←m/2。

（3）输出NAF编码方式。

算法2计算KP

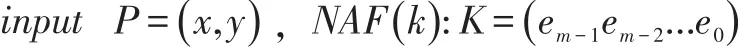
Q←P

for i=m-2 down to 0 do

Q←2Q+eiP

Output Q

由2.1超奇异椭圆曲线公式可得：2P=(x4+1,x4+y4)，成立，考虑使用映射：υ：(x ,y) →(x+1,x+y)；ο→ο。利用Frobenius自同态和υ自同态，得到一种可以简单计算的自同态：λ：(x,y)→(x4+1,x4+y4)，也就是 λ(P)=υ(φ2(P))。由于自同态的运算量与域中的计算量相比可以忽略不计，因此，上述算法二中的2Q步骤可以用自同态来代替。使用自同态快速算法的运算量仅仅为1/3n,运算效率提高75%[5]。

2.3 改进的快速标量乘算法

（1）有符号滑动窗口编码方式

滑动窗口编码可根据编码方式的不同分为无符号滑动窗口算法和有符号滑动窗口算法，具体指用一个宽度为w（一般w≥2）的窗口对标量k重新编码。接下来主要研究采用有符号滑动窗口大小为3的算法，并且以4位为窗口长度将k的二进制序列进行分组，当窗口的值为负数时，窗口的值用补码表示并产生一个进位。例如：k=101111000110000101001110转换后变为k=03000-1000030000005000070。

算法3：

Input： 整数 k

Output：k的有符号滑动窗口编码方式

For j from 0 up to n-1 do：

由2.1超奇异椭圆曲线公式可得：3p、5p、7p的表达式，分别预计算出对应的倍点值。

预计算步骤：

①P1=P,P2=[2] P;

② i从1到2w-1-1计算P2i+1=P2i-1+P2;

③ i从1到2w-1-1置P2i+1=-P2i+1;

也可使用Frobenius自同态方法组合简单的自同态计算出2p、4p、8p的运算公式，进而得出预计算表Pkj={p,3p,5p,7p…}，仅提供思路。由于，点之间相减的运算时间短于点加的时间。由此，我们可以得到：

①p1=p,p2=[]2 p;

②3p=4p-p;

③5p=8p-3p;

④7p=8p-p;

由超奇异椭圆曲线的的公式可得4p=(x16,1+y16)

主循环：扫描k时，由于窗口大小为4，选择每4位计算一次。额外增加一个寄存器用m表示，初始值为4，用于记载每四位中0的个数。扫描次数可减少为一半，当扫描到非0位时根据m的大小进行相应次数的倍增，因此提高了运算速度。

当j＞=0时执行：

① d000：Q=( )Q+Pkj 16 j=j-m,m=4;

②0d00：ki=0,Q=Q,j=j-1,m=m-1;

Q=( )

2Q+Pkj 8,j=j-m,m=4;

③00d0：ki=0,Q=Q,j=j-1,m=m-1;

Q=( )

4Q+Pkj 4,j=j-m,m=4;

④000d：ki=0,Q=Q,j=j-1,m=m-1;

Q=( )

8Q+Pkj 2,j=j-m,m=4;

⑤0000：ki=0,Q=Q,j=j-1,m=m-1;

Q=16Q,j=j-m,m=4;

其中d表示不为0的ki，j表示位移变量,Q=kp,初始值为O，其中4Q、8Q、16Q使用Frobenius映射代替点的倍乘。

3 抗功耗分析攻击及防御的方案

简单能量分析。SPA利用算法执行期间基于正在处理数据的指令进行攻击。显然，二进制算法具有由整数ki调节的分支指令，因此它能够揭示出秘密位ki。为了抵抗SPA，应该消除任意的标量乘算法中的分支指令。固定程序方法删除由秘密指数d和基于窗口的方法调节的任何分支。算法3中，当ki=0时，采用Q=Q的方法，使攻击者无法识别出ki位的值，因此算法3能够抵抗简单能量攻击。

DPA使用能量消耗和特定密钥位之间的相关性，攻击者通过大量的数据分析能量消耗得到ki位取值。为了抵抗DPA，在每次新的点倍执行时都应该改变功耗。主要有3种对策，随机投影坐标法（RPC）、随机曲线法（RC）和指数分解法（ES）。RPC使用雅可比或投影坐标来分别将P(x,y)随机化为(r2x,r3y,r)或

对m，n进行窗口为w的有符号滑动窗口法重新编码，m、n的长度相同，调用算法3分别计算mp、np。使用随机化密钥r的方式能够有效的抵抗DPA。由于加密时使用的k是随机变化的，攻击者无法形成有效的能量曲线，无法从大量的数据中得到密钥的有效信息，从而阻止了DPA攻击。随机化密钥后每次r的取值不同，产生的编码也不同，每次标量乘计算中标量的值与密钥无直接关系。倍增运算由于采用Frobinus映射，也使得攻击者无法判断密钥位。因此，采用随机掩码的方式计算标量乘可以抵抗RPA、ZPA攻击。从硬件的角度来说，可以采取并行的方式同时计算mp和np两个部分，运算效率得到进一步的提高。

4 效率分析与比较

比较算法3与已有的的二进制算法，NAF算法，算法3从多个方面降低了计算的复杂度，提高了运算效率。具体从整数k的表示方法、预计算表、k的编码扫描累加赋值阶段，硬件方面。k的有符号滑动窗口表示方法使得非0位个数减少，也就使得标量乘中点加的次数减少。传统算法中需要L次倍点计算及不超过L+2次的点加计算。表1[9]列出不同坐标系下需要的计算复杂度。

在Chudnovsky Jacobian坐标下，总的计算量最小，整体的计算量约为：献中[6]证明采用Affine和Jacobian混合坐标系计算算法中2wR+S的计算量最小为(4 w+3) S+(4w+9)M。利用超奇异椭圆曲线自同态映射进行倍点运算的效率比较传统的倍点运算效率提高了75%，所以提高整体的计算量集中在减少点加运算次数上。文献[7]中证明长度为Lbit的二进制标量k采用滑动窗口进行编码后,非零位的平均个数为L/(w+2)，其中(w+2)为有符号滑动窗口编码方法中的平均窗口宽度。安全性分析中取得随机数时间及k的编码时间可以忽略不计。

表1 不同坐标系点加和倍点计算量

假设点加和点倍运算相同以及密钥长度为160bit，表2列出几种算法在假设前提下需要计算的点加量。比较本文算法与传统的二元法下的窗口算法、NAF算法的计算复杂性，具体从预计算和累加赋值两阶段进行比较。

表2 不同算法点加量

使用预计算表的方式使得标量乘过程中的点加运算可以查表获得。不使用同源映射的情况下，预计算需要进行2w-1-1次的点加计算以及一次倍点运算，然后主循环部分进行次计算，一次点加计算。所以整个运算量为预计算与主循环部分之和主循环部分用额外寄存器的方法统计窗口大小的扫描单位中0的个数，使k的扫描次数减少一半。结合寄存器m中的值对2Q进行m次映射。因此，整体上是的标量乘的运算效率提高了80%左右。据分析，当L取160时，w取3的时候效率最高。表3列出几种算法的计算量比较。

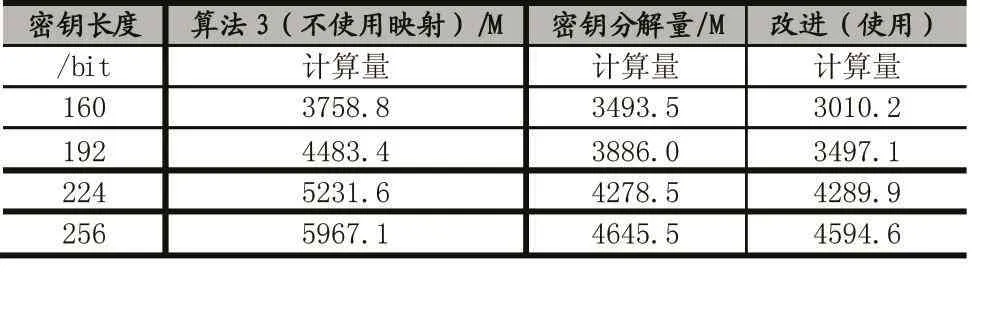
表3 计算量

5 结语

本文基于Frobenius映射给出了超奇异椭圆曲线上的一种改进算法，该算法使用有符号滑动窗口算法来减少标量乘计算中编码k的非0位出现的次数，同时使用了预计算表来提高累加赋值阶段的效率。由于改进算法采用额外的寄存器加快了0位的扫描速度，使用高效的Frobenius映射无须进行倍点运算，所以进一步提高了标量乘算法的效率。