基于因子分解机的推荐模型研究

饶 健

(三明学院信息工程学院，福建 三明 365004)

0 引言

随着互联网与通讯的发展与普及，网络传播渠道越来越受到一些商家和公司的青睐。而在互联网上，电子零售商和内容提供商给用户提供了巨大的产品选择空间。互联网公司拥有前所未有的机会来满足各种用户的需求，来提高用户的浏览体验[1]。其中，由于网络巨大的浏览空间，如何抓住用户的眼球，为消费者匹配最合适的产品是关键，这可以提高用户的满意度和忠诚度。在用户方面来说，由于网络上日益剧增的信息量，他们很难在众多的信息中找到最想要的数据。因此，越来越多的网站已经建立推荐模型，这种服务模式通过分析产品与用户之间的兴趣模式，如用户的历史数据、浏览、个性集群、评分等等，为用户自动过滤商品或排序商品，提供个性化的商品建议，以适应用户的需求，而不需要用户手动选择。好的个性化建议，蕴藏着巨大的商机，也可以添加另一个层面的用户体验。像亚马逊、淘宝和Netflix公司等电子商务网站，推荐模型已经成为网站的重要组成部分[2]。

除了电子商务网站以外，这种推荐模型还特别适用于娱乐产品，以及其他互联网领域，如电影、音乐和电视节目、新闻热点挖掘，以及社交网站和搜索引擎。在电影方面，很多客户都会看同一部电影，每个客户也都有可能看很多不同的电影。当客户愿意表明他们对特定电影的满意度时，就可以得到一个庞大的用户电影评分数据库。企业可以利用这些数据进行评估分析，针对性地推荐电影给特定的客户[3]。而在新闻、社交网络中，信息过载的问题也亟待解决。分析海量的文本数据以及现有的用户行为日志，挖掘出价值信息或不同用户的关注热点，提炼出关键词，然后将用户感兴趣的热点推荐给他进行浏览，可以极大地提高用户的浏览效率。

推荐模型的研究和实践从用户和内容提供商角度来看，都有非常重要的意义[4]，同时在商业上和用户本身的需求方面来看，也都有巨大的价值。从大数据的研究和挖掘方面来看，推荐模型的研究不仅可以实现数据的挖掘和知识的发现，也可以极大地拓展研究者的研究视角以及深度挖掘商业价值。

1 问题描述

在现实世界中，许多应用问题都会产生高度稀疏的(特征)数据，即特征向量x中几乎所有的分类都为0。这里，我们以一个电影评分系统为例，给出一个关于高度稀疏数据的实例。考虑电影评分系统中的数据，它的每条记录都包含了哪个用户u∈U在什么时候t∈R对哪部电影i∈I打了多少分(分值r∈{1，2，3，4，5})等信息。假定用户集U和电影集I分别为：U={Alice(A)，Bob(B)，Charlie(C)，…}，I={Star Trek(ST)，Notting Hill(NH)，Titanic(TI)，Star Wars(SW)，…}，那么观测到的数据集合S为：S={(A，SW，2010-4，1)，(A，TI，2010-1，5)，(B，ST，2009-8，5)，(B，SW，2009-5，4)，(C，SW，2009-12，5)，(C，TI，2009-9，1)}。

我们运用这个实例来进行预测电影的评分。在机器学习中，预测是最基本的任务，实际上预测就是一个估计函数：

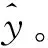
2 模型建立

对于这类不只与用户和商品有关的上下文问题，通常情况下，线性推荐模型的精确度太低。Factorization Machines(FM)模型[5]结合二阶支持向量机模型在推荐模型中的表现，本文可以建立以下非线性的特征向量相互作用模型方程：

(1)

式中w0和wi，wij为模型参数，这个方程有点像d=2的polynomialSVMs(K(x，z):=(+1)d)，然而，FM模型用矩阵和向量的思想对其进行了改进，对所有的特征分量x引入了辅助向量v，例如xi的辅助向量vi=(vi1，vi2，...vik)T∈Rk，i=1，2，...，n，k∈N+为超参数，并将w改写为：

(2)

于是函数可以进一步改写成:

(3)

式(3)便是FM模型在当交互为2(d=2)时的通式，其实它也可以推广到任意多阶。在这里以式(3)来分析结合上下文的FM的主要特点以及对比式(1)的优点。

3 目标优化函数

FM的模型建立之后，接下来在数据中通过机器学习得到这个模型。FM模型可以进行各种预测任务，如回归、分类和排名。在电影评分系统中，由于目标预测是一个评分值，便是一个回归任务。下面我们以回归和二分类任务为例来构造优化函数，进行算法学习。优化目标函数通常为一个整体的损失函数[6]。对于回归问题，损失函数可以取最小评分误差，即

(4)

对于二分类问题(标签y∈{+1，-1})，损失函数可以为hinge loss函数或者logit loss函数。

hinge loss函数：

(5)

logit loss函数：

(6)

此外，为了防止过拟合，我们通常会在优化目标函数中加入正则项。FM的最优化问题就变为：

(7)

这里用的正则项为L2正则，λ为参数的正则化系数。问题即找到最好的参数θ群，使式(5)的取值最小。θ群即为FM模型中的w0，w以及v。

4 实验与性能分析

推荐模型的开源数据并不多。MovieLens[3]是由美国明尼斯达大学计算机科学与工程学院的GroupLens项目组设计的较早的推荐模型，是一个非商业性质的、以科学研究为目的的实验性网站。他们提供了几个大小不一的基于电影评分系统的数据集，与我们上述说的电影评分案例数据类型基本相似。

Rendle等[7]提供了一个开源的FM模型的工具包：LibFM，在里面可以使用各种算法对FM模型进行训练。这个工具包经过拓展，已经可以用于C/C++、java、以及python等各语言中。我们将借用LibFM工具，进行不同学习算法之间，以及某些参数的大小选取在movielens这个数据上的精确度比较。首先对于随机梯度下降法的步长进行选择(迭代次数为1 000，k=4，λ=(0，0，0.1)，σ=0.1)。图1中，Y轴代表的是均方根误差(RMSE)。

图1 SGD中α的选取

与之对应的最小交替二乘法(迭代次数为1 000，k=4，λ=(0，0，0.1)，σ=0.1)的RMSE为：测试集：0.027，训练集1.202。马尔科夫蒙塔罗法(迭代次数为1 000，k=4，σ=0.1)的RMSE为：测试集：0.752 5，测试集：0.928 5。

从实验结果可以看到在训练集对函数拟合上，交替最小二乘法要明显优于随机梯度下降法。这是因为随机梯度下降法依赖于步长的选择，而且很容易陷入局部最优解。而马尔科夫蒙塔罗法由于采用自适应的方式，能有效地防止过拟合。速度方面，交替最小二乘法与随机梯度下降法速度相近，而马尔科夫蒙塔罗法比起前两种方法较慢一些。我们在马尔科夫蒙塔罗法上再分析k值的大小对结果的影响(迭代次数为1 000，σ=0.1)，图2中，Y轴代表的是均方根误差(RMSE)。

图2 MCMC中k的选择

从图2可以看出当k从2增长到16时，对于测试集的准确度基本上没有太大影响，而时间复杂度却大大提高，所以在模型中，一般我们选取k为4或者8。该数据测试的结果大部分依赖于具体的数据集(例如步长α的选择)，不过对于k值还有正则化系数的选择可以推广到一般情况。

5 结语

本文主要针对之前传统的推荐模型和FM模型进行了性能上的对比，通过选取具有典型代表的数据集进行了模型预测，验证了FM模型在加入新的特征因子之后对模型的精准度的提升以及因子分解模型对稀疏的矩阵仍然具有很好的学习能力，也表明了隐因子的抽取对于数据集能够有更好的描述以及对模型预测更为精准。