基于扰动观测器的光电跟踪平台滑模控制
朱海荣 ,焦子韵,冒建亮,李 奇,闫辰阳
(1.江苏工程职业技术学院 机电工程学院,南通 226007;2.南通大学 电气工程学院,南通 226019;3.东南大学 自动化学院,南京 210096)
安装于运动载体上的光电跟踪平台能隔离载体扰动、在惯性空间保持“稳定”,从而实现对目标的精确跟踪。光电跟踪平台在军事和民用领域有很大的应用前景,对其控制策略的研究很有理论意义和实际应用价值[1]。
对于光电跟踪平台来说,设计中对该类装置的稳定精度、响应速度等均提出了很高的要求。基于经典控制理论的方法在稳定回路控制中处于主导地位,如PI校正、滞后超前校正。为了改善系统性能,国内外研究者开展了先进控制方法的研究,取得了一定的研究成果[2-4]。由于现代控制策略实时性的问题使之大多只是停留在理论分析和仿真阶段,在装备中实用的尚不多见。
光电跟踪平台受到的干扰因素较多:由载体姿态变化引起的负载力矩变化;由结构强度和润滑条件限制带来的摩擦力矩;线缆约束、质量不平衡产生的附加干扰力矩以及轴系间耦合因素等[5]。由于上述非线性和不确定性因素的存在,很难建立光电跟踪平台精确的数学模型,在建模时只能做合理的近似处理,忽略对象中的参数误差、测量噪声、未建模动态和不确定的外部干扰等不确定性因素,由此设计的控制器,由于忽略了上述不确定因素可能引起控制品质的下降甚至不稳定。
滑模控制对系统参数变化和负载扰动不敏感,具有鲁棒性好、响应速度快及容易实现等优点,可以有效解决实际应用中存在的上述问题[6],对此设计了一种滑模控制策略用于光电跟踪平台。在常规滑模控制中,系统的大部分扰动都需要依靠滑模控制器来抑制,对于滑模控制器来说,需要保持较大的符号函数切换增益,这就导致了系统抖振较大[7]。为此我们引入扰动观测器,利用扰动观测器观测出系统的总扰动,并且在控制量中进行相应的补偿,这样就可以减小滑模控制器所需要的切换增益。通过光电跟踪平台实验表明所提出的基于扰动观测器的滑模控制减小了常规滑模控制器设计时存在的速度抖振,系统动静态性能得到了明显的改善,控制器的鲁棒性较好,达到了设计要求。
1 光电跟踪平台模型
图1为光电跟踪平台结构示意图。

图1 光电跟踪平台结构示意Fig.1 Schematic diagram of electro-optical tracking platform
忽略电机电枢电感的影响,成立如下通用关系式:
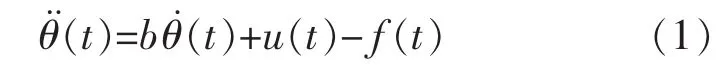
式中:θ(t)为光电跟踪平台视轴相对于载体基座的相对角位移(θ(t)=θl(t)-θb(t));u(t)为控制量;f(t)为系统建模误差和各种外部扰动总和;b为简化后的系数。
设位置参考信号为θr(t),定义误差及其导数分别为
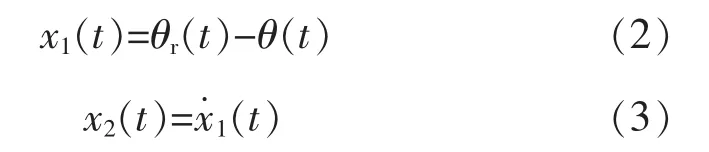
可以得到系统状态方程为
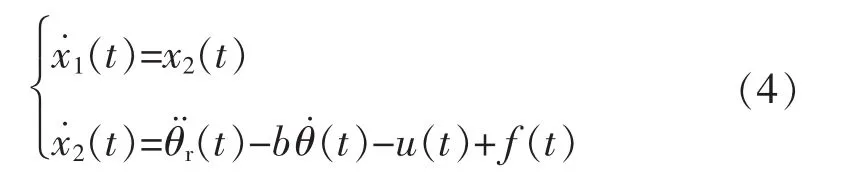
2 滑模控制器设计
滑模控制本质上是一类特殊的非线性控制,与其他控制的不同之处在于系统“结构不固定”,可以在动态过程中,根据系统当前状态不断变化,迫使系统沿预定“滑动模态”的状态轨迹运动。滑模控制方法实现简单,在工程领域得到了广泛应用[8],可以满足跟踪稳定系统实时性高的要求。
对于系统(4),我们按如下步骤设计滑模控制器:
1)确定切换函数
选取滑模开关函数S=cx1+x2
2)求滑模控制律
为使系统状态在有限时间内达到并保持在滑模面上,滑模控制律应满足SS˙<0。
确定函数切换控制的变结构控制方案:usmc=ueq+usw
其中ueq为滑模等效控制部分,usw为滑模切换控制部分。ueq为系统在S˙=0 和f(t)=0 时所需要的控制量, 根据滑模等效控制条件S˙=cx˙1+x˙2=0 求出等效控制ueq。
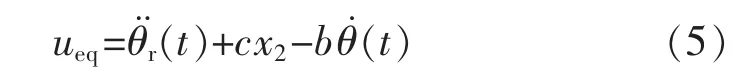
取usw(t)=k·sign(S),k为切换增益,sign(S)=为符号函数。
由此可得滑模控制器控制量为

下面证明常规滑模运动的存在性和可达性条件及滑动模态的稳定性。
假设 1:系统扰动f(t)有界,即满足
定理1:若式(4)所描述系统满足假设1,在式(6)所设计滑模控制器作用下,系统的误差能收敛于零。
证明:对于滑模控制律(6),当满足假设1时,有k-f(t)>0,则S≠0 时有以下关系成立:
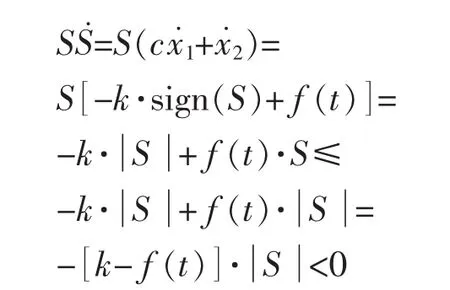
证毕。
切换增益k在补偿模型误差、抑制干扰中起到非常重要的作用。当系统处于初始状态开始向滑模面运动时,需要较大的k以减少达到时间,但是如果k取得过大,会给系统带来抖振;k取得过小,又会导致系统失去抗扰性,从而变成不稳定系统。在实际系统中,抖振会影响系统的动态性能,它有可能破坏系统滑动模态的运动条件,使系统出现超调,调节时间过长,甚至出现不稳定状态;抖振还会使系统的稳态性能变差,能耗增大,加速机械系统的磨损,或激发起系统固有振荡,使系统无法工作。
为了保证到达切换面的快速性同时减弱滑模控制的抖振,同时采用了如下2种方法:一是对滑模控制器的切换增益k进行优化设计,此处根据系统趋向滑模面的速度设计符号函数切换增益为为可调系数);二是采用扰动观测器观测出由系统模型参数变化等各种因素造成的总扰动,在控制量中进行相应的补偿,以减小滑模控制器所需要的切换增益k,下面分别进行变增益滑模控制和扰动观测器的设计。
切换控制部分设计如下:
由此可得变增益滑模控制器控制量为
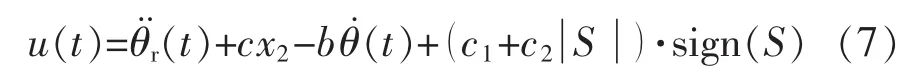
下面证明变增益滑模运动的存在性和可达性条件及滑动模态的稳定性。
假设 2:系统扰动f(t)有界,满足
定理2:若式(4)所描述系统满足假设2,在式(7)所设计滑模控制器作用下,系统的误差能收敛于零。
证明:对于变增益滑模控制律(7),当满足假设2 时,有c1-f(t)>0,则S≠0 时有以下关系成立:
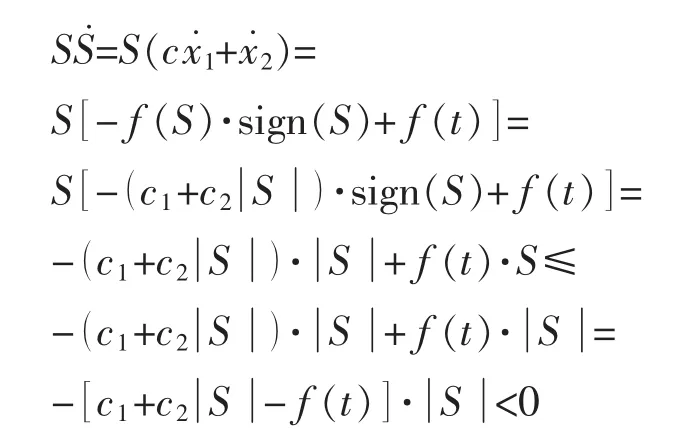
证毕。
结论:由式(7)得到的变增益滑模控制器保证了滑模的存在性和稳定性,即S≠0时有SS˙<0成立。由于采用了变增益函数f(S),c1可以取得比常规切换控制(usw=k·sign(S))中的k小,也能保证系统稳定,同时可保证趋近率速度随着距离切换面的远近而变化,相比常值切换控制策略有效地减小了抖振和过渡时间。同时,由假设2可知,当系统扰动f(t)很大时,c1相应要取较大的值,此时仍然会导致较强烈的抖振,影响系统性能。下面引入扰动观测器,作为滑模控制器的前馈对扰动进行补偿,以减小滑模控制器为抑制系统扰动所需的切换增益,进一步减小系统抖振。
3 扰动观测器设计
扰动观测器(DOB)的基本思想是把实际系统输出与参考模型输出的差异作为一个等效的干扰,DOB估计出这个等效干扰,并将其作为一个补偿信号前馈到控制输入端,以消除干扰对系统性能的影响[8]。这里的干扰定义为所有的外部干扰信号和由于实际对象和标称对象之间的差异引起的等效扰动,比如模型不确定性和参数摄动所引起的所有可能的信号。采用扰动观测器补偿的设计方法只需要很少的计算量,能够满足实时性的要求,并且不需要额外的传感器,是一种廉价的实现方法[9]。
扰动观测器(DOB)的基本结构如图2所示。

图2 扰动观测器结构Fig.2 Block diagram of disturbance observer
图中Gp(s)为实际对象模型,Gn(s)是系统参考模型,设Gn(s)和Gp(s)由乘性不确定性描述为,其中ΔM(s)为乘性摄动。Q(s)为一低通滤波器。分别为输入扰动、干扰观测值、前端控制器输出、总控制输入、测量噪声和系统输出[10]。由图2可得输出y的传递函数如下:
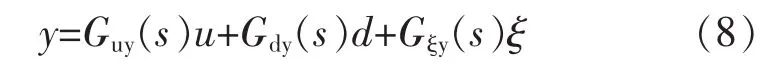
其中:

为了达到抑制低频噪声和高频测量噪声,要求在低频段,Q→1,使得Guy→0、Gdy→0,扰动观测器使实际模型与参考模型相似,具备很强的抗扰动性能,同时扰动观测的前馈会引入噪声;在高频段,Q→0,使得Gξy(s)→0,扰动观测器环相当于开环,没有前馈作用,因而不会由于加入扰动观测器而引入测量噪声。
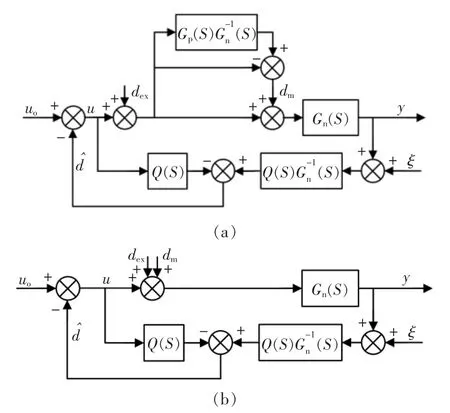
图3 扰动观测器等价结构Fig.3 Equivalent diagram of disturbance observer
考虑模型失配等效的内部扰动dm,得到系统等价结构,如图3(a)。经过变化后扰动观测器最终等价结构如图3(b)所示,总扰动包括内部扰动和外部扰动。为使系统可实现,要求使正则,即Q(s)的相对阶应不小于Gn(s)的相对阶。 对于光电跟踪平台来说,系统外部扰动和跟踪指令信号主要集中在低频段,而测量噪声主要分布在高频段。相对阶较低的Q(s)对数幅频特性曲线的高频段平缓,不利于抑制噪声,而相对阶较高的Q(s)不利于系统在谐振频率附近的鲁棒性,故Q(s)的设计应在干扰观测器的鲁棒稳定性和干扰抑制能力之间进行折中。
Q(s)设计如下,,式中为二项式系数,N为Q(s)的阶次,N-M为Q(s)的相对阶次,τ为Q(s)时间常数。 τ越小,扰动观测值收敛速度越快,系统抗干扰能力越强,抑制噪声能力越弱;τ越大,抑制噪声能力越强,但抗干扰能力下降。综合考虑选取τ为控制器采样周期的10倍。
基于扰动观补偿的滑模控制系统结构如图4所示。
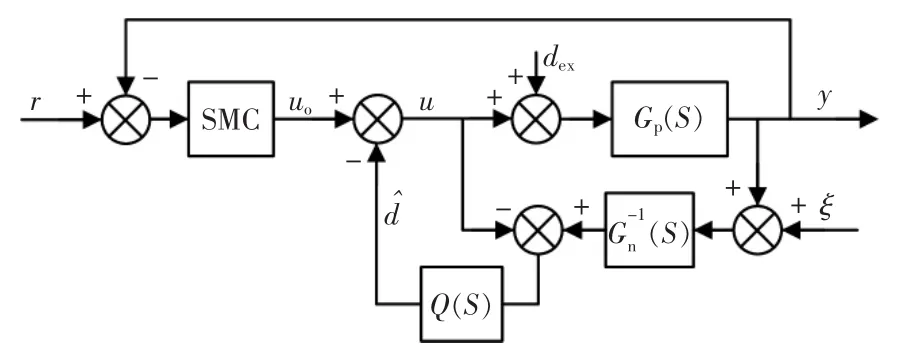
图4 基于扰动观测器的滑模控制结构Fig.4 Block diagram of SMC based on DOB
4 实验分析
在图5所示的某型号光电跟踪平台中,最外面两个框架为扰动平台,用于模拟载体扰动;内部两个框架为光电跟踪平台,由外方位框和内俯仰框构成,光电跟踪装置安装在俯仰框,用于目标识别并给出脱靶量信号。

图5 某型号光电跟踪平台实物Fig.5 Photo of an electro-optical tracking platform
采用Solid Edge V9对方位框进行建模后得到其转动惯量为0.31 kg·m2,根据上述指标,分别选用成都电机厂的分装式永磁式J130LYX05K型直流力矩电机作为动力装置,选用俄罗斯Fizoptika公司的VG941-3AM型光纤速率陀螺作为速度反馈装置。电机参数如下:连续堵转电压14 V,连续堵转电流5 A,连续堵转转矩5 N·m,峰值堵转电压27 V,峰值堵转电流10 A,峰值堵转转矩10 N·m,空载转速210 r/min,电气时间常数1.5 ms,电枢转动惯量0.006 kg·m2。光纤陀螺具体参数如下:测速范围±500°,启动时间 0.1 s,偏差重复性 0.003°/s,比例因子 6 mV/°/s,比例因子重复性(稳态)0.1%,比例因子稳定性(稳态)0.03%,比例因子变化(OTR)5%,角度随机游走 PSD0.0015 deg/s/sqrtHz,频率范围 0~500 Hz,振动 6g,20~2000 Hz,冲击加速度 90g。
选用TMS320F2812 DSP作为主控芯片,通过DSP运动控制模块所配置的各类输入/输出模块接口,接收速率陀螺信号、读取控制IO信号量、输出控制信号,伺服控制板如图6所示。

图6 光电跟踪平台伺服控制板Fig.6 Servo control board of an electro-optical tracking platform
在上述平台上展开实验研究,图7为横滚框给定正弦输入信号时,分别采用固定切换增益滑模控制(图7a)、变增益滑模控制(图7b)、带扰动观测器的变增益滑模控制时滑模控制器输出曲线(图7c)。从图7中可以看出,采用变增益滑模控制对抖振现象有一定的抑制作用,由于稳定平台受到的扰动因素较多,因而控制输出曲线依然存在小幅振动;引入扰动观测器以后,可以对系统所有的外部扰动和由系统模型参数变化带来的扰动进行补偿,使得系统在趋近滑模面时具有很小的切换增益,系统状态在收敛过程中更加平滑,输出曲线平稳,稳态精度更高。
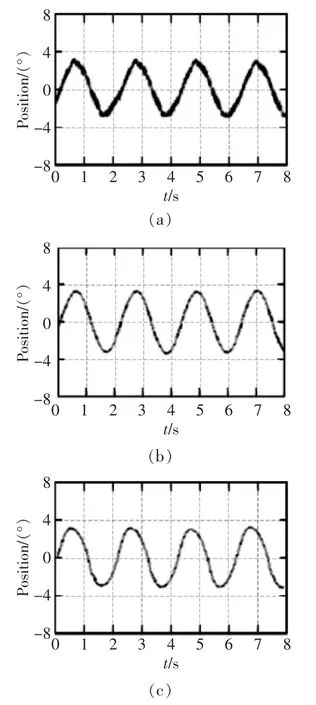
图7 滑模控制器输出曲线Fig.7 Output curve of sliding mode controller
5 结语
滑模控制具有响应快、对参数变化及外部干扰具有强鲁棒性和物理实现简单等优点,设计了光电跟踪平台滑模控制算法。经过实验对比,常值切换滑模控制会给系统带来较大抖振,满足不了现场需要;变增益切换滑模控制可以改善这方面的性能,但是当外部载体扰动很大时仍使系统存在一定抖振;考虑到扰动观测器结构简单,易于实现,设计了基于扰动观测器的变增益切换滑模控制,通过扰动观测器观测出各种扰动并进行补偿,从而减小滑模控制的切换增益,使系统抖振进一步减小。通过理论分析和实验验证了该复合控制算法的有效性性,取得了很好的控制效果。

