长耳鸮翼型气动及声学特性研究

张 康，杨爱玲，董云山，陈二云，戴 韧

（上海理工大学 能源与动力工程学院, 上海 200093）

流动效率、噪声是风机、水泵、风力机等叶轮机械的重要性能指标，高流动效率、低噪声的叶轮机械一直是研究人员和制造商努力追求的目标。然而，随着设计水平与控制技术的提高，许多目前比较常用的翼型流动及噪声性能优化方法已经遇到了瓶颈，在这种情形下，仿生技术成为一个十分重要的研究方向。

长耳鸮具有静音飞行的特点，这可能与其翼型有密切的关系。目前已有研究确定鸮翼噪声（散射噪声）与飞行速度的5次幂有关［1］，而鸮还能有效降低2 kHz以上的高频噪声。Graham［2］认为鸮类具有的天鹅绒般覆羽、锯齿状前缘和干涉状后缘是降噪的主要原因。鸮类飞行时，空气掠过其翅膀时的流动状态与结构是决定鸮升力大小的关键因素，因此，可以推断鸮类翅膀截面形状与鸮类气动以及其空气动力噪声有着内在联系。Kondo等［3］对鸮翅膀40%截面处的鸮翼绕流流场进行数值模拟的结果表明，在低雷诺数下鸮翼升阻比较NACA0002和NACA0012等标准翼型均有提高，这说明该截面处的鸮翼有着良好的气动性能。王星等［4］以某长耳鸮翼型为仿生研究原型，通过正交试验研究发现，翼型前缘厚度对仿生翼型升阻比影响最大，随着翼型前缘厚度减少，翼型升阻比增加，翼型下表面中部曲率和翼型尾部厚度均存在使仿生翼型升阻比最大的最优值。李典等［5］通过对于海鸥、秋沙鸭、水鸭以及鸮等鸟类翅膀40%截面处翼型绕流场的数值研究发现，频谱图中鸮翼型声压级明显低于其他三种翼型，这说明鸮翼的特殊结构具有良好的气动声学特性。上述研究表明，长耳鸮翅膀翼型与流动特性有密切联系，然而对于长耳鸮整体翅翼各截面的流动特性及其对噪声的影响尚未见报道，故本文将对此展开较为深入的研究。

本文采用数值方法对长耳鸮翅膀展向20%、40%和60%截面处翼型流场及流动诱导声场进行研究，分析其流动及噪声性能。将三种翼型进行性能对比，利用计算流体力学模拟绕仿生翼型的非稳态流场，分析可能产生扰动的流场结构。

1 长耳鸮翅翼几何参数

由于某长耳鸮翅膀展向20%以下、80%以上截面翼型与展向20%和60%处翼型相似，因而本文对其翅膀展向20%、40%及60%三个典型截面处的翼型性能进行研究，相应的翼型几何参数来源于文献［6］。根据文献［6］，长耳鸮翅膀最大弯度Zc，max和最大厚度Zt，max沿翅膀展向分布有

式中：c为翅翼弦长；ξ为展向相对位置，ξ =y/b，y为展向坐标，b为翅膀展长。

文献［6］同时拟合了各相对展向位置的翅翼的中弧线和厚度分布，得到了光滑的翼型及具体翼型参数。图1为长耳鸮翅膀20%、40%和60%相对展向位置的翼型形状，可以看出：翅根侧20%截面处翼型前缘半径、最大弯度和最大厚度是三者中最大的；而翅尖侧60%截面处翼型前缘半径及弯度均最小，厚度沿弦长的分布也较为平缓；40%截面处翼型形状介于前两者之间。三个截面处翼型均在翅膀飞行做功过程中发挥了作用，因而通过研究可以了解到各个剖面翼型对长耳鸮飞行所作的贡献。

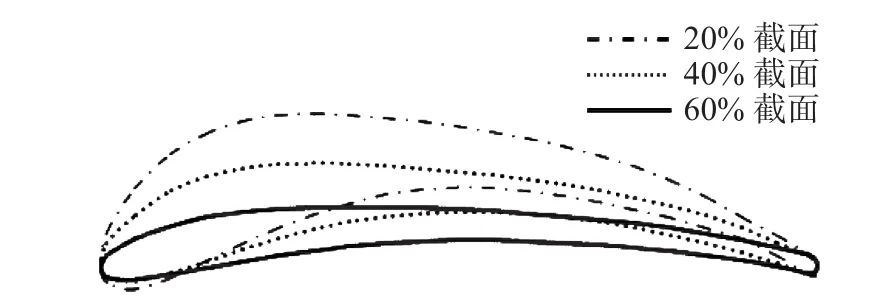
图1 某长耳鸮翅膀展向三个截面处的翼型形状Fig. 1 Airfoil shape of three bionic airfoils based on the long-eared owl wing

2 数值计算方法

2.1 计算网格及边界条件

图2为二维翼型绕流计算域和网格示意图。为了合理地给出边界条件，计算域进口和出口分别位于翼型前缘上游9倍弦长和下游20倍弦长处。为了提高近翼型区域计算网格的正交度，合理布置计算域网格疏密分布，本文采用多区域法进行网格划分，其中近壁区为O型网格，翼型表面法向第一层网格y+＜1，且翼型表面附近的计算域采取加密处理，如图2(b)所示。

图2 二维翼型绕流计算域及网格示意图Fig. 2 Computational region of 2-D airfoil flow and its meshing

本文采用的计算域边界条件有速度进口、自由出流出口边界和无滑移壁面边界条件，其中进口速度均为30 m·s−1，进口雷诺数Re约为4 ×105。为了模拟鸮翼在不同来流攻角（来流方向与翅翼弦长的夹角）下的性能，本文通过改变进口速度方向，在− 5°～20°攻角范围内对翼型非定常湍流场进行计算。

为了验证数值计算结果与网格的无关性，本文首先以40%截面处的翅翼为例进行了网格无关性验证。图3给出了翼型0°攻角下分别取15万、30万、45万、60万和75万网格时的升阻比CL/CD（CL为升力；CD为阻力）曲线，可以看出：网格数从30万增加到75万时升阻比增加量约为网格数从15万增加到30万时增加量的1%，因而认为网格高于30万时，升阻比基本不再随网格数增加而发生改变，表明数值解已不依赖于计算网格。本文综合考虑，将计算网格数保持在30万左右。

2.2 数值方法

鸟类飞行时特征速度一般为20 m·s−1左右，故流体绕流翅膀的流动属于不可压缩流动，因此本文采用不可压缩N−S方程作为流动控制方程，应用Spalart−Allmaras单方程模型进行湍流模拟。控制方程的离散格式为二阶迎风格式，采用SIMPLEC算法求解离散控制方程组。为了捕捉翅翼表面的湍流特征，本文在绕流场定常数值解基础上启动基于大涡模拟技术的非定常流场计算，亚格子尺度模型为Smagorinsky−Lilly模型。在数值计算时，时间步长取为4 × 10−5s。为验证其合理性，首先对20%截面处翼型非定常流场进行了试算，并将监测到的翼型升力和阻力系数经快速傅里叶变换后发现，翼型升阻力脉动主频约为160 Hz左右。该脉动周期约为0.006 25 s，远大于计算所取时间步长，因而判断所取时间步长可以满足模拟计算要求。

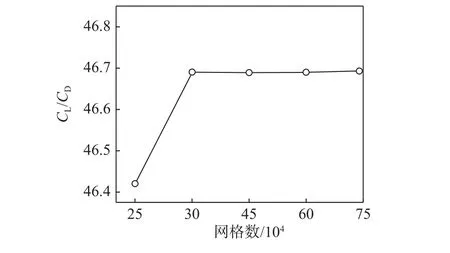
图3 40%截面处翅翼升阻比随计算网格数的变化(α =0°, Re = 4 × 105)Fig. 3 Influence of mesh number on the lift-drag ratio of the airfoil at the cross section of 40% (α = 0°,Re = 4 × 105)

本文采用声学软件Actran计算翼型流场对于远场的声辐射。该软件是基于Lighthill声类比理论［7］的有限元声学软件。对于静止固壁绕流诱导的气动噪声问题，Actran软件通常采用Lighthill体声源方法计算，即将绕翼型的一定区域定义为体声源区，声源区外为声传播区。在声源区，流场速度是Actran计算声源的基础。本文通过非定常流场计算获得一定时间段内声源区所有网格点的速度信息。在声传播区，由于本文研究的翼型绕流马赫数Ma相对较低（Ma ＜0.1），故可忽略声传播区背景流动对声辐射的影响，所求解的声学方程可为

式中：ρ′为流体密度波动量，ρ′ = ρ−ρ′0，ρ、ρ′0分别为扰动、未扰动时的流体密度；t为时间；c0为等熵条件下的声速；为Hamilton算子；i、j为笛卡尔坐标系两个坐标分量；为Lighthill应力张量。

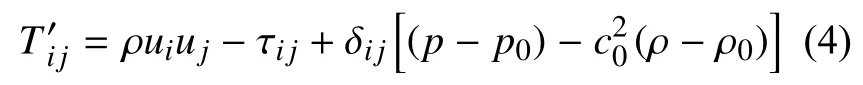
式中：ui、uj分别为液体速度矢量在xi、xj方向上的分量；为黏性应力张量；p、p0分别为扰动、未扰动时流场压力。

为了模拟声在无限区域传播，将最外围边界区域定义为无限元区域，模拟远场辐射，假设声音在此区域内可自由传播，没有反射。

3 计算结果分析

3.1 翼型的气动特性

图4为20%、40%和60%截面处翼型升阻力系数及升阻比。从图中可看出，40%截面处翼型升力系数在大多数攻角下都比其他两种翼型的要高，60%截面处翼型升力系数最小。但是由于20%截面处的翼型厚、弯度大，因而阻力也相对最大，60%截面处的翼型薄且弯度小，其流动阻力相对最小，因此，40%和60%截面处翼型升阻比基本接近，20%截面处翼型升阻比最低。但几种翼型总体上而言都具有良好的流动性能，在5 °攻角下60%截面处翼型升阻比达到了25以上，其余两种翼型均高于45。这也进一步验证了鸟类翅膀具有高升阻比的特性。

图4 20%、40%和60%截面处翼型升阻力系数及升阻比(α = 0° ～ 20°, Re = 4 × 105)Fig. 4 Influence of the attack angle on the lift coefficient, drag coefficient and lift-drag ratio of three bionic airfoils (α =0° ～ 20°, Re = 4 × 105)

图 5（a）、（b）和（c）分别给出了 0°攻角下、进口风速为30 m·s−1时翅翼表面的压力系数分布，图中x为x轴方向坐标。压力系数Cp为

式中：Ps为静压；P∞为无穷远处未受扰动时流体静压；v为来流速度。

由图5中可知，20%和40%截面处翼型的吸力面在0.2倍弦长位置存在局部吸力峰，从翼型前缘到0.4倍弦长范围，吸力面压强变化梯度大。相对来说，60%处翼型表面的压强沿弦长方向分布较为均匀。图5（d）给出了翼型载荷ΔCp沿弦长的分布，ΔCp为压力面与吸力面压力系数之差。可以很清楚地看到，20%、40%和60%截面处翼型的最大载荷均出现在0.2倍弦长位置，值分别为1.94、2.08和1.04，且在较大的弦长范围内，40%截面处翼型具有较大的载荷，这表明该翼型的升力最大。从图5（d）还可看出，20%截面处翼型的载荷沿弦向的总体变化梯度∂p/∂x非常大，而60%截面处翼型的载荷沿弦向变化则较为均匀。20%和60%截面处翼型在最大载荷点前总体变化梯度为16.38和10.97，在最大载荷点后则分别为−85.96和−22.73。显然，压强沿翼型表面的急速变化将改变翼型表面附面层厚度发展规律，从而对翼型的气动特性、附面层内湍流脉动诱导的噪声产生重要影响。

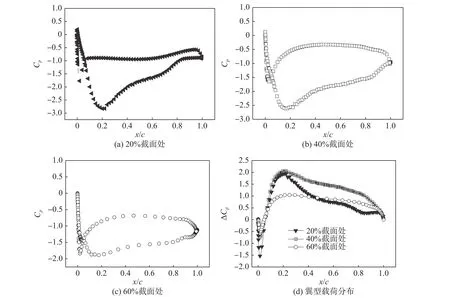
图5 压力系数及压力系数差值分布Fig. 5 Distributions of the pressure coefficient and its difference

图6给出了0°攻角、进口风速为30 m·s−1、时间为0.04 s时速度云图和流线图。由图中可见，20%截面处翼型的压力面存在大范围流动分离，气流在吸力面x/c = 0.35位置也发生了分离，40%截面处翼型压力面的分离范围已明显减小，而吸力面的分离点位置向后移动至0.67倍弦长处。60%截面处翼型的吸力面附面层基本上没有发生分离，压力面在前缘处出现速度分离，但分离范围小，且在0.45倍弦长位置流体再附。翼型表面的速度场分布特征与图5给出的压强及载荷分布特征吻合。

根据涡声理论［8］，气动噪声来源于流场中涡的拉伸和破裂。该理论将气流辐射噪声与涡量场相联系，因此明确流场中涡量的大小、变化和输运情况，对分析流动声源的产生机制有十分重要的参考价值。本文根据对各翼型升力及阻力系数的监测结果，将5 000个时间步长的时域数据通过傅里叶变换为频域信息，得到20%、40%和60%截面处翼型的主频分别为160、407和977 Hz，则各自周期分别约为0.006 25、0.002 46和0.001 02 s。图7给出了三个翼型截面在各自的主脉动周期内的涡量图，间隔为各翼型1/5周期时间。从图7中可看到：20%截面处翼型在翼型前缘有大量的气流分离，随着时间的变化，吸力面上方涡再附后又再次分离，尾缘处也出现稳定的涡脱落，从0.205 40 s至0.206 65 s其压力面近尾缘处出现了很明显的涡发展过程；40%截面处翼型在吸力面上方也产生了气流分离，但其分离点更远离前缘，也可以很明显地发现再附及脱落现象，另外，在尾缘及压力面都有涡产生，尾缘涡脱落现象较为明显，且强度更大；60%截面处翼型在翼型吸力面边界层基本依旧附着，没有很明显的气流分离产生，仅在尾缘及前缘下方处出现明显的涡发展过程。综合而言，20%截面处翼型涡脱落集中度及强度皆大于其他两种翼型，40%截面处翼型次之，60%截面处翼型最小，因而仅就涡流噪声而言，可以预测60%截面处翼型应当为最优，40%截面处翼型次之，20%截面处翼型较差。

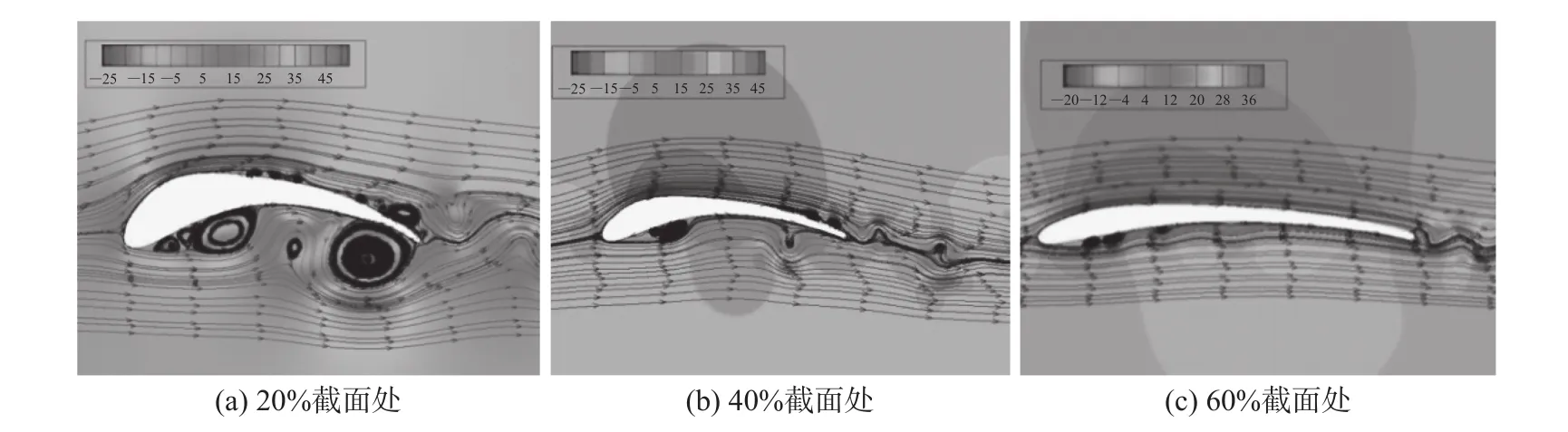
图6 三个截面处瞬态流场翼型速度云图和流线图(t = 0.04 s)Fig. 6 Velocity contours and streamlines of transient flow for three bionic airfoils (t = 0.04 s)

图7 翼型速度涡量图Fig. 7 Vorticity and velocity of three bionic airfoils

3.2 翼型绕流声场分析

为了得到翼型绕流场在各传播方向上辐射噪声的能力，在圆心位于翼型前缘、半径为20倍翼型弦长的圆上布置36个声压接收点，分布情况如图8所示。图9为三种翼型25 Hz下的声压级指向性分布，其中：SPL为声压级，单位为dB。图9表明声压级随辐射方向变化明显，在上下方和左右方均出现明显的高、低峰，说明噪声的主要辐射区在翼型的上下方。可以看出，当进口风速为30 m·s−1、攻角为0°条件下，翼型近壁区涡量最多的20%截面处翼型向周围辐射的噪声最大，40%截面处翼型次之，60%处翼型噪声性能最优。这再次表明涡流噪声是影响翼型噪声的重要因素。

图8 声辐射场点分布情况Fig. 8 Field point distribution of the acoustic radiation

图10给出了长耳鸮翅膀20%、40%和60%截面处翼型的第28个声压接收点的声压级曲线。从图中可知，三种翼型的声压级频谱均呈现出明显的宽频特性，在0～6 000 Hz范围内，三种翼型呈现出随频率较为相似的变化趋势。在此范围内各翼型都有一个声压级低峰值，20%截面处翼型低峰值约出现在3 000 Hz处，40%和60%截面处翼型则出现在约4 500 Hz处。三种翼型最高声压级皆出现在低频处，其大小从20%截面处至60%截面处翼型依次下降，分别为85.8、78.6和74.8 dB，对应频率分别为240、435和 760 Hz。

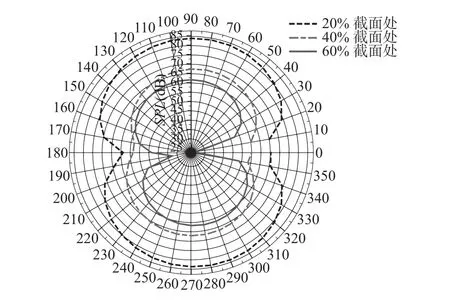
图9 声压级指向性分布Fig. 9 Directional distribution of SPL

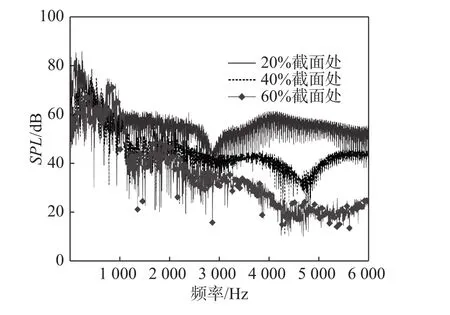
图10 声压级频谱Fig. 10 SPL spectrum

图10表明，在0～6 000 Hz范围内，20%截面处翼型的声压最大，40%截面处次之，60%截面处翼型最小。另外，在低于1 000 Hz频率下各翼型噪声特性皆比较明显，三种翼型差距不大，但高于1 000 Hz之后可以明显地看出，三种翼型噪声特性随频率变化高低有清晰区分。总体而言，20%截面处翼型在各频率下皆产生了最大噪声，60%截面处翼型在高频与低频下的噪音表现基本都较稳定，噪声皆为最低，说明该翼型产生的高频涡流较少，因而此截面拥有最优的噪声性能。

4 结 论

（1）三种翼型均具有高升阻比特性和良好的流动性能。20%和40%截面处翼型具有较高的升力系数。瞬态流场计算结果显示，在强烈的逆压梯度下，这两种翼型气流在吸力面前缘后方产生分离，在下游处产生了明显的不规则涡结构，在脱离尾缘后涡结构发生破碎，并转化成小尺度湍流；60%截面处翼型阻力系数最小，在升力系数并不出众的情况下获得了很高的升阻比。

（2）速度涡量说明三种翼型空气流动时产生的涡大相径庭。20%截面处翼型产生最多的涡流，40%截面处翼型次之，60%截面处翼型则有最少的涡流产生。这直接导致了翼型噪声辐射大小不同，60%截面处翼型噪音最低，20%截面处翼型的则相对最高。

（3）声压级指向性分布说明三种翼型的声源均为偶极子源，并优先向上下方传播，偶极子图案偏向性与翼型弯度有关，频谱图显示声压级会出现先下降后又逐渐上升的趋势。这可能是由于随着流场湍流场的变化，原先产生的频段中的涡结构逐渐消失，之后随频率的增加，高频涡又开始产生引起的。在低频段声压级达到峰值时有明显的噪声特性。三种翼型的噪声特性产生机理及变化趋势基本一致，都有各自的高峰与低峰值。声压级因各自不同的特殊形态结构有高低之分，其中60%截面处翼型低噪特性更优。