牛顿法方程式对渐开线函数的求解及Excel函数实现齿轮参数自动设计

汪奎

（中航工业贵阳万江航空机电有限公司，贵阳 550018）

0 引言

我国齿轮生产已达相当规模，设计与工艺水平不断提高，一些齿轮产品生产已接近或达到国际水平，但总体上还有一定的差距。工程技术人员面对齿轮设计，要面对参数优化、精度等级、毛坯要求、公差与验收，以及大量数据的计算，占用产品设计的大量周期。如何对产品的前期风险进行识别、对齿轮参数进行优化设计和自动计算、减少人工计算量、提高工作质量和实物质量，是本文研究和探索的重点。

1 查表法求取α的弊端

对于不同压力角α的渐开线，可查找专用表格，但查找起来很麻烦、效率低、易出错。例如通过表格查找压力角α=20°15′25″(20.256 944 44°)的渐开线函数。

由渐开线函数表查出α=20°15′=0.0154903和α=20°16′=0.0155299，算出1″为

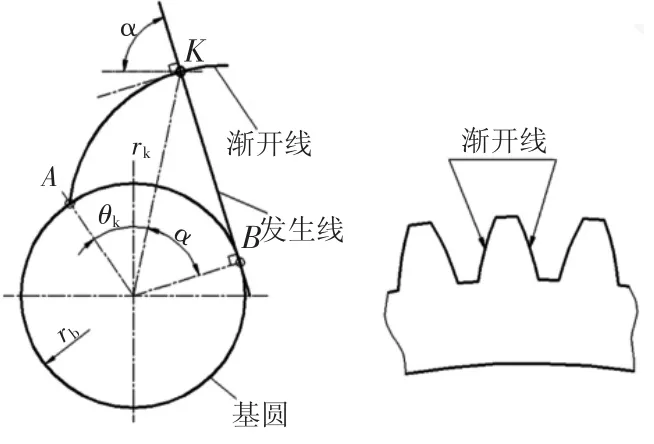
图1 渐开线函数公式推导

所以25″的渐开线函数值用内插法求得为：

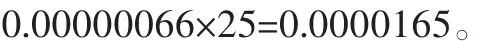
最后计算出:

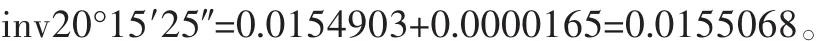
这个过程占用工程技术人员大量时间,而且结果的可靠度低。

2 渐开线函数invα的公式推导

研究渐开线齿轮的啮合原理和计算齿轮厚度等几何尺寸时，常常需要用到渐开线方程式。由于采用极坐标方程式比较方便，所以这里只介绍渐开线的极坐标方程式[1-3]。

如图1，A为渐开线在基圆上的起点，K为渐开线上任意点，其向径为rk，渐开线AK段的展角为θk，在△OBK中，∠KOB=α，

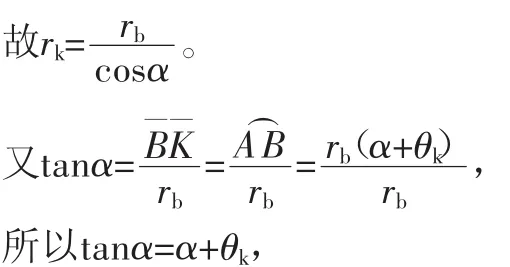
故θk=tanα-α。由此得渐开线极坐标方程：

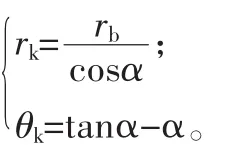
该式表明：θk随α的变化而变化，所以展角θk是压力角α的函数，称为压力角α的渐开线函数。工程上常用invα表示θk，即

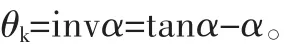
渐开线函数有专门计算好的表格，可以直接查阅标准，对于齿轮参数的设计至关重要。

因此，渐开线的极坐标方程式又可写为：

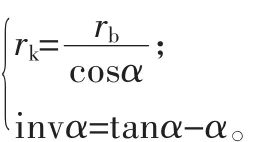
3 正切函数tanα展开成幂级数

3.1 泰勒级数

若函数f（x）在x=x0时连续且有各阶导数，则一般可展开成泰勒级数：

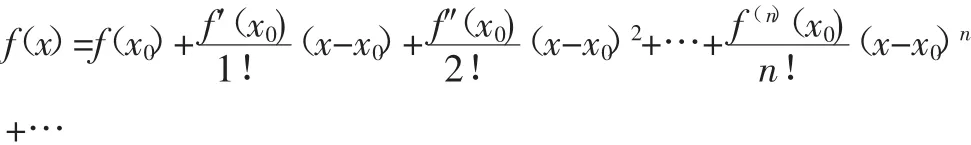
3.2 马克劳林级数

马克劳林级数是泰勒级数在x0=0时的特殊情形：

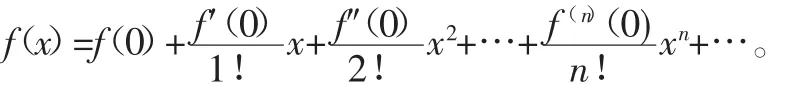
3.3 tan（x）函数展开成级数

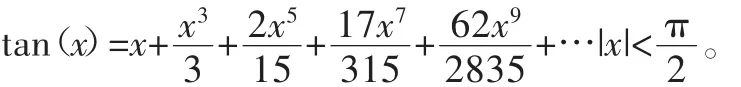
4.1.2 粗略近似值的精确化法。

这里运用牛顿法求解：如果方程f（x）=0有一根c介于［a,b］之间，且f′（x）及f″（x）存在，则可用曲线端点f（b）的切线与x轴的交点x1来逼近曲线与x轴的交点即方程的根c。对于任意第i次近似：

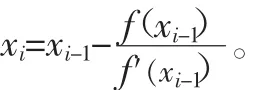
4 牛顿法实现invα=tan（α）-α渐开线方程式的求解

4.1 方程根的求解方法——牛顿法

方程的近似解既可应用于代数方程，也可应用于超越方程。根的计算分为根的粗略计算和将根的粗略近似值精确化两步。根的粗略估算法有试验法、图解法、拉格朗日法等；根的粗略近似值精确化方法有弦线法、牛顿法、迭代法等。由于牛顿法收敛速度较快，这里我们采用牛顿法求解。

4.1.1 根的粗略估计法

主要根据应用实践进行选取。根据invα=tan(α)-α的特殊情况，初步估计根的区间为

可以连续求下去，直到所需的精度为止。

4.2 invα=tan（α）-α的求解

以invα=0.0155068为例，求取α值。首先需要将tan(α)展开成α的函数关系式，这里，我们运用函数展开成幂级数的形式:

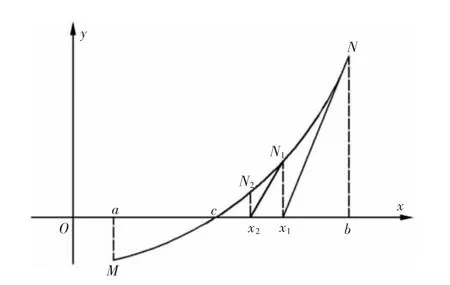
图2 方程根近似值的精确化法（牛顿法）

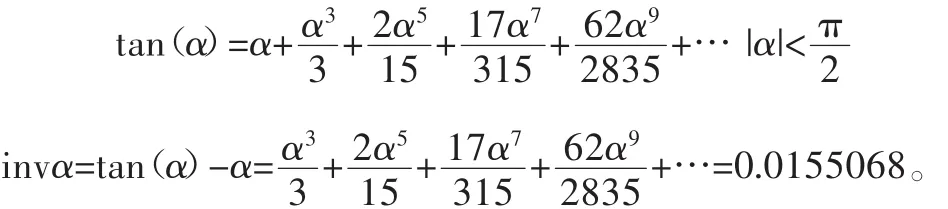
取级数中最前面5步进行计算和迭代：

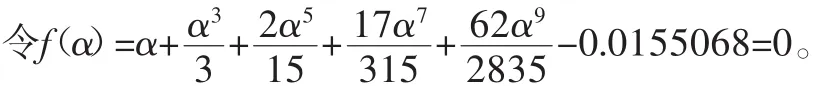
则

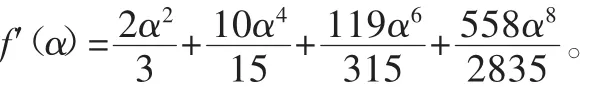
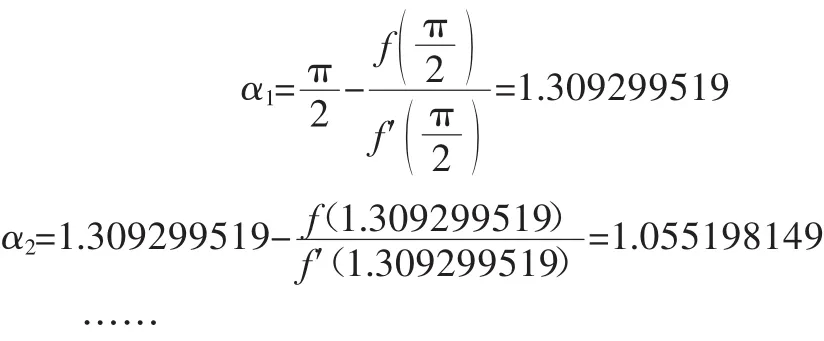
当迭代到第9次时，

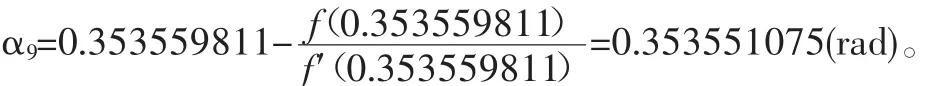
换算为角度值为20.25698443°，离目标值20.256844 44°已经非常接近，两者相差：20.25698443-20.25684444=0.00013999，误差不到0.14‰，已相当精确。迭代次数越多，越接近目标值。

5 齿轮参数自动设计

涉及到齿轮参数的计算很多，如圆柱测量距、公法线长度及跨齿数、任意半径齿槽宽、公差组参数值等等，由于涉及到的面比较广，我们仅举一个例子，如何运用常用软件Excel的强大函数功能，实现斜齿轮（外齿、双数齿）圆柱测量距M的自动设计。

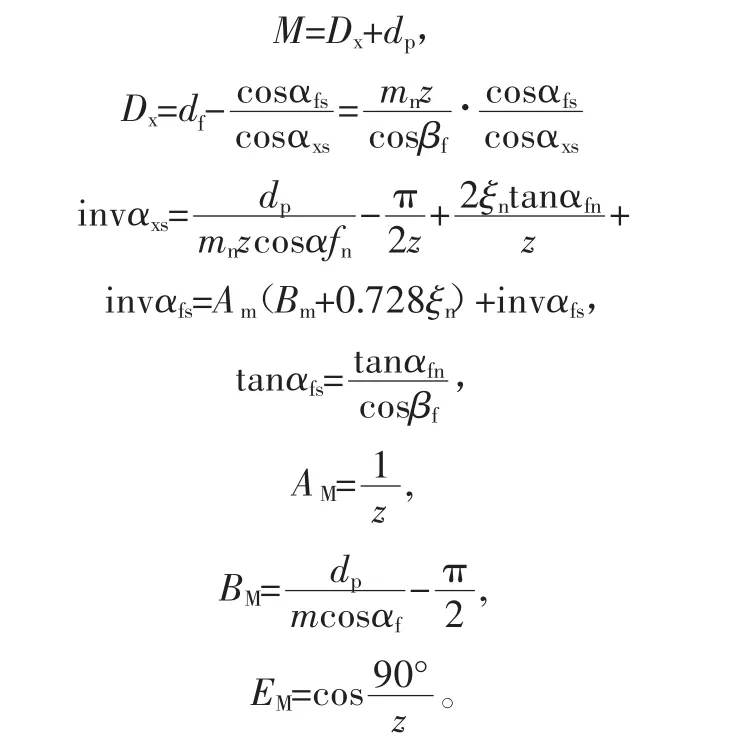
式中：df为分度圆直径；dp为圆棒直径；mn为法向模数；αfn为法向分度圆压力角；αfs为端面分度圆压力角；ξn为法向变位系数；βf为分度圆螺旋角。

假设：mn=0.6 mm，Z=42，α=20°，βf=4°53′57″，ha*=1，C*=0.35；dp=1.008。Excel单元格设置：mn=B2、Z=B3、α=B4、βf=B5、ha*=B6、C*=B7，ξn=B8、dp=B9。

运用牛顿法方程式自动求解出invαfs(单元格D13)，进而计算出：

invαxs==B9/(B2*B3*COS(B4*PI()/180))-0.5*PI()/B3+(2*B8*TAN(B4*PI()/180)/B3)+D13=0.02022820

Am=1/B3=0.02380952

Bm=B9/(B2*COS(B4*PI()/180))-PI()/2=0.21702233 Em=COS((90/B3)*PI()/180)=0.99930071(D20)

Dx=B17*COS(D14*PI()/180)/COS(D16*PI()/180)=25.63368296(D17)

M=D17+B9=26.64168296。

一般四舍五入到小数点后3位精度足够，即M=26.642。

6 结语

齿轮参数的设计比较复杂，特别是大量繁杂的公式计算是工程技术人员不得不面临的课题。本文结合工作实际，利用牛顿法对方程的求根方式，并用生活中最常用的Excel软件的函数功能，成功地解决了这个问题。经过10多年在公司的成功运用，特别是军工产品机械加工领域，取得了很好的效益。创新的思维可以解决复杂问题，小创新带来大进步，这是每个工程技术人员的义务。