基于MATLAB语言的凸轮轮廓曲线的解析法设计

杜韧， 冯伟娜， 刘昭， 刘宏伟， 毕珊珊

（北华航天工业学院机电工程学院，河北廊坊065000）

0 引言

凸轮机构结构简单而且紧凑，能传递较大功率以及任意传动比的传动，同时它还具备了控制、传动、引导等各项功能，可以实现各种各样期望的议案，已广泛在各种机械自动控制的广泛应用中使用[1]。所以，对于凸轮机构的深入研究，特别是对高速高精度凸轮机构的设计、制造等各个方面的进一步研究是一项十分重要的工作。

凸轮机构是一个具有曲线轮廓或向内凹的曲线槽的常用的构件，大多数情况下作为主动件，按外形可分为盘形凸轮、圆柱形凸轮和移动凸轮等。通常情况下从动件与凸轮作点或线接触，其中滚子推杆与凸轮做滚动摩擦，使得两者之间因为摩擦而受到的损失都非常小，且工作时产生的噪声也很小，因此可用于动力传递较大的结构，有其他形式从动件所没有的特点，应用十分广泛[2]。凸轮一般情况下作等速的回转运动或者是简单的往复直线运动。由于凸轮的轮廓曲线可以决定从动件的运动规律，故绘制凸轮轮廓曲线具有一定的现实意义。

现在关于凸轮轮廓曲线设计一般分为两种：一种是传统的图解法，一种是解析法。其中传统的用作图方法来绘制凸轮轮廓曲线有很大的弊端，不仅工作量很大，而且精确度不高。通过人工处理，把这些通过试验测得数据描绘成曲线，往往会出现很大的差错，并且不同的人产生的误差也有所不同，特别是对于一些精确度高的试验，更不

基金项目：河北省研究生创新资助项目（CXZZSS2017173）;北华航天工业学院科研创新项目（YKY201502，YKY201616）能采用传统的人工处理方法，否则就会严重影响数据的准确度以及图形的精度。解析法可以精确计算轮廓线上各点的坐标，误差比较小。当从动件运动比较复杂，工作量大时，用MATLAB软件可以很容易进行凸轮轮廓曲线的解析法设计[3-15]。

本次设计选择的是摆动从动盘形凸轮机构，利用MATLAB强大的数据处理、绘图功能对凸轮的运动规律进行运动学仿真，首先运用公式计算出凸轮理论轮廓线上和实际轮廓线各点的坐标[16-17]，然后在MATLAB中通过绘图指令plot可以完成直角坐标系下凸轮轮廓曲线以及对推杆的位移s、速度v及加速度a曲线的绘制，且相比传统的图解法，精确度更高，拟合更好。

1 总体设计方案

1.1 推杆的运动规律

通常情况下，要完成凸轮机构的设计任务，推杆的运动规律和凸轮的相关尺寸是根据所给定的条件以及凸轮机构的类型来决定的，然后根据所决定的推杆的运动规律通过一系列的计算，设计出凸轮应有的理论轮廓曲线以及实际轮廓曲线。所以说选择合适的推杆的运动规律至关重要，这不仅关系到接下来研究的难易，还关系到凸轮机构的工作质量。

通常来说，推杆的运动规律，就是推杆的位移s与时间t，速度v与时间t和加速度a与时间t之间的变化规律。摆动从动件盘形凸轮经常情况下为等速运动，推杆的运动规律可以用推杆的运动随凸轮转角δ变化而变化来表示。其中余弦加速度运动规律的加速度曲线在开始的时候运动有急剧的增加或者急剧的减小，在结束时也会发生这样的状况，所以也会有柔性的冲击，这种运动规律的凸轮结构只适用于中速凸轮机构。如果从动件在整个运动过程中不会停止时，加速度的曲线是连续不断的，因而就不会发生冲击现象，这种情况下就适用于高速凸轮机构中，具体公式如下。

推程时从动件的运动方程为:

1.2 凸轮轮廓曲线的设计

根据设计要求选定了凸轮结构的型式，以及设计要求中的基本尺寸，计算所得的推杆的运动规律及计算出的凸轮的转向后，接下来就该进行凸轮轮廓曲线的设计了。

凸轮轮廓曲线设计所依据的基本原理是反转法原理（图1）。反转法原理：根据相对运动原理，假设整个凸轮机构绕凸轮轴心施以角速度－ω时，这种情况下各个部件的相对位置发生改变，但是相对运动不变，这样一来，凸轮可以看作静止的，而从动件接触点复合运动的轨迹就是凸轮的理论轮廓曲线。

具体轮廓曲线的方程会在下面数学模型中列出。

图1 凸轮反转法示意图

2 凸轮机构的设计流程和数学模型

2.1 凸轮机构的设计流程

1）输入凸轮结构的参数，如从动件滚子半径、盘形凸轮的基圆半径、摆动从动件的长度、凸轮推程运动角、从动件最大位移、远休止角和回程运动角等；2）计算摆动从动件凸轮机构的最大压力角和在理论轮廓上最小曲率半径使其不超过规定的许用值（否则会发生失真现象）；3）计算凸轮的理论轮廓的坐标；4）计算凸轮的实际轮廓坐标值；5）绘制凸轮轮廓图形。

图2 摆动从动件盘形凸轮机构

2.2 建立数学模型

建立关于摆动从动件盘形凸轮机构的数学模型，如图2所示。

理论廓线方程为：

式中：a为中心距；l为长度；δ为凸轮的转角；φ为盘形凸轮的角位移；φ0为推杆的初始位置角，其值为

盘形凸轮实际轮廓的对应点（x′,y′）的方程为：

其中，rr为滚子半径。

凸轮理论轮廓上的机构压力角

式中：e是盘形凸轮的偏距；s是推杆产生相对的位移。

凸轮理论轮廓曲线上的曲率半径为

凸轮轮廓直角坐标的一阶导函数:

二阶导函数：

因此，利用解析法来求出凸轮轮廓,需要从动件运动规律相对应的函数关系，对应地求导其一阶导函数ds/dδ和二阶导函数d2s/dδ2,然后将这些导函数代入到式（1）~式（7）中进行计算。从余弦加速度运动规律上可以看出，回程位移与推程位移之间有一定关系，计算回程时的从动件运动规律中凸轮转角取值范围为δ=0~δo′;计算凸轮的理论轮廓直角坐标及其导函数公式中的sinδ、cosδ的凸轮角取值范围是：

3 用MATLAB软件进行仿真

3.1 主要使用的功能函数和命令

在MATLAB软件平台进行凸轮轮廓设计,主要使用的功能函数和命令是:1）for-end循环。以凸轮转角δ作为循环控制变量，实现对凸轮某个运动角或整周区域的轮廓计算。为加快运行速度，可在循环结构执行之前建立全零数组命令zeros(n)预先定义数组的大小。2）if-else-if条件语句。检查凸轮转角δ满足的区域（推程运动角，回程运动角或休止角范围）条件；或在凸轮某个运动角区域的传力性能参数（如压力角）或结构参数（如轮廓曲率半径）数组中满足极值的条件，然后执行相应的运算。若需要在满足一定条件时打破循环时，可使用break命令。

关于凸轮轮廓图形处理程序编制是有以下几点需要注意:1）为了将理论轮廓、实际轮廓、基圆等多种线图在同一个图上显示出来，应该采用了hold on命令；2）使用了axis equal命令，这样就不会再发生让图形窗口中因为（x，y）坐标轴的不同的比例而造成图形失真这一现象；3）使用text和 title标注图形和图题;利用plot命令中，用不同的颜色，不同线型参数来描绘同一个坐标轴上不同的线图，使图形表示更加详细，更容易让人看懂，不会造成混淆；4）使用legend根据曲线属性添加图例说明，便于区分各个曲线的具体含义和内容。

3.2 滚子从动件各阶段MATLAB程序编制

根据建立的数学模型，利用MATLAB中函数编辑后计算出来，求出所需设计的凸轮的理论，实际轮廓曲线，并且利用plot函数进行制图，把从动件运动时的加速度a、速度v、位移s利用己有函数画出来，并进行盘型凸轮与滚子从动件之间运动学仿真。

4 M文件以及运行结果

4.1 M文件

编写M文件来求出凸轮的轮廓曲线，基圆半径，推杆的运动规律。其中所需要的数据有：摆杆转轴到凸轮轴心的距离a=160 mm；摆杆长度l=100 mm；滚子半径rT=10 mm；推程运动角φ=120°；回程运动角φ′=150°；远停程角φs=30°；摆杆最大角位移30°；初始位置角φ0=15°。等角速度ω逆时针方向转动，余弦加速度运动规律。M文件具体如下：

4.2 MATLAB仿真运行结果

由MATLAB编辑的M文件可以得到摆动从动件盘形凸轮机构的基圆、理论轮廓曲线和实际轮廓曲线，以及推杆的位移曲线、速度曲线和加速度曲线，具体如图3~图6所示。由图3可以清楚地看出凸轮机构的理论轮廓线、工作轮廓线、基圆半径，由图4~图6，我们能直观地看出凸轮从动件的运动规律。

图3 摆动从动件盘形凸轮的理论轮廓曲线和实际轮廓曲线

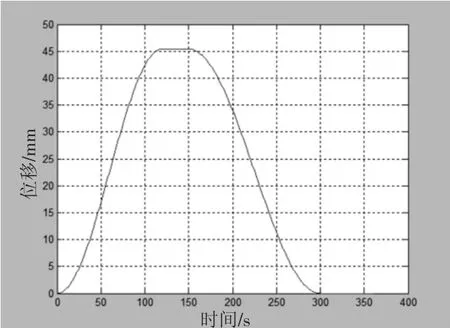
图4 从动件位移曲线

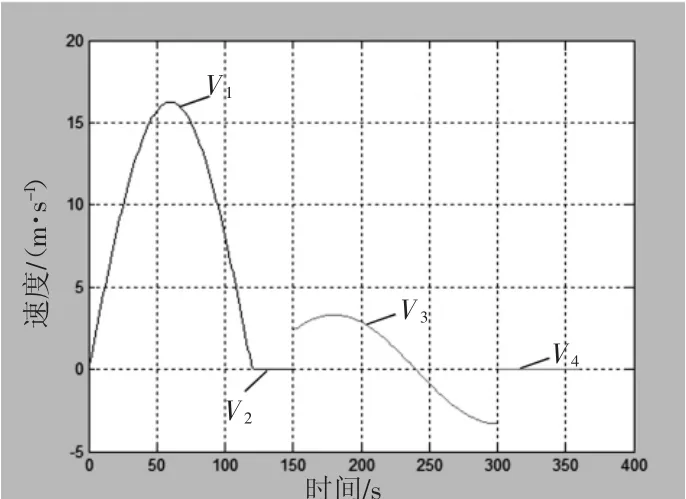
图5 从动件的速度曲线

图6 从动件的加速度曲线

5 结语

本文利 用MATLAB软件对摆动从动件盘形凸轮机构的运动进行了分析，此软件可简捷、方便、直观地反映出从动件的速度与时间的关系、位移与时间的关系以及加速度与时间的关系，应用MATLAB软件可以很直观看出凸轮机构的轮廓曲线，对研究凸轮机构的运动具有很大的现实意义。