浅谈小学几何直观的阶段性呈现
江苏东台市三仓镇小学(224231) 崔卫红
几何直观研究的对象涉及数学的方方面面。“几何”是媒介,“直观”是方式,是指对学习材料的直觉感知。空间变换思维能力是“几何直观”成立的基础。几何直观以几何体为信息传输的载体,要求学生不仅要熟练掌握几何图形的性质和特征,还要具备一定的图文转换能力。培养学生几何直观能力可分为三个阶段:孵化阶段→过渡阶段→强化阶段,每个阶段都有自己的特色。
一、孵化阶段,材料抽象要逐步递进
几何直观的孵化阶段主要集中在一、二年级,但此时的直观教学往往采用道具、图片、视频等载体,严格说,算不上几何直观。而且这两个年级段的学生依赖动作思维开展学习活动,为迎合学生的口味,教学要采用直观教学法。如果适当抽象,则能进一步孕育出几何直观的雏形。如对于“100以内数的认识”这个知识点,人教版教材是利用小棒来推演数的递增。这是用客观实物来演绎数学知识,称为实物直观。如何将其逐步升级为几何直观呢?教师要精心挑选教具。首先考虑回形针或木棒,将它们按“10个为一小堆”“100个为一大堆”摆放,分别对应计数单位“十”和“百”;接着换成木块,1块代表“一”,10块排成一列代表“十”,10列连成片代表“百”。仔细比照甄别,就会发现,木块虽是实物,但它的外形具备“点—线—面”的几何特性,能为计数单位“千”(立体)的推出奠定基础,如图1所示。这样的实物模型和演示结构有利于学生搭建起数学模型和计数单位之间的桥梁,为发展学生的几何直观能力夯实基础。
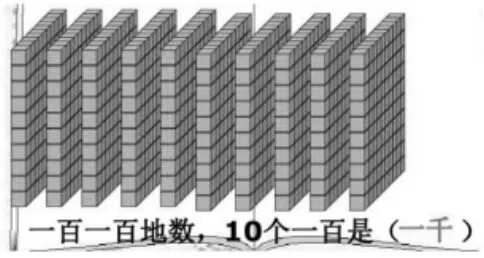
图1
二、过渡阶段——积累经验,培养意识
“几何直观”的准确性建立在长期的经验积累和直觉判断上,而数学活动经验的积累必须建立在对数学知识的建构上。简易平面图形的认识集中出现在三、四年级,如线段、角、各种多边形,因此这一阶段为发展几何直观的过渡期。这一阶段的教学既要重视实践活动的开展,又要注重反思总结,帮助学生将过程记忆升级为思维记忆。
例如“三角形的内角和”的教学,我让学生通过三个实验去验证:1.测量三角形的所有内角,求和;2.裁剪三角形的三个角,组装成一个平角(如图2);3.通过折叠,将三角形的三个内角凑成平角(如图3)。

图2

图3
实验虽然存在一定的误差,但还是很有必要的,其价值在于给学生提供实验的经历,使之从中获得直观体验。综合上述三个实验的精华,学生就有可能提炼出一种平面图形的几何直观(如图 4)。
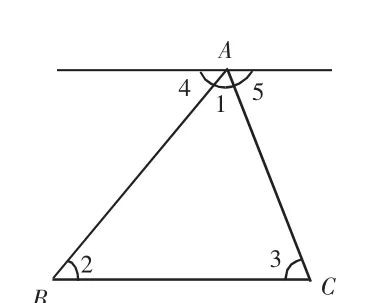
图4
四年级的时候,学生的几何直观能力发展迅速。一方面,这时候的学生掌握了一定的几何基础知识,另一方面,数学知识越来越抽象,必须借助大量的直观材料来支撑思维过程,实物载体慢慢演变为图形字符载体,几何直观开始显现。此时,教师要注重培养学生的几何直观意识,促使学生在分析解决问题时主动利用几何直观来辅助推理。学生几何直观意识的提高依赖于对几何直观价值的认可。因此,教师在教学中要突出几何直观的优越性和先进性。例如“异分母分数加、减法”的教学中,学生计算“”时一般会出现三种情况:(1)
对此,教师要设法让学生理解通分的道理和缘由,指明分数加减也是相同数位上的数字进行相加减,或者相同计数单位的加减。教师可以利用“分数墙”(如图5)来解释。

图5
观察“分数墙”可知,相邻两行之间的单元块代表不同的分数单位,因此不能直接相加,于是我引导学生寻找能代表的单元块。从“分数墙”可知,等同于等同于,经过转化,计数单位相同,可以直接进行加减,得出,即
三、强化阶段,深层推进数形结合
五、六年级时,学生的几何直观能力已经较强,几何直观能力的进一步发展必须建立在数形转化的基础上。数形转换,就是要随时将数码字符和几何图形进行互通互联,让学生的思维在图形和数字之间自由切换。教学中,教师可以结合具体教程制作图形,强化读图训练,也可通过趣味游戏活动,训练学生的数形转化能力。
例如,教学“正方形数的认识”时,出示图6,先要求学生观察并思考“每个点阵共有多少个点?排阵有什么规则?”,从而提出“正方形数”的定义。接下来,通过勾画图形建立算式模型,如点数为n2时,为面积求法的模型;也可表示为等差数列求和:1+3+5+…+n;也可以表示螺旋式求和:4+3+3+2+2+1+1;还可以划分为三角形:1+2+3+…+n+…+3+2+1,如图 7。

图6

图7
像“三角形数”“正方形数”这样的点阵计数法,将点数用几何图形的方式表现出来,数与形高度统一,既可以体现数字的几何特性,又可以将几何图形的周长、面积等用数字解析出来,十分有助于学生几何直观能力的发展。
纵观小学数学教学,学生的几何直观能力培养是一个波浪式前进的过程,需要长期跟踪辅导和磨炼。本文划分的三个阶段也是笼统模糊的,各阶段之间并非泾渭分明,而是渐变过渡的。但是这三个阶段已能指明几何直观能力发展的大方向,为教师在教学中渗透几何直观提供重要参考。

