例谈如何在教学设计中有效渗透数形结合思想

福建厦门市海沧区东孚中心小学（361000） 杜 娟

“数与形”是人教版教材六年级上册作为新增内容编入的，旨在让学生通过自主探究发现图形中蕴含的代数关系，尝试运用代数关系解决几何问题，体验数字与几何图形的微妙关系，同时领悟数形结合的思想。然而，要想在教学中有效渗透数学思想，就必须开展科学的学习活动。那么，怎样的活动才有利于数学思想的渗透？活动中如何体现数学知识和教育理念？这些都是值得深究的问题。

一、在深度思考中领悟数形结合的思想

数学思想如果没有思考的基础，就是空中楼阁，只有对数学知识进行深度思考，才能对知识表象背后的深层思想心领神会。因此，在教学中，教师应引导学生在数形结合的关节点进行深挖，并巧妙地诱导学生比较，让学生在连续的思考中自发领悟。

【教学片段1】

1.观察数字：观察数字25的特征

师：认真观察并揣摩数字25，分析它具有哪些特征？

生1：除了1和本身，25只有因数5。

生2：25可以分解成5的平方，是一个平方数。

生3：25的前一个数是24，后一个数是26，这三个数都是合数。

……

2.化数为形：用图形表示数字25

师：用25枚围棋子摆图形，猜测一下这个图形可能是什么呢？

生：正方形。（让学生用磁扣摆出正方形）

3.以形解数：借用图形探究25的特征

让学生依据课堂提供的正方形点阵（如图1）探寻数字25的特征。

生1：25=1+2+3+4+5+4+3+2+1。（以对角线为视点叠加）

生2：25=（1+2+3+4）×2+5。

生3：25=1+3+5+7+9。

4.在比较中体会

师：摆出方阵，数字25的特点就一目了然了。回顾以上过程，大家有什么感想？

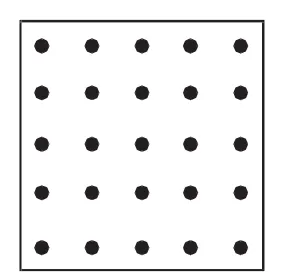
图1

生1：图形的作用真大。

生2：图形可以展现数字背后的奥秘。

生3：有了图形，便可以更直观地列出算式。

以上步骤是教学本课的重点和主轴。教学时摒弃教材提供的正方形素材，改用点阵图，这样改动，一方面考虑到点阵可以呈现出不同的视角，而正方形图无法斜着分；另一方面，点阵图返璞归真的研究方法，实际上完整再现了数学知识发生、发现的过程，使整个学习过程变得连贯。如此设计教学有利于加强数形结合意义与作用的渗透。学生比较后认识到数形结合的优越性和重要意义，切实感受到数形结合的巧妙之处。

二、在发现中感知数形结合的作用

【教学片段2】介绍“神奇的图形数”（三角形数、四面体数、金字塔数等）

多媒体演示：1，4，9，16。

师：现在我们穿越到古石器时代，用石头摆出这些数字，它们可以摆成什么形状呢？

生1：正方形。

师：这样的数字叫什么？（课件出示图2）

生2：正方形数。（平方数）

多媒体演示：1，3，6，10，15。

师：继续用石子摆数字。

生3：这些数字可以摆成三角形石阵。

师：这次又该如何命名？（课件出示图3）

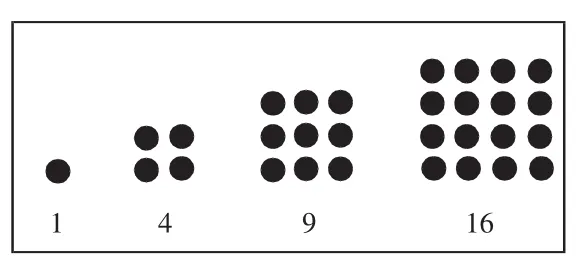
图2

图3

生4：三角形数。

师：观察相邻数之和，你有什么发现？

生5：1+3=4，3+6=9，6+10=16，10+15=25。

生6：相邻两数之和都是平方数，可以用正方形石阵表示。

师：为什么会这样？这其中究竟有什么奥秘？

生7：道理很简单，从点阵图（如图4）可以看出，两个三角形数对拼，刚好凑成正方形数。

接着，用同样的方法研究金字塔数与四面体数。（如图5，过程同上，略）

图4

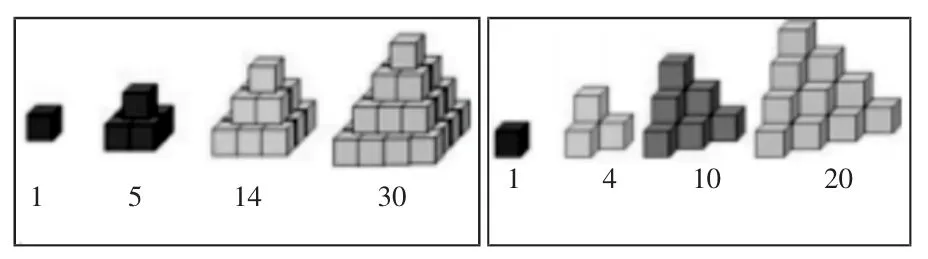
图5

如果不借助点阵图，光凭数字学生很难发现数列“1，4，9，16”具有什么规律，而利用点阵图将这些点数排布成正方形，其特征就显而易见了：这些点数刚好可以排列成行数和列数相等的平面图。几何图形可直观地将数字内部规律展现得淋漓尽致。同样地，对于三角形数列“1，3，6，10，15”，学生很难理解相邻两个数字之和为什么等于平方数，但是，将数字转换成点数并将其排列成三角形后，通过对拼，就可以直观地发现相邻的两个三角形点阵拼成了正方形点阵。

三、在应用中感悟数形结合的价值

任何原理和思想的价值只有在应用中才能得以体现。

【教学片段3】应用数形结合思想解题

师：你能仿照“25=1+3+5+7+9”模式列出其他算式吗？

生1：36=1+3+5+7+9+11。

生2：49=1+3+5+7+9+11+13。

……

师：这就是触类旁通。你能根据自己发现的规律解决下列问题吗？

多媒体演示：1+3+5+7+…+（100个连续的奇数）=。

生3：100×100=10000。

生4：分析原有算式我们发现，5个连续奇数相加，和为 25，25=52；6 个连续奇数相加，和为 36，36=62。以此类推，100个连续奇数的和应为1002。

要发掘出隐藏在算式内部的规律，必须以上文提到的点阵法为基础，将其转化为点阵图来理解，再利用割补法，将倒数第一行右下角多余的4个点剪切到第一行的空缺处，将倒数第二行的2个点剪切到第二行的空缺处（如图6），刚好形成5行5列的正方形点阵。学数学不能没有想象，想象催生发现，在理解了数形结合的思想后，只要大胆想象，就可以创造出更多结合的方法。

图6

对数学思想的领悟和吸收，势必要经历从抽象到具体，从朦胧到清晰的转化过程。本课“数与形”的教学，以“数形结合”思想贯穿始终，精选教学素材，巧设活动，让学生经历思索、联想、探究、运用等有序活动，在活动中让学生不断提炼结晶，反复琢磨沉淀。显然，学生只有经历这样的探究过程，才能深刻理解学习内容中富含的数学思想。