例谈如何发展学生的空间几何观念
江苏如皋市白蒲小学(226500) 张 兵
【题目】如图1,在正方形点阵图上,确定点D的位置,使四边形ABCD构成一个梯形,D点的位置可能有( )。
A.2 B.3 C.4 D.5
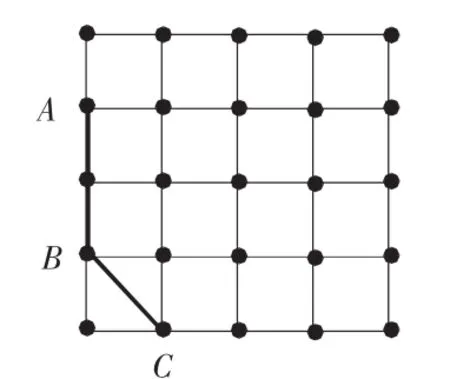
图1
图2为答案解析图,其中图形①至⑤为5种梯形所对应的顶点
位置,图形⑥是构成平行四边形所对应的顶点位置。

图2
此题的答对率只有20%,学生出错原因主要有:(1)无法读懂题意;(2)只考虑将AB作为上底,没有考虑到将其作为下底的情况;(3)加入图形⑥,误将平行四边形算在其中。
一、现象级错误的背后原因
这道题属于“几何图形”的知识范畴,重在考查学生的空间读图能力。课程标准指出:在几何图形教学中要丰富认识,建立立体观念,发展形象思维。那么,如何培养学生的空间观念,是一个值得深究的问题。
1.教师层面
对于该课,一些教师仍然认为“掌握梯形的特征”是教学目标,片面强调“只有一组对边平行”,而忽视了深层原因,忽略了发展学生空间观念的重要性。造成这种不当认识的原因是:图3中的图形③④⑤只是方位发生旋转,但形状一样,只有图形⑥的摆放方式符合学生观察梯形的视觉习惯。
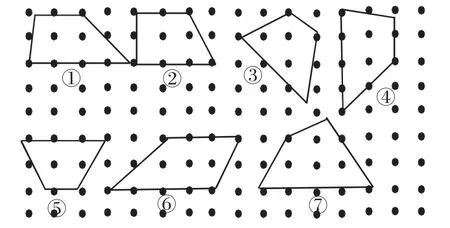
图3
2.学生层面
在学习梯形前,笔者以上图为研究材料进行测试,统计数据如下:

图形① 图形② 图形③ 图形④ 图形⑤ 图形⑥ 图形⑦认为该图形是梯形的学生所占的百分比100% 100% 15.4% 27% 87% 18% 59.6%
通过交流,学生认为:图形⑥与现实生活中的模型出入较大,而图形⑦相似度最高。由此可见,学生只能从生活经验中认识梯形,而没有抽象出几何意义上的梯形。
由于以上各种原因,再加上题目的灵活变换,学生的错误率较高也情有可原。
二、起步和承接
基于以上原因,教师应对“梯形的认识”的教学思路进行调整,不妨以“起→承→引→合”的教学模式,由浅入深,紧紧抓住“只有一组对边平行”这一根本属性,使学生从不同角度认识各种梯形。
“起”则为开端,要结合旧知和经验,导入新课。
由于学生已经熟悉“平行四边形的两组对边分别平行”,因此,课始以平行四边形的这一特征导入,用三角形和平行四边形重叠的公共区域引入梯形概念(如图4),整合两种图形的特征,构建梯形的概念。

图4
在重叠图中引出梯形后,学生会发现新图形挪用了平行四边形的一组对边,同时借用了三角形的两条非平行边,这四条边组合到一起,形成梯形的特征——一组对边平行,另一组对边不平行。这样就把梯形的特征刻画得更细致全面。
“承”则为顺承。顺承导入环节,制造变式,解决相似的问题。
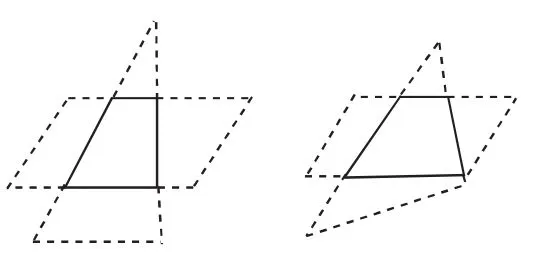
图5
教师出示两种叠放方式(如图5),然后提问:“变换叠放方式后,重合部分都是梯形吗?”教师引导学生观察,发现重合部分虽然形状发生变化,但本质特征仍是“一组对边平行,另一组对边不平行”,这样也就抓住了梯形的本质属性。
在学生理解梯形的本质特征后,教师要联系生活实际,引导学生从“几何图形”视点审视周围的物体,以加深学生对梯形特征的理解。
三、引学结合,活用练习
“引”则为引导,让学生主动参与,运用梯形特征解决问题。
例如,“根据梯形的特征,一刀将一个长方形剪成梯形,观察这个梯形有什么特征”是一道开放性较强的综合实践题,因为剪裁时必须满足构成梯形的条件,也就是打破一组边的平行性。若要剪出一般等腰梯形,需将长方形对折。学生只有对“梯形只有一组对边平行”这个知识点熟练掌握并灵活运用,才能在推理想象中完成对长方形的剪裁,将其转变成梯形。

图6
“合”则为结合。联系前后知识,内化本质特征,发展空间几何观念。空间几何观念的培养需要一个长期过程,教师只有持续培养学生的思维,才能完成这一过程。
学生所形成的空间几何观念应该是“整体的,深刻的,概括的”。学完所有四边形后,教师可让学生把图7中的四边形分类。在分类过程中,学生自然就理解了不同四边形的性质和特征,在与其他四边形的对比中进一步巩固了梯形的特征,并以此辐射到整个四边形体系。

图7
总之,学生空间几何观念的培养是一个漫长的过程,需要教师耐心培养。教师在教学中要抓住几何图形的本质,引导学生在实践操作中学习几何图形的知识,进而强化学生的空间几何观念。

