培养学生几何直观能力初探
江苏苏州高新区实验小学校(215011) 马邹英
皮亚杰指出,儿童的思维水平处于“具体运算思维”阶段,也就是说,儿童对事物的认知离不开直观材料的支撑。因此,教师在教学中要借助直观表象让学生形成“运用直观表象解决问题”的意识,在加深对数学概念的理解的同时,发展几何直观能力。
一、用图,为几何直观筑基
用图就是根据教材提供的插图揣摩题意、捋清数量关系、分析解题方法,从而解决问题。
1.根据几何图掌握数学概念
几何直观是学生的形象思维过渡到抽象思维的阶梯,它可以刻画数学概念的性质,帮助学生更好地理解数学概念。
例如,苏教版教材五年级下册的“真分数和假分数”中,认识假分数是教学难点,因为都是真分数,可以在一个单位“1”内讨论完成,但是假分数超出一个单位“1”的范畴。课堂上,笔者让学生小组合作探究的意义,并让学生上台展示不同的表示方法。
第一种方法:用两个圆表示两个整体,每个圆都分成4等份,第一个圆全部涂色,第二个圆选1份涂色。
第二种方法:用两个圆表示两个整体,每个圆都分成4等份,第一个圆选取3份涂色,第二个圆选取2份涂色。
第三种方法:用三个圆表示三个整体,每个圆都分成4等份,前两个圆都选取2份涂色,第三圆个选取1份涂色。

图1
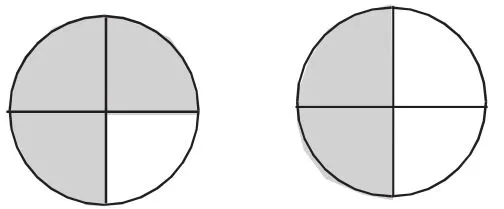
图2

图3
2.重视表象和语言的转换
几何直观可以用直观图形将抽象的数学语言表示出来,实现表象与语言的统一。
例如,苏教版教材六年级上册的“百分数”,教学例10(某粮仓要往省外调拨一批大米,已调走60%,剩下的大米为48吨。这批大米一共多少吨?)时,教师可以指导学生根据题意填充线段图(如图4),然后根据线段图复述题意,分析条件,寻找等量关系式(调走的重量+余下的重量=总重量)。

图4
先审题绘图,再观图出题,最后在图中找到等量关系的学习过程可以提高学生的几何直观能力。
在多元化教育形式下,几何直观不能停留在用直观图形分析、解释题意和运算过程的层面上,还要对学生提出更高的要求——从看图、读图转变为“用图”,在使用图形的过程中表达思维,用图形工具代替文字语言,从被动接受知识转变为主动运用知识,变参照图形解题为使用图形解题。
二、造图,形成创造性思维
几何直观能够让抽象的问题变得具体,让复杂的问题变得简单,从而让学生能快速看透问题。因此,根据题型“造出”合适的“图”对解题很有帮助。
例如,在苏教版教材五年级下册“3的倍数的特征”中,教材让学生将百数表中所有3的倍数找出来。在找的过程中,学生发现按以往的经验无法从“个位”发现解题规律,于是便转换思路——通过拨动算珠来探究问题。
这样的教学,学生只能认识“3的倍数”,并不能理解“3的倍数的特征”的深层含义。在教学时,教师若出示图5,让学生将每个计数单位连续拿出3,就会发现1个十里有3个三,余1个,几个十就会余几个三;1个百里有33个三,余下1个,几个百就会余几个三。于是,把所有数位上的“零头”与个位上的方块数合在一起,如果和是3的倍数,那么整个数就是3的倍数,反之就不是。教师用直观的图形引导学生深刻领悟“3的倍数的特征”,这样既帮助了学生探寻规律背后的原理,又提高了学生的几何直观能力。
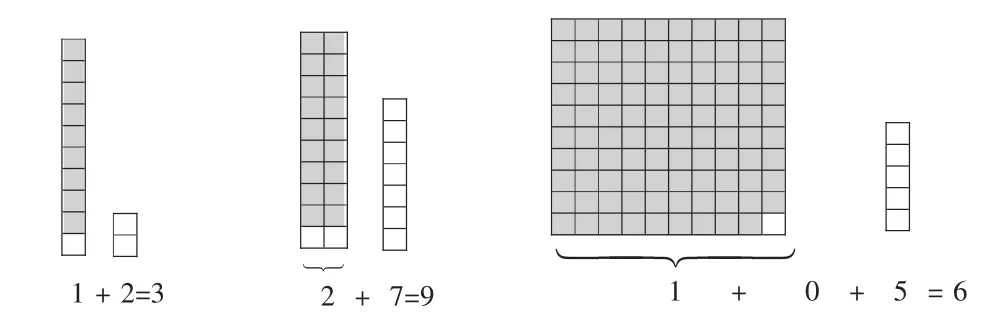
图5
三、构图,数形结合巧解题
在解决一些数学问题时,构图越巧妙,几何特征越明显,解决问题就更有效。通过构图,既能将问题直观地呈现出来,又能精准地刻画数学本质,而抓住了数学本质,就可以冲破定式模式的束缚,找准解题方法,实现解题优化。
例如,对于练习题“1+3+5+7+9+11+…+99”,教师不妨引导学生通过构图(如图6)来分析。

图6
学生通过构图可以找出规律“n个连续奇数的和等于n的平方”,在此基础上推理出:1+3+5+7+9+11+…+99中有50个奇数,因此结果为502,即2500。
通过构图来解题有两个好处。一方面,几何直观的实用性和重要性得以彰显,不仅打开了解题入口,而且降低了解题难度;另一方面,学生根据题意构图的能力得到锻炼,几何直观能力得到提升。
总之,几何直观对于学生的数学学习起到了极其重要的作用。在教学中,教师应深入研究几何直观的内涵,指导学生用图、造图、构图,掌握运用几何直观解题的方法,从而提高学生的数学素养和解题能力。

