“扇”分点“火”
——以“扇形统计图”为例谈过程性目标的落实
浙江宁波市鄞州区云龙镇甲南小学(315135) 陈志军
数学课程标准明确了义务教育阶段数学课程的总目标,并从知识与技能、数学思考、解决问题、情感与态度等四个方面做出了进一步的阐述。可见,课程标准对教学目标的落实不再是单一的“双基”,教师应注重过程性目标的落实。过程性目标的落实是要让学生通过经历(感受)、体验(体会)、探索,从而发现研究对象的特征及与其他对象的区别和联系。下面我结合“扇形统计图”的教学来谈谈过程性目标的落实。
[案例描述]
教师通过情境引入复习条形统计图和折线统计图的特点后,和学生进行如下交流。
师:现在老师在这个统计表中加上一列。(课件出示“占全班人数的百分之几”这一列)这一列表示什么?
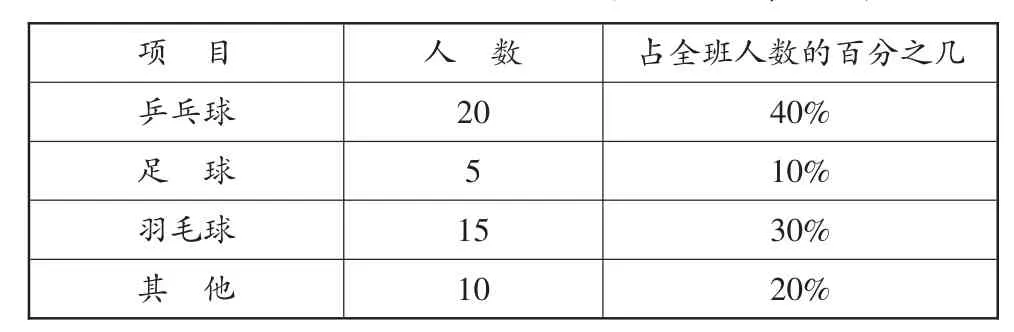
项 目 人 数 占全班人数的百分之几乒乓球 20 40%足 球 5 10%羽毛球 15 30%其 他 10 20%
生1:表示喜欢乒乓球的人数占全班人数的百分之几。
师:你能分别说一说吗?(学生一一解释四个百分数的含义)
师:把这样的四个百分数加起来就是多少呢?
生2:100%。
师:现在用条形和折线统计图还能表示喜欢各个项目的人数占全班人数的百分之几吗?
生3:不能。
师:看来我们需要一种新的统计图。请同学们拿出练习纸,试着把表示各个项目占全班人数的百分之几在圆中(如右图)表示出来。

(学生独立完成,教师巡视指导并收集素材,反馈成果)
师:你是怎么想的?什么是扇形?每个扇形表示什么?圆表示什么?(板书:扇形,圆)
生4:扇形的面积占圆的面积的40%,即表示喜欢乒乓的人数占全班人数的40%;扇形的面积占圆的面积的10%,即表示喜欢足球的人数占全班人数的10%;扇形的面积占圆的面积的30%,即表示喜欢羽毛球的人数占全班人数的30%。
师:同学们想的和数学家想的一模一样,这就是扇形统计图。(板书课题,同时课件出示标准的扇形统计图)
师:这个“40%”表示什么?所有百分数加起来的和是多少?
生5:100%。
师:你是怎么想的?不计算就能知道的吗?
生6:这个扇形统计图是把全班人数看作“1”,也就是100%。
师:像这样用整个圆表示总数(单位“1”),用圆内各个扇形的大小表示各部分数量占总数的百分之几的统计图就是扇形统计图。
师:光从这个扇形统计图中你能直接看出喜欢足球的有几人吗?
生7:不能。
师:那扇形统计图是表示什么的?
生8:表示各部分数量与总数之间的关系。
师:若601班共有50名学生,你能通过计算知道喜欢足球的有几人,喜欢羽毛球的有几人吗?(也可让学生选择自己喜欢的两个问题进行计算)
师:现在601班的班主任要去购买体育器材,你有什么想跟他说的吗?
生9:多买些乒乓球,少买些足球,因为喜欢乒乓球的人数多,喜欢足球的人数少。
[体会与思考]
一、星星之火——经历(感受)
“经历”(感受)是指让学生在特定的数学活动中,获得或感知一些初步的经验。初步感知是儿童认知水平发展的最低层面,但如果跳过初步感知的阶段,直接让学生去体会、去探索事物,那么就违反了学生的认知发展规律。大多数学生将无法理解或难以接受,随着时间的冲淡,遗忘的速度也会加快。因此,在上述案例的教学中,教师先在情境中复习了条形统计图和折线统计图的特点后,制造了一个知识的冲突——在统计表加上一列(包含百分数知识),此时用条形统计图和折线统计图就不能再表示出统计表中的数据,就需要创造一种新的统计图——扇形统计图。由于学生身临其境地感受到用条形统计图和折线统计图是无法表示出谁是谁的百分之几,就会去创造新的统计图。在经历知识的冲突中,学生就能初步感受到扇形统计图的特点,同时也留下了想象扇形统计图的空间,为下一个层面的体验找到了起点。
二、积薪之火——体验(体会)
“体验”(体会)是指参与特定的数学活动,在具体情境中初步认识对象的特征,获得一些经验。“体验”所要获得知识和经验是建立在经历的基础上的,也就是在初步认识了某种事物后再经过特定的活动,从而进一步了解事物,体会它存在的作用及必要性。“体验”这一环节是学生感受对象循序渐进的重要环节。因此,要让学生充分参与活动,深入体验事物的来龙去脉,从中获取比较深刻的知识和经验。在上述教学案例中,待学生初步感知扇形统计图的作用后,教师安排了一个动手创造扇形统计图的环节(教师给学生准备的圆已经画好了圆心和十等份点,能给学生很大的启发)。大多数学生通过思考都能在圆里表示出相应的百分数,在展示自己的作品时,也能说出自己的想法。学生通过画扇形统计图,能真正体验到扇形统计图的本质,也能在动手操作的数学活动中体验到成功的喜悦。
三、燎原之火——探索
“探索”是指让学生主动参与特定的数学活动,通过观察、实验、推理等活动发现对象的某些特征或与其他对象的区别与联系。这一环节是学生了解、理解、掌握知识本质的重要环节。它所研究的事物或知识是建立在“经历”和“体验”两个层面之上的,是研究事物或知识的本质。学生在进一步感知了知识的特征后,还需要探索知识的本质。此时,教师应设计特定的环节让学生去观察、推理,从而挖掘知识的本质,更好地理解和掌握知识。上述案例中,在学生动手操作设计扇形统计图之后,教师让学生去观察分析这个扇形统计图:扇形表示各部分数量,整个圆就表示总数(单位“1”),扇形统计图表示部分数量和总数之间的关系。通过动手操作绘制扇形统计图,动脑去分析扇形统计图的本质,学生对本课知识的理解和掌握程度又一次得到了提高。最后,让学生推理什么器材可以多买点,什么器材可以少买点,不但巩固了本课知识,还培养了学生的看图能力,发展了学生的推理能力。
总之,如何帮助学生去感受知识产生的必要性,体验知识形成的过程,探索知识的本质,是数学课堂教学中落实过程性目标的关键。作为教师,要抛弃“灌输式”教学模式,要让学生成为学习的主人,从不同的角度和途径给学生搭建学习平台,使每一位学生都成为“经历者”“体验者”和“探索者”。
———《扇形的认识》教学廖

