2017年全国卷Ⅱ理科23题的多解及推广*

(641100)

1.试题及评价

试题(2017年全国卷Ⅱ理科第23题)已知a>0,b>0,a3+b3=2，证明：

(Ⅰ)(a+b)(a5+b5)≥4；

(Ⅱ)a+b≤2.

试题简评：试题具有一定的难度、深度和广度，呈现十大亮点：形式优美、构思巧妙、叙述简洁、通俗易懂、不偏不怪、解法多样、内涵丰富、数学味浓、不设陷阱、可一般化.这些亮点完全包含了数学家匈菲尔德在1994年提出一道好的数学题应具备五个要求：“容易接受的、一题多解、蕴含了重要的数学思想、不故意设陷阱、可推广和一般化.”因此，该试题是一道好的高考试题.

2.解法深究

“问题是数学的心脏”．美国数学家P.R.Halmos指出“数学家存在的主要理由是解问题，数学的真正组成部分是问题和解”．在数学活动中，数学问题是数学研究的对象，解决问题不仅是数学研究的目标，同时也是数学活动的最基本形式和主要内容.正如G.Bolya在《数学的发现》序言中所说“中学数学的首要任务就是加强解题训练”，“掌握数学就意味着善于解一些要求独立思考，思路合理，见解独到和有发明创造的题．”由此可见，解题研究在数学活动中占有十分重要地位．本文案例是解题研究的良好素材，解答视角宽，方法多样，能帮助学生通过有限的解题研究领悟那种能解无限道题的数学机智.(罗增儒语)

2.1 (Ⅰ)的解法研究

(Ⅰ)的解答视角如下：

视角1 重要不等式法

(1)a2≥0

方法1：(a+b)(a5+b5)=a6+ab5+ba5+b6=(a3+b3)2+ab(a4+b4-2a2b2)=4+

ab(a2-b2)2≥4，当且仅当a=b时，“=”成立.

(2)基本不等式

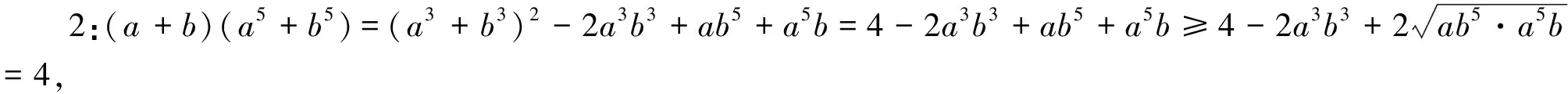
(3)柯西不等式

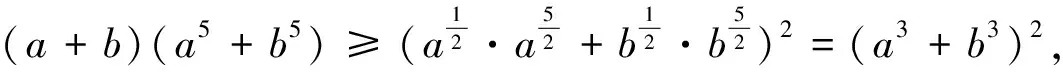
视角2 向量法

视角3 判别式法

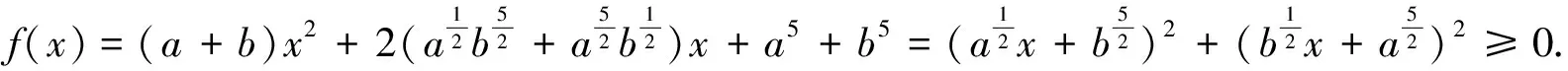
视角4 设参法

方法6：令a=kb(k>0)，(a+b)(a5+b5)=(k6+k5+k+1)b6=(k6+2k3+1)b6+(k5-2k3+k)b6=4+k(k2-1)2b6≥4，当且仅当k=1，即a=b时，“=”成立.

方法7：由a3+b3=2，得

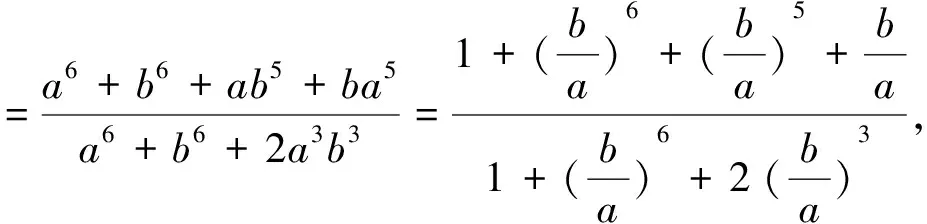
(a+b)(a5+b5)≥4.

2.2 (Ⅱ)的解法研究

(Ⅱ)的解答视角如下：

视角1 重要不等式法

(1)基本不等式及变式

方法1：由a3+1+1≥3a，b3+1+1≥3b，得a3+b3+4≥3(a+b)，因为a3+b3=2，所以a+b≤2，当且仅当a=b时，“=”成立.

方法2：因为a3+b3=2，所以a3+b3=(a+b)3-3ab(a+b)≥(a+b)3-

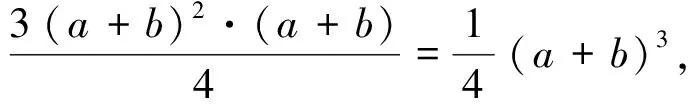
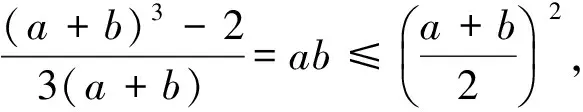
(2)柯西不等式推广

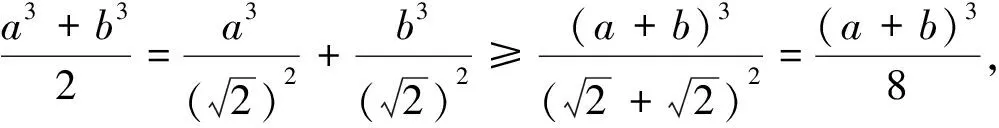
(3)幂平均不等式

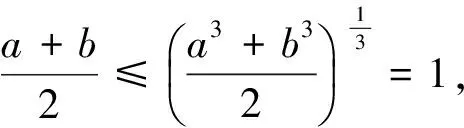
(4)Jensen不等式

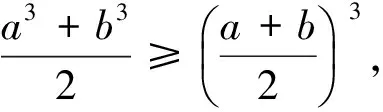
视角2 判别式法

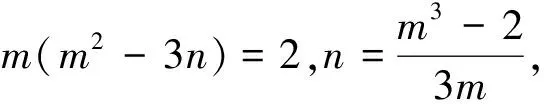
视角3 参数法

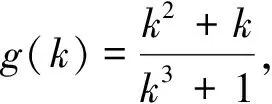
视角4 导数法

3.试题的推广

数学推广是指在一定范围内或一定层次上对数学概念、定理、法则进行拓展，使之在更大范围或更高层次上成立，此外，也指对条件、结论进行结构分析以后，进行适当变化，使得到的新命题为真.张景中院士指出：“推广是数学研究中极其重要的手段之一，数学自身的发展在很大程度上依赖于推广.数学家总是在已有知识的基础上，向未知的领域扩展，从实际的概念及问题推广出各式各样的新概念、新问题.” 推广的一个好处是对信息的整理，几个密切相关的事实被整合到一个更宽广的体系之内． 对本文中问题进行推广，可以更加清晰地揭示出问题的本质.

3.1 (Ⅰ)的推广

视角1 推广问题条件的次数、系数及结论次数

推广1 已知a,b,m,n,p,q,s,t,w>0,sam+tbw=n，则(sap+tbq)(sa2m-p+tb2w-q)≥n2.

视角2 推广问题的条件系数、元的个数及结论次数

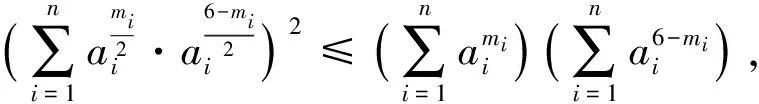
视角3 推广条件的次数、系数和元的个数及结论次数

3.2 (Ⅱ)的推广

视角1 推广条件的次数、系数

推广1 已知a,b,s,t,m,w,n>0,sam+tbw=n，则msa+wtb≤n+(m-1)s+(w-1)t.

视角2 推广元的个数、次数

本文是研究高考试题解法和推广的一个典型案例，需要指出的是文中的部分解法和推广可以直接纳入课堂教学，但不宜全部进入课堂教学.同时，高考试题研究还有很多视角，本文的研究权作抛砖引玉.