两个优美代数不等式的证明

陕西省绥德县绥德中学 (718000) 王 炜

安振平老师在文[1]中提出了四十个优美不等式，本文将给出第(1)个优美不等式和第(11)个优美不等式的证明.

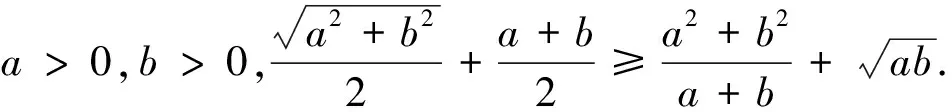
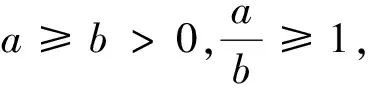
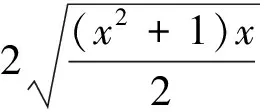
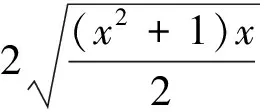
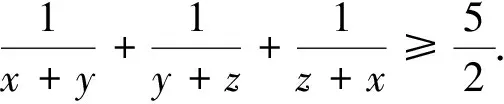
证法一：设s=x+y+z,p=xyz,q=xy+yz+zx,由题知p+q=1,由恒等式(x+y)(y+z)(z+x)=sq-p=s(1-p)-p,知左端通分后分母为s(1-p)-p,我们再考虑化简分子，即化简表达式∑(x+y)(y+z),∑(x+y)(y+z)=∑[y2+(x+z)y+xz]=∑x2+∑(s-y)y+∑xz=s∑y+q=s2+q=s2+1-p，只需证2(s2+1-p)≥5[s(1-p)-p],它等价于p(3+5s)≥-2s2+5s-2,①

综上所述，原不等式成立.

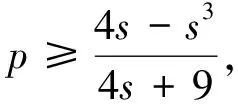
综上所述，原不等式成立.