一种基于断面高程数据的河道冲淤计算方法—曲线正交网格地形法*

孙中强，谷 硕，王厚杰，3，杨作升，3，毕乃双，3**

(1.中国海洋大学海底科学与探测技术教育部重点实验室，山东 青岛 266100； 2.黄河水利委员会，水文局，河南 郑州 450004；3.青岛海洋科学与技术国家实验室，海洋地质过程与环境功能实验室，山东 青岛 266061)

河道冲淤演化是河流径流与泥沙相互作用的结果，是河流稳定与安全的关键指标，也是河流治理与规划的重要参考依据。同时，作为陆源物质与能量向海洋传输的关键通道，河道的冲淤演化也关系到关键元素的地球化学循环和物质的源汇过程。目前，传统的河道冲淤研究手段包括基于水文站水文泥沙观测数据和河道地形高程测量的定量计算，即输沙量法和断面法[1-4]。

输沙量法也称输沙量平衡法、输沙率法，是利用水文站实测水沙资料以及区间增沙、引沙资料进行计算的[2-3]。输沙量法不需要考虑河道地形演变，且水文站测验时间间隔较小、资料连续，对于事件性水沙过程对河道冲淤变化的影响[5,6]具有较好的指示意义。早在1950年，Einstein就建立了均匀沙推移质输沙率统计公式[7]，1955年Colby等人提出了根据部份实测资料计算全沙输沙率的方法[8]。然而1956年钱宁等人基于悬沙理论提出了悬移质积点测量决定输沙率时会引起误差的问题[9]，此后国内外众多学者就河流输沙率的修正计算进行了大量研究[2,10-14]。但是，这些计算方法多具有所需参数多、过程复杂、普适性差等缺点，在一些河道变迁频繁或缺少历史资料的情况下不能较好的广泛应用。另外，输沙量法计算存在缺少推移质输沙数据、未考虑水量不平衡和区间引水引沙资料不全面等缺陷，长期计算结果存在普遍失真现象[15]。

断面法又称断面地形法，是利用断面地形实测资料，按照固定滩槽和间距的梯形体或锥体进行计算的[2-4]。前人研究表明，断面法冲淤计算值仅与始末状态有关，不存在输沙量法的累积性误差问题，且相对误差随河道累积冲淤量的增加误差还会逐渐减小[2]；对于小范围顺直河段的计算，断面法基本上可以反映河道实际冲淤情况[16]；而对于大范围且河弯曲折的情况，则需在弯道、汊道、河道急剧放宽和束窄的局部河段布置相对较密的断面[4]。由于断面法计算仅用到断面和断面间距数据，其计算精度取决于实测数据的精度和断面的密度，结果相对较粗略[17]。

随着河道治理对于河道冲淤演化要求的提高，传统方法已渐渐不能满足实际工作中对计算精度和空间分辨能力的需求，网格地形法应运而生。网格地形法是近年来随着计算机技术以及遥感技术发展出现的一种新的河道定量冲淤计算方法，是基于卫星遥感数据和野外实测河道地形三维数据，建立河道数字高程模型(Digital Elevation Model, DEM)进行河道冲淤计算的[4,16]。该方法不仅能够进一步提高计算结果精度，而且拥有较强的空间分析能力，计算结果的可视化效果更加直观，具有较好的应用前景。

得益于近年来卫星遥感技术的迅速发展，国内外一些机构(美国宇航局(NASA)、德国宇航中心(DLR)等)逐渐开放了全球陆地高程卫星遥感数据，分辨率也相当可观。然而，受水面波动、悬沙浓度、温盐变化等因素的影响，水下高程数据仍主要依靠野外实地测量获得。河道固定断面测量工作开展较早，发展成熟，数据相对完善，是研究地貌演化常用数据。部分国内外学者就河道地形模型建立中的网格选取与生成[18]、断面数据插值算法[19-21]、模型体积计算[17]、与遥感数据耦合[22]以及实际计算模拟应用[1,23]等方面做了大量研究，并取得了显著的成果。前人应用网格地形法进行河道冲淤演化研究中为了保证计算结果的准确性，往往需要大量的河道地形数据作为支撑，对断面数据的要求也较高。但是，由于野外测量实际条件的限制，进行长期、大范围、高密度的野外测量工作并不可行。特别是早期河道断面地形测量工作中，断面间距、方位变化往往较大，导致断面数据非常有限而且横纵向分布极不均匀。如何利用有限的实测断面数据结合卫星遥感数据进行河道冲淤计算，成为现阶段网格地形法急需解决的难题。

本文基于河道断面高程数据和遥感数据，提出了一种基于DEM进行河道冲淤定量计算的普适方法，并以黄河下游部分河道为例，比较了本文方法和一般网格地形法、断面法的计算结果差异，并对导致这一差异的主控因素进行了讨论分析。

1 研究区域概况

黄河以水少沙多、水沙异源著称，历史上其年均向渤海输送泥沙量高达10.8亿t[24]，位于世界大河第二位。黄河下游地势低平开阔，河道宽浅，大量泥沙淤积，使得河床抬升，形成著名的地上悬河，决口与改道频发[25]。近年来由于自然因素以及人类活动的影响，黄河水沙量急剧减少[26]，下游河道淤积加重。为缓解下游河道淤积，提高河道行洪能力，黄河水利委员会自2002年利用小浪底等干流大型水库在汛期开展调水调沙工作[27]。此后，下游河道持续淤积状况改善，河床冲刷明显[28-30]。

研究区(见图1)位于黄河下游，本文选取了孙口-艾山河段，孙口-艾山河段位于孙口、艾山水文站之间，长约63.9 km，落差约7.5 m，河道曲折。

图1 研究区地形及断面分布Fig.1 Topography and settings of bathymetrical cross sections in study area

2 数据与方法

2.1 数据来源

本文计算所用数据包括河道断面高程数据以及卫星遥感数据。断面高程数据为1991年10月—2012年10月黄河水利委员会统测黄河下游断面高程数据(不包括1998年以后加密断面)，孙口-艾山段共有固定断面17个，断面间距2～9 km。卫星遥感数据为Landsat5的TM遥感影像数据，由美国地球资源与科学中心免费下载(http://glovis.usgs.gov/)，分辨率为30 m，其被广泛应用在地形地貌研究。本文选取1991—2012年每年10月前后与断面数据测量时间最为接近的无云或少云遮挡的研究区遥感影像数据。

2.2 计算方法

2.2.1 断面法 断面法计算具体公式如下：

(1)

(2)

式中：为i～i+1横断面间河槽体积；为第i个横断面面积；为i～i+1横断面之间间距，两测次河槽体积之差即为断面间冲淤体积。对于任意相邻两断面i、j，当且时，应用(2)式[17]进行计算。

2.2.2 基于矩形网格建模的网格地形法 本文矩形网格计算基于Surfer11.0软件完成，该软件是美国Golden公司开发的地学常用绘图软件之一，其内置多种常见插值方法，同时可以对生成的网格模型进行体积计算，具有方便、快捷、安装简单等特点，常用于数据相对充足且空间分布均匀的海洋或湖泊DEM的建立。建模具体步骤如下：(1)提取断面测点空间三维坐标。将测点坐标用Global Mapper软件统一转换为基于高斯克吕格投影的WGS84坐标系。(2)将测点高程数据直接插值并网格化，得到数字高程模型。Surfer软件直接建模生成网格为规则矩形网格，考虑断面数据实测间隔、提取的河道边界精度，为了使模型网格尽可能贴合河道边界，计算用网格间距为30 m；由于断面数据空间分布差异较大且外插数据不可靠，插值方法采用结果较为准确的三角网线性插值。(3)计算网格模型体积变化，即为河道冲淤体积。

2.2.3 基于曲线正交网格的网格地形法 本文提出了一种应用断面数据和卫星遥感数据，建立基于曲线政教网格的DEM计算河道冲淤的方法，具体步骤如下：(1)提取研究区河道边界。本文选择对水陆边界最为敏感的波段4、5、1(RGB)合成Landsat假彩色图片，应用Global Mapper软件获取历年与断面数据测量时间对应的河道研究区边界，河道固定断面处以断面法固定滩槽界位置控制，并勾画研究年限内总体河势方向线。(2)根据河道边界建立DEM网格。考虑河道蜿蜒、曲折多变，规则矩形网格不能准确表示河道边界的变化(见图2a)，本文选用与河道边界更为贴合的曲线正交网格(见图2b)。网格间距一般不超过30 m，最大为100 m。(3)断面数据插值建模。应用自编Matlab程序首先按照反距离插值法将实测断面高程数据插值到垂直于主河道方向的网格控制点，再沿河道河势方向按河长逐行进行线性内插，得到河道DEM(见图3)。(4)模型体积计算。使用自编Matlab程序计算模型空间体积，模型体积变化即为河道冲淤变化体积。如图4，DEM中x-y平面任意三个相邻点(A，B，C)对应的五面体(ABC-DE′F′)的体积等于三棱柱(ABD-DEF)的体积减去五面体(D-EFF′E′)的体积，即

(3)

其中：AD为最长棱，可通过排序赋值得到；DD′为D到EF的高。

((a)规则矩形网格Rectangular grid; (b)曲线正交网格Orthogonal curvilinear grid.)
图2 不同网格贴合河道边界示意图
Fig.2 Two different DEM grids

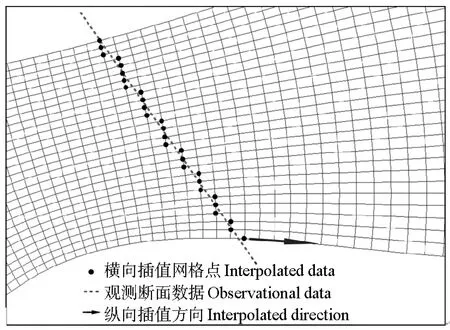
图3 基于曲线正交网格的断面数据插值示意图Fig.3 Schematic diagram of interpolationin calculation domain based on orthogonal curvilinear grid

图4 DEM体积计算示意图Fig.4 Schematic diagram for volume calculation of DEM

3 不同模型冲淤计算结果

孙口-艾山河段主河道的冲淤计算结果表明三种方法计算结果冲淤性质基本一致，但冲淤数量存在明显差异，尤其是矩形网格建模与本文方法和断面法差异显著(见图5)。研究区主河道整体呈先淤后冲趋势：除1993、1996和1998年出现冲刷外，至2000年10月研究区呈持续淤积，单次最大淤积出现在1997年；此后研究区呈持续冲刷，2004年10月与1992年10月冲淤水平基本相当，2012年10月达最大冲刷，单次最大冲刷出现在2003年。

结合相关性分析(见图6)和误差分析(见表1)可以看出，矩形网格建模和断面法的累计误差随累计冲刷量增大而增大，矩形网格建模计算误差更大。矩形网格建模较本文方法计算结果明显偏小，两者拟合直线斜率仅为0.62，线性正相关性较好；两者绝对误差范围为(-5.91～4.76)×106m3，平均绝对误差约为0.68×106m3，相对误差范围可达-157.3%～56.7%，平均相对误差高达-40.7%。断面法计算结果总体较本文方法略有偏大，两者线性拟合斜率为1.09，呈高度线性正相关，但绝对误差范围为(-1.05～1.35)×106m3，平均误差为-0.15×106m3，相对误差范围高达-71%～45%，平均相对误差约为9.0%。

(正值表示淤积，负值表示冲刷。Positive values indicate accumulation, and negative values indicate erosion.)
图5 孙口-艾山主河道累计冲淤曲线
Fig.5 Cumulative erosion-accumulation sediment volume in main channel between bathymetrical cross sectionsSunkou and Aishan

图6 计算结果相关性分析Fig.6 Correlation analysis of calculated erosion-accumulation sediment volumes using different methods

表1 1991年10月～2012年10月孙口-艾山段主河道冲淤体积计算结果Table 1 Erosion-accumulation sediment volume in main channel from October 1991 to October 2012 between bathymetrical cross sections Sunkou and Aishan

注：1绝对误差=断面法或矩形网格法-本文方法；2相对误差=(断面法或矩形网格法-本文方法)/本文方法。
Note:1.Absolute error=Gross-section or Method using rectangulargrid-Method in this paper; 2.Relative error=(Gross-section or Method using rectangulargrid-Method in this paper)/Method in this paper.

4 讨论

本文方法充分考虑了河床地形的复杂多变情况，从卫星遥感图片提取河道边界，使用更好适应性的曲线正交网格，能够很好的重构复杂多变的河道形态。对于河道地形变化横向插值时仅使用插值点最近两个点的断面数据，保证了插值结果与断面数据的高度一致，降低了断面方位变化对插值结果的影响(见图7)。此外，用曲线正交网格的河流中泓河势方向作为模型的插值方向，符合河道地形的纵深变化，采用线性内插进行纵向插值，保证了网格点数据只受上下两断面数据影响，能够利用有限的断面数据较为准确重构河道地形(见图8a)。

(a.垂直断面(邵庄)Perpendicular section(Shaozhuang)； b.斜交断面(孙口)Oblique section(Sunkou).)

4.1 矩形网格建模的误差原因分析

矩形网格建模与本文方法误差较大，其原因是河道断面高程数据空间分布极不均匀，相邻两固定断面间隔较大(2～9 km)，数据点对网格控制明显不足(见图8b)。直接插值计算地形高程与距离的关系时，使用的是点与点之间的直线距离L1(见图8b)。实际上，河道地形高程是点与点沿平行或垂直主河道主流河势方向距离河长L2的函数，对于河弯曲折的河段L1明显小于L2，使插值结果与实际河道情况不符，得到的河道地形模型有明显的不连续条带。此外，在对河道边界外部区域的插值数据进行剔除的过程中，只有部分DEM数据参与计算，会导致结果进一步偏小。因此，导致基于矩形网格的计算的河道冲淤量显著小于断面法和基于曲线正交网格法(见图5)。

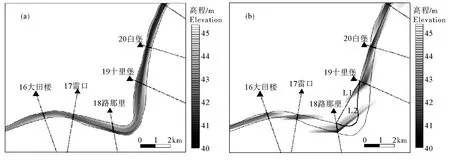
(a.本文方法建模This study； b.矩形网格建模Model using rectangulargrid.)图8 不同方法建模结果高程图Fig.8 Modeling resultsbased on different methods

4.2 断面法的误差原因分析

断面法与本文方法计算结果总体较为接近，孙口-艾山河段断面法计算河道冲淤量较本文曲线正交网格地形法平均高约9%，但个别年份相差可达71%(1997—1998年)(见表1)。断面法主要基于断面面积变化和断面间距进行冲淤计算，并假设断面间河道宽度无明显变化以及断面方位与河道基本垂直。然而，受自然和人为因素的影响，实际河道宽度沿程变化显著且不均匀和随机性较强，河道宽度最小约为250 m，最大可达650 m(见图9)。断面法仅使用有限的断面测点高程数据以及断面间距数据，将河道地形简单的使用梯形体或者截锥表示，其结果强烈依赖于断面代表性，存在一定的偶然性，无法准确精细的刻画河道地形的演变，导致断面法与本文的曲线正交网格法存在一定的差异。此外，由于黄河径流量和泥沙含量年际和季节性变化较大，自然状态下的河道易发生摆动，使断面方位与河流流向的夹角不断变化，这一现象在研究区普遍存在(见表2)。当观测断面与河流流向存在一定夹角时(，则观测断面长度、面积与实际断面长度和面积存在如下关系：

图9 研究区河道宽度变化Fig.9 Variation in the width of the river channel

(4)

其中：L为观测断面长度；l为实际断面长度，对应实际断面面积也为观测断面面积的sinα倍。断面法计算时没有改正角度引起的断面面积偏大，使得计算河槽体积也相应偏大，冲淤量也相应偏大(见表3)，这是导致断面法较本文方法偏大的另一因素。

随着河道治理与监测的不断发发展，河道断面密度不断增加。1998年以后黄河水利委员会对黄河下游淤积断面观测普遍加密，断面间距进一步减小，至2012年西霞院以下河段共有观测断面约370个，最小断面间距仅450 m。此外，随着科学技术的发展，野外测量的精度和遥感影像分辨率也在不断提高。这将会进一步提高构建河道DEM的精度，推进河道地形地貌演化研究及其机理研究和河道综合治理。

表2 研究区观测断面与河流流向夹角表Table 2 Average angle between bathymetrical cross section and the river channel in study area during 1991—2012

表3 1991年10月～2012年10月孙口-艾山断面与流向夹角校正结果Table 3 Angle correction resultsfrom 1991 to 2012 between cross sections Sunkou and Aishan

5 结论

(1)本文提出了一种应用河道固定断面测深资料和卫星遥感数据，基于曲线正交网格的河道数字高程模型(DEM)定量计算河道冲淤的普适方法，该方法不受河道形态和断面方位等因素的限制，能够利用有限的断面数据较为准确的构建河道DEM进行冲淤计算。

(2)以黄河孙口-艾山河段为例，分别应用本文方法、基于矩形网格的网格地形法和断面法进行冲淤计算，结果表明：基于矩形网格建模和断面法计算结果与本文结果趋势基本一致，但均存在明显误差。断面法计算结果与本文方法结果较为接近，平均相对误差约为9%，个别年份可达70%以上；基于矩形网格建模计算结果与本文方法结果相差较大，平均相对误差可达40%以上，最大误差超过157%。

(3)现有断面数据往往分布不均匀，对于弯曲河道的控制明显不足，是矩形网格建模计算误差的主要原因。而断面法计算误差主要由于未考虑河道宽度的沿程变化，仅基于断面面积和断面距离的梯形体或截锥计算河道冲淤变化。另外，由于河道长期摆动，断面与河流流向不垂直导致测量断面面积偏大，也是导致计算误差的主要原因。