基于波面起伏相关性估计海浪波长的新方法*
魏 来,管长龙
(中国海洋大学,山东 青岛 266100)
海浪是最常见的且与人类活动关系最密切的海洋波动。开展海浪的研究对于航运、造船、港口以及海上石油平台的建设有着十分重要的指导作用。同时,研究海浪对全球大洋的海气相互作用及气候变化也有着非常重要的意义。海浪的主要要素包括有效波高、波长、波周期等,其中有效波高及波周期可以通过单点测量的波面序列比较简便地得到[1],而波长的测量则较为复杂,原则上需要海浪波面起伏场的观测信息,然而现有的观测无法提供此种海浪场的完整信息,需要采用不同的近似方法,故成为众多海浪研究者关注的重要问题。在实际应用中,多采用间接测量方法,即根据有限水深中波浪的频散关系由波浪谱计算,而波浪谱的获得比较简单。Kirby等[2]提出了一种适用于整个水深范围的波浪非线性频散关系。李孟国[3]介绍了用波浪频散关系确定浅水波长的方法,讨论了水深、水流、波浪振幅对波长的影响。根据波浪谱间接计算波长的理论已经比较成熟,但需要假定波浪为线性、窄谱且受水深等因素的影响。因此,为了得到更精确、更可靠的数据,直接测量方法有着不可替代的作用。早期是通过目测直接估计波长,随着科技发展,卫星数据的增多,许多中外学者开始研究如何根据雷达或卫星图片分析大范围甚至全球波长分布。对海浪图像进行二维傅里叶变换寻找代表海浪主频率的极大点的位置,计算海浪的传播方向和波长是比较常见的方法。徐建华等[4]根据该方法从海浪图像灰度提取海浪波长及波向信息。孙京生等[5]根据该方法计算量大的缺点,提出了一维傅里叶变换法,提高了精度并减小了计算量。Tang等[6]提出了根据转动惯量法从图像中计算波长及波向的方法。陶法等[7]根据大量试验改进了二维傅里叶变换法,提高了抗噪性,解决了主频不明显的缺点。
使用卫星观测对于研究全球大洋波长分布有着十分重要的意义,具体到小尺度研究,却存在测量精度比较低及无法实时监测的缺点。因此,不少学者提出了一些适用于实验室[8]或外海小尺度观测的波长测量方法。冯驰等[9]提出了一种利用压力传感器反演波长的装置,该装置利用伯努利方程由压力计算水位变化得到波浪运动方程,并由此得到波浪的波数,最终根据波数计算波长。段春明等[10]及朱永强等[11]提出用一系列连续排列的测波仪测量一段距离内波面的变化来确定波浪形状,并由测波仪之间的距离计算波长的方法。冯越[12]提出了测量通过两个测波仪之间波浪的传播时间计算波速与波长的方法。上述方法理论上能够方便且有效的测量波长,然而在实际应用中还存在一些需要解决的问题。用一系列连续排列的测波仪会受到测波仪之间距离的影响。若距离太近会因为测波仪对波面的影响产生相互干扰;如距离太远会导致分辨率过低。实际海面的波浪是在不停变化,用两个测波仪测量波长需要解决准确测量通过两个测波仪之间时间的问题。基于以上问题,本文提出一种的新的可适用于实验室及外海测量的波长测量方法,该方法具有较高的精确度,且方便操作。
1 波长计算方法介绍
目前常用的波长测量方法分为以下几种:(1)根据有限水深中的波浪频散关系,通过波周期计算得到;(2)根据图像直接得到;(3)根据不同测波仪之间的相关关系计算得到。本文将主要采用第三种方法进行计算,并将第三种方法计算的结果与第一种方法进行对比。
1.1 根据频散关系计算波长
在小振幅波动理论假定下,有限水深中的波浪频散关系为:
ω2=gktanh(kd)。
(1)
其中:ω为波动的圆频率;g为重力加速度;k为波数;d为水深。而波动相速度与波长和周期的关系为:
(2)
其中:λ为波长;T为周期。将(2)式代入(1)式中得到:
(3)
(4)
由(4)式可迭代计算波浪波长。Guan等[13]曾提出一种直接由周期计算波长的半经验公式。
根据频散关系计算波浪波长是最方便的方法,而且在大部分情况下计算的结果与实测数据的误差都很小,然而该方法需假定波动振幅远远小于波长和水深,在实际海洋中并不总是满足该条件。实际的海浪往往是随机波的情形,被视为由许多具有不同波长和周期的组成波叠加而成。原则上(4)式仅适用于单个组成波,只在线性、窄谱的条件上才适用于随机波。
1.2 根据图像计算
根据图像计算波长对技术要求比较高。现有的方法有雷达测量或通过卫星拍照,已有许多学者提出了提取卫星图像反演波长的方法[14]。雷达测量海浪波长的原理是根据海面后向散射强度表征波峰,由于在中等入射角下,海面微尺度波为影响后向散射的主要因素,因此后向散射强度最大处并不位于波峰,而位于波峰前毛细波较多的地方[15],故雷达测量波长存在一定的误差。在实验室中亦可以用相机拍照,但照片中需要有参照物用以确定相对长度。同时,实验室中也可以用一系列排列紧密的测波仪来确定一段长度内的波浪状况,从而确定波长,这种方法实际上也是通过波浪的图像得到波长。然而在实际应用中,相邻的测波仪之间的间隔导致该方法的分辨率不高,在波长较短的时候该方法得到的结果误差较大;在波长较长的时候需要较多的测波仪才能得到一个完整的波长。
1.3 根据相关关系测量
波浪的相速度定义为波动传播的速度,因此可由波动通过两个测波仪的时间与两个测波仪的距离计算波速,再根据波速与波长的关系c=λ/T计算波长。
实际观测中海浪经常变化,如果两个测波仪之间相隔太远,会导致波形在两个测波仪之间发生变化,导致两个测波仪之间数据相关性较差。若两个测波仪相隔太近,会导致计算精度不够。例如,若两个测波仪之间间隔为5 cm,测波仪采样频率为100 Hz,此时波浪通过两个测波仪之间的时间为0.01 s的整数倍,计算得到的波速并不是连续的值。因此,提高波速的分辨率也是非常重要的工作。本文将采用样条插值及正弦函数拟合,提高波速的分辨率。其中,正弦函数拟合根据波面位移数据通过傅里叶变换,将其分解为一系列正弦函数的叠加,并选出其中振幅较大的部分相加得到波面位移的近似解析表达,并由此得到时间分辨率更高的波面位移时间序列。

表1 实验测量的8种不同情况的波浪Table 1 8 wave conditions measured in experiment /m·s-1
Note:①Without wind; ②With wind;③No mechanical wave;④1.6 Hz mechanical wave;⑤1.2 Hz mechanical wave(√为实验测量的情况。√ are measured conditions.)
2 计算结果对比
2.1 实验条件介绍
本文中使用的波浪数据由俄罗斯下诺夫哥罗德市的应用物理研究所中的风浪水槽中得到。实验室使用风机及机械造波器制造波浪。风浪水槽的长度为16 m,水槽中的水深为1.5 m,水温为290 K。波面位移数据用镍丝电阻式测波仪测量,测量采样频率为100 Hz,测量精度为0.1 mm。其中测波仪有三个,呈正三角形排列,边长为2.5 cm,其排列顺序如图1所示。由此可知波浪通过两个测波仪之间的传播的距离约为2.2 cm。
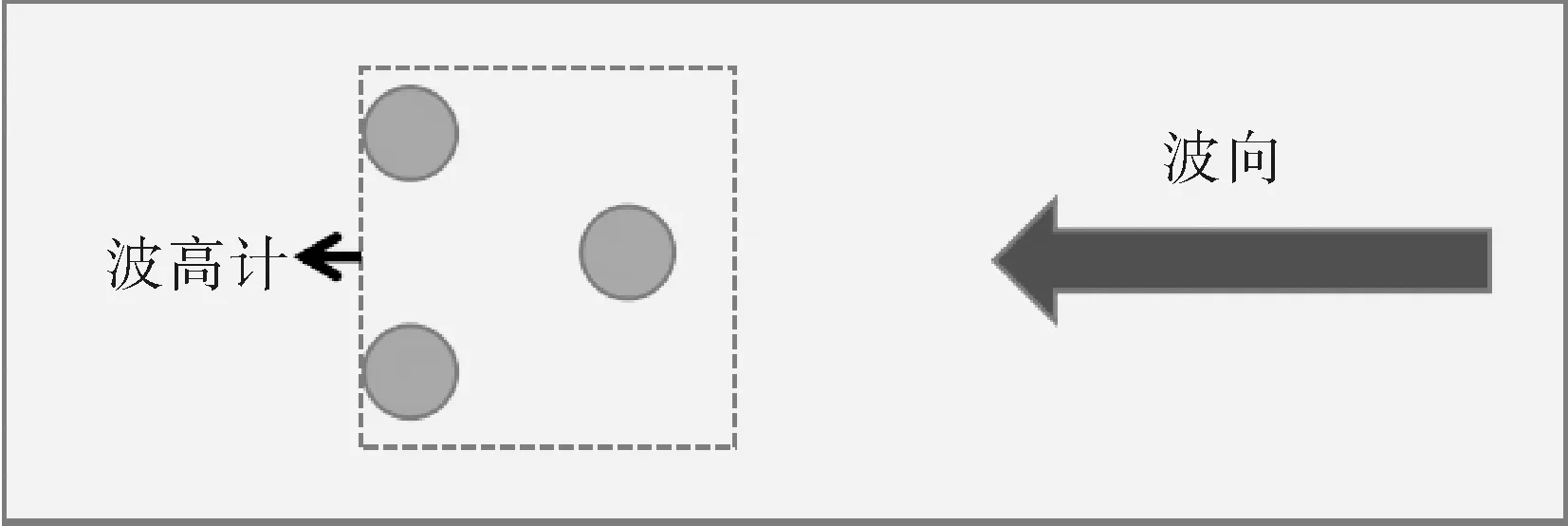
图1 测波仪在水槽中的排列俯视图Fig.1 Vertical view of wave gauges in wave tank
为了测试风浪与涌浪对本次实验使用方法的影响,实验将测量三种情况下的波浪:纯风浪、纯涌浪以及风涌混合浪。总共测量8种不同情况的波浪,其中纯风浪情况3种,纯涌浪2种,混合浪3种。具体测量情况如表1所示。为保证实验的准确性,每种波浪情况测量2次。
2.2 波浪状况分析
通过上跨零点法得到8种情况的波浪有效波高及谱峰周期结果如表2所示。
图2为根据1.2 Hz机械波+12 m/s风的波浪情况原始数据计算的两个测波仪之间的相关关系。由图可看出,相关关系在0.01及0.43 s有最大值。由0.43 s计算出的波速太慢,因此0.01 s为波浪通过两个测波仪之间的时间。而0.43-0.01=0.42 s为表3中对应该波浪情况谱峰周期的一半,证明了该方法的有效性。
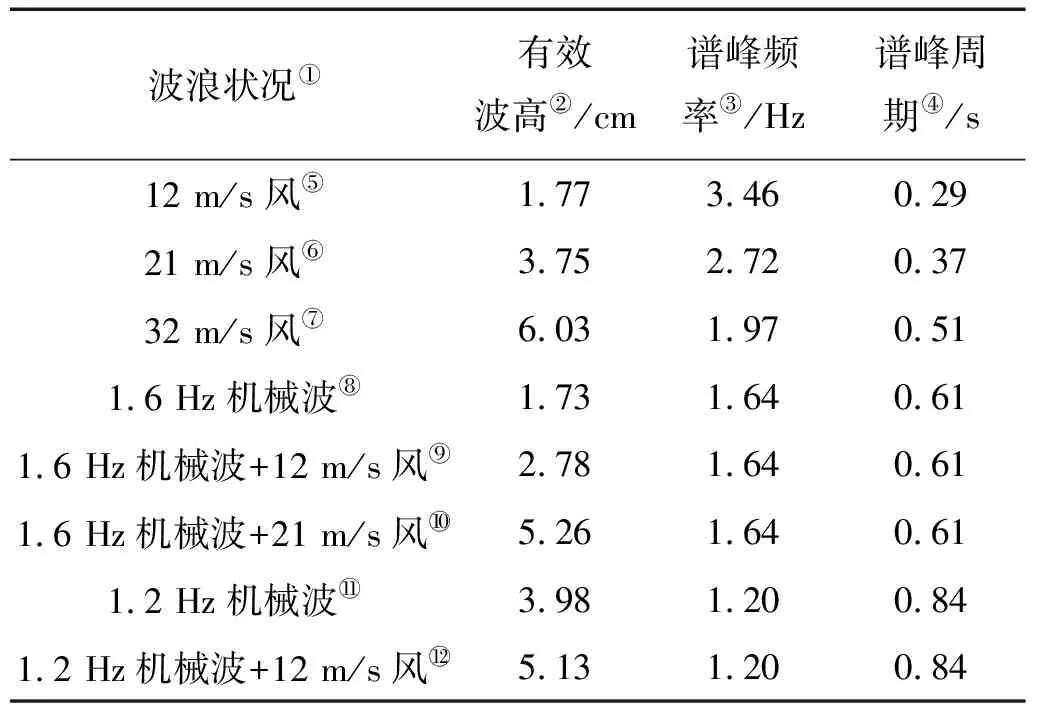
表2 8种波浪情况的有效波高及谱峰周期Table 2 Significant wave height and peak period of 8 measured wave conditions
Note:①Wave conditions;②Significant wave height;③Peak frequency;④Peak period;⑤12 m/s wind;⑥21 m/s wind;⑦32 m/s wind;⑧ 1.6 Hz mechanical wave;⑨ 1.6 Hz mechanical wave with 12 m/s wind;⑩1.6 Hz mechanical wave with 21 m/s wind;1.2 Hz mechanical;1.2 Hz mechanical with 12 m/s wind
2.3 插值计算
然而由以上方法得到的波浪在两个相邻测波仪之间传播时间分辨率太低,传播时间为0.01 s时两者的相关性最大,这说明传播时间在0~0.02 s之间,只能得到波动相速度大于2.165 1 m/s,分辨率偏低。为提高分辨率,本文利用MATLAB软件,采用样条插值及正弦函数拟合,由于样条插值效果较差,本文只使用正弦函数拟合,效果如图3所示。
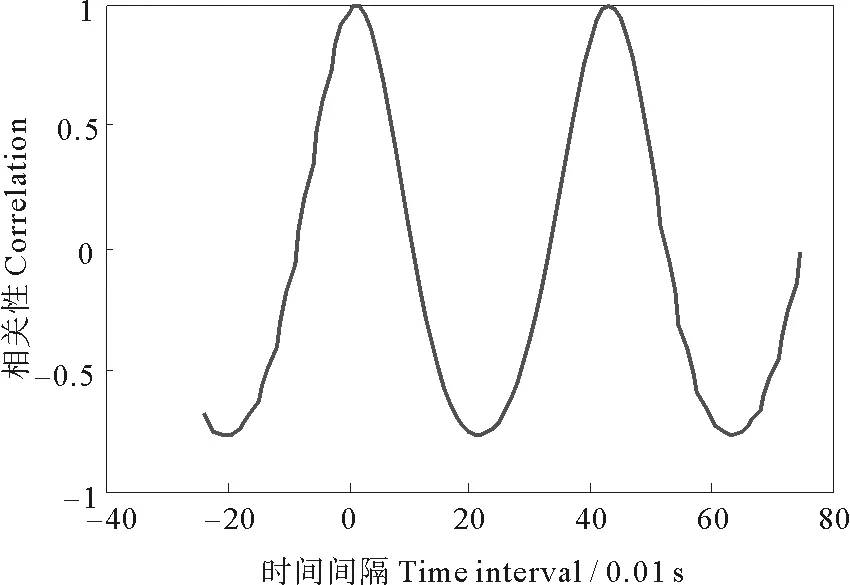
图2 两个测波仪数据的时间相关关系Fig 2 Time dependence of two wave gauge data
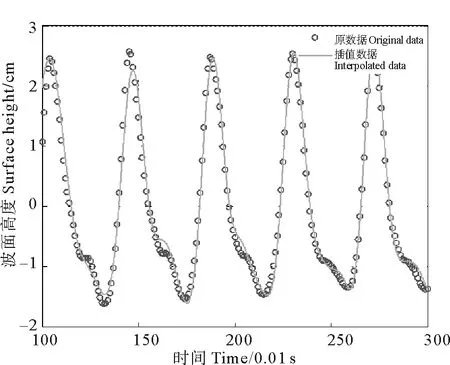
图3 插值后与原数据效果对比Fig 3 Comparison of interpolated data with original data
由图3可以看出,为了减少计算量,只选取总能量占95%的波动叠加,因此正弦函数对原数据的拟合效果在部分区间与原数据相比有一定的偏差,但总体上与原数据吻合。由于原数据分辨率较低,本文将采样间隔缩短至0.000 1 s(提高100倍分辨率),通过两个测波仪插值数据的相关关系计算,及两个相邻的测波仪的时间,计算每个波浪状况的波长,最终得到波长结果(见表3)。
由表3可以看出,两种方法得到的结果在波长较短时基本相同,随着测量波长的增加,由测波仪数据相关性测量得到的结果与通过频散关系计算得到的结果逐渐出现偏差。这可能是由于两个测波仪之间距离过近,在波长较长时,两个波高计之间的波浪占总波长的比例过小,使得拟合时有一定的失真。在实际测量时,对于波长较长的波浪应增大两个测波仪之间的距离,长波波形比短波更稳定,测量长波时增加测波仪之间距离并不会产生较大误差。
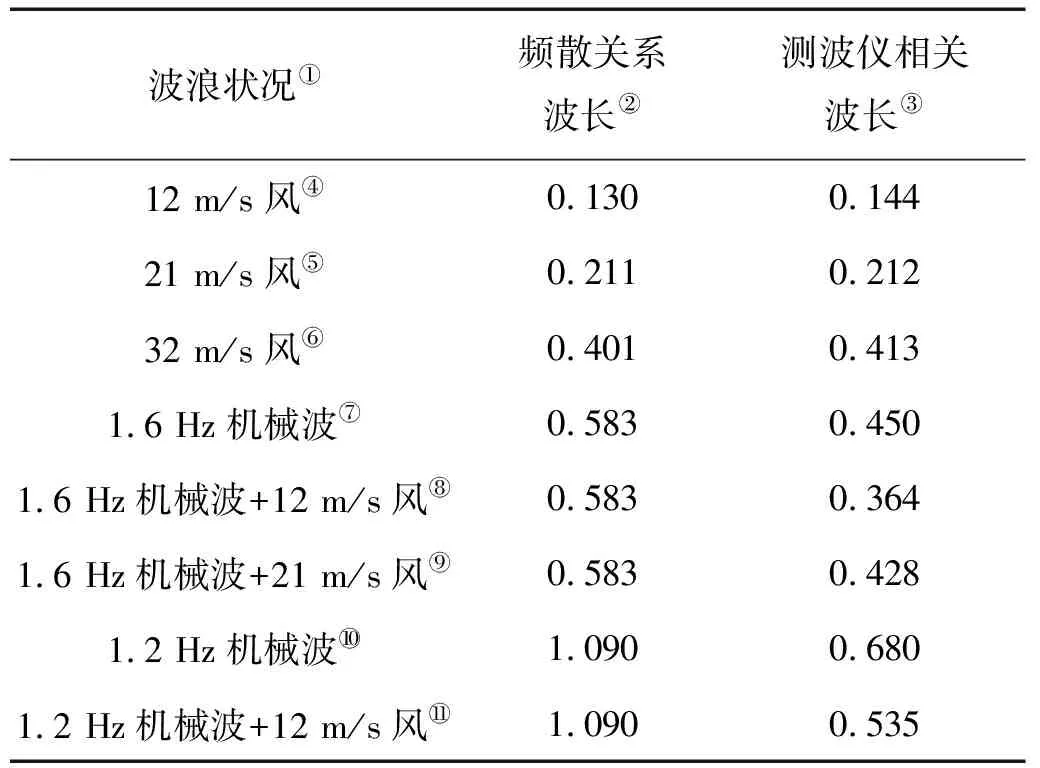
表3 两种方法计算得到的每种波浪状况的波长Table 3 Wavelength of each wave conditions calculated by two methods /m
Note:①Wave conditions;②Wavelength by dispersion retation;③Wavelength by corelation of wave gavge data;④12 m/s wind;⑤21 m/a wind;⑥32 m/s wind;⑦ 1.6 Hz mechanical wave;⑧ 1.6 Hz mechanical wave with 12 m/s wind;⑨1.6 Hz mechanical wave with 21 m/s wind;1.2 Hz mechanical wave;1.2 Hz mechanical with 12 m/s wind
对于混合浪,在纯风浪情况下12及21的风产生的波浪有效波高大于纯机械造波产生的波浪的有效波高。然而由于风浪的频谱能量不如涌浪集中,计算能量谱的时候,谱峰仍然为机械波(涌浪)的频率,由此导致由频散关系计算到的波长与纯机械波一致。而实际上,涌浪在谱峰频率的整数倍处从风浪中吸收能量。因此风浪涌浪之间的波-波相互作用使得波长由纯涌浪波长向纯风浪波长偏移,由测波仪相关关系法测量的结果可以很好的体现出这一点。因此,使用相邻测波仪相关关系计算波长是一种更好的方法。
3 总结与讨论
本文使用相邻测波仪相关关系计算了风浪、涌浪及混合浪波长并与传统的频散关系计算海浪波长的方法进行了对比。为了消除波浪传播期间波形变化导致的误差,实验中两个测波仪的距离较近,由原始数据计算得到的海浪波长分辨率较低。
为此,本文提出了一种提高分辨率的方法,利用快速傅里叶变换,将波浪数据分解为一系列正弦运动叠加,得到波浪运动的解析表达。在使用全部的正弦函数叠加时,得到的结果与原数据完全一致,然而这样的计算量偏大,在实际应用中,我们可以只选取占总能量95%或90%的部分进行计算,兼顾计算量与准确性。本文通过实验数据及对比实验验证了提出的方法的有效性和准确性。这一研究仍需要更多的实验数据支持。本次实验使用的测波仪位置固定,由于距离较短,虽然通过本文提出的正弦函数拟合提高了分辨率,但可能与实际波长还是有一定的差距,后期实验可以通过改变两个测波仪之间距离寻找最佳的距离。同时,在实验室实验中可以加入图像拍照法同步测量波长,对该方法结果进行对比验证。

