液压驱动并联加载机构正弦位置/力幅相控制

高长虹 何 彪 曲智勇 丛大成

(1.中航工业庆安集团有限公司航空设备研究所，西安 710077； 2.哈尔滨工业大学机电工程学院，哈尔滨 150001)

0 引言

近年来，随着液压伺服控制技术、并联结构理论和实时控制系统的发展，液压驱动并联加载机构作为对大型足尺试件进行大吨位、多自由度位置/力加载测试的重要加载设备，已被广泛应用于航空、航天、铁路、建筑等领域[1-7]。

正弦信号是加载机构常见的一种测试信号。由于受到液压系统非线性因素和试件耦合作用的影响，系统位置和力加载自由度的频宽难以提高，导致在对正弦位置/力加载信号跟踪时产生较大的幅值衰减和相位滞后[8-9]。为提高正弦信号的跟踪精度，学者们提出了许多不同类型的幅相控制策略，主要有基于Widrow-Hoff学习算法[9-14]、极值搜索技术[15]、在线辨识和迭代方法[16]等幅相控制策略。然而上述幅相控制方法多存在控制结构复杂、设定参数繁多、计算量大等问题，在控制参数整定过程中容易引起系统不稳定而造成对试件的破坏。为此，本文提出一种改进的幅相控制策略，通过评估正弦信号的幅值、相位和均值，将其作为控制变量并对各个变量通道进行单独控制，实现对正弦位置/力信号的精确跟踪。

1 改进的幅相控制结构及原理

任何一个正弦信号均可以被视为由幅值、相位、均值和频率4个特征参数组成。如果能够从给定和响应的正弦信号分离出这4个特征参数，那么就能直接对这4个特征参数进行控制。由于这4个特征参数互相独立、不存在耦合，故可以根据任务需要进一步实现对每个特征参数的独立控制。此外在使用给定频率的正弦信号激励系统时，响应信号频率不会变化，由于系统非线性因素的存在导致响应信号包含高次谐波频率分量而产生波形失真的情况，可通过谐波抑制技术[17]进行修正，不属于本文讨论范围。因此本文将响应信号的频率视为已知信息，不对其评估和控制。根据以上思想，提出图1所示的改进幅相控制结构。

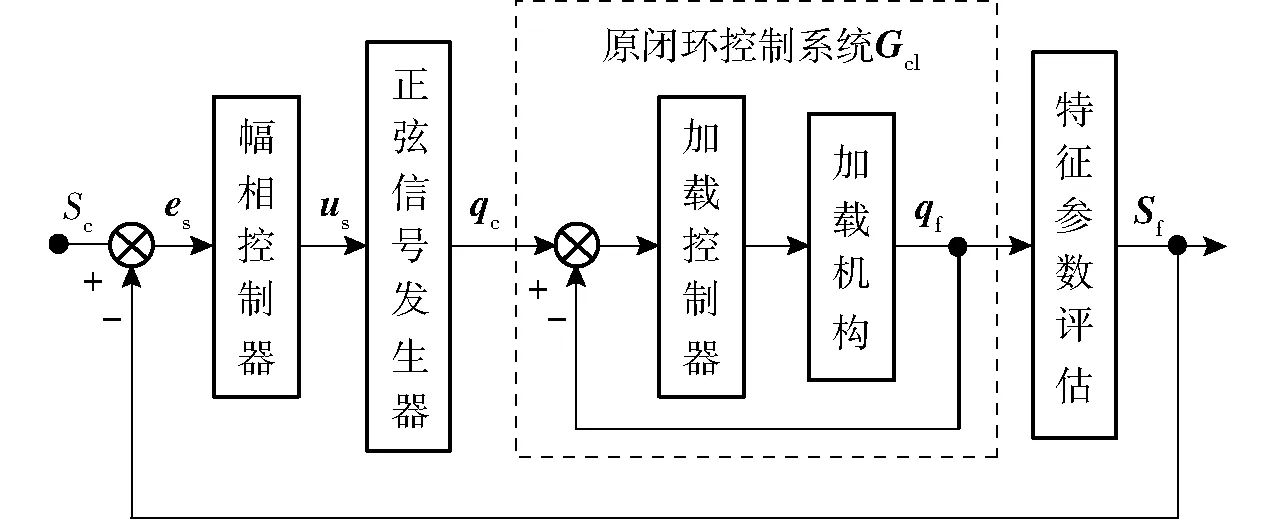
图1 改进幅相控制结构Fig.1 Improved amplitude and phase control (IAPC)

图中控制给定Sc包含期望正弦信号的幅值、相位和均值3个特征参数，Sf为从响应正弦信号qf中评估的3个特征参数。特征参数误差向量es经设计的幅相控制器产生控制量us，再经正弦信号发生器生成正弦信号控制指令qc输入到原闭环控制系统Gcl进行控制。从图1可以看出，原闭环控制系统给定的是由特征参数耦合而成的正弦信号，故原闭环控制器无法对具体每个特征参数对应通道实现单独控制参数设计，难以同时实现期望的幅值、相位及均值的精确跟踪。改进的幅相控制在原闭环控制回路外引入特征参数闭环控制回路，从而实现对组成正弦信号的各特征参数通道的解耦控制。

2 特征参数评估

2.1 幅值和均值参数评估

设给定正弦信号yc的频率、幅值、相位和均值分别为ωc、Ac、Φc、Bc，则该正弦信号可表示为

yc=Acsin(ωct+Φc)+Bc

(1)

设响应信号yf的幅值、相位、均值分别为Af、Φf、Bf，则响应输出yf可表示为

yf=Afsin(ωct+Φf)+Bf

(2)

响应信号通过一低通滤波器可实现对均值的评估。设低通滤波器为具有时间常数τ的一阶形式，则评估的均值Bef可表示为

(3)

式中s——拉普拉斯算子

相应滤除均值后的响应信号yff为

(4)

根据三角等式关系有

(5)

可见此时式(5)右边包含了一个与响应信号幅值信息有关的常量和一个两倍频的余弦分量，将其再次经过低通滤波器获得评估的幅值Aef可表示为

(6)

由于幅值和均值的评估均需要通过一低通滤波器，为获得较为精确的评估，可将低通滤波器的转折频率ωr设为：1/τ=ωr≪ωc。然而转折频率过小，会使评估速度变慢，因此转折频率的选择需要折中考虑。

2.2 相位参数评估

相位的评估可根据给定和响应正弦信号的相位差来确定。为了评估方便，首先将给定和响应信号经过同一低通滤波器，滤除其中均值部分。滤除均值后可通过检测两个信号的同向零穿越时间差来评估两者的相位差。由于均值滤除有过渡过程，在此过程中检测出来的相位差远大于360°，故在此过渡过程不对相位进行控制。为加速对相位的跟踪，相位评估分两部分：超前评估和滞后评估。超前评估以响应信号零穿越时刻开始计时，给定信号同向零穿越时刻结束，滞后评估则是相反的过程。选取两者评估出来的相位差值中较小的一个作为最终评估的相位差，则评估的相位差落在[-π, π]之间。若同选取正向零穿越，评估的相位差ΔΦ可表示为

(7)

则评估的响应正弦信号相位Φef为

Φef=Φc+ΔΦ

(8)

3 幅相控制器设计及参数整定方法

3.1 幅相控制器设计

由图1可以看出，幅相控制是外部控制回路，原闭环控制系统位于内环。通常要求内环控制器设计需保证系统具有足够的稳定裕度和一定的快速响应特性。由于包含内外环的整个控制系统开环传递函数不包含零的极点，系统为0型系统。为获得精确的正弦跟踪,控制器需增加积分环节，使系统校正为Ⅰ型。此外仅积分作用下，内环给定信号是从0开始，系统响应慢，为加快幅相跟踪速度可增加前馈环节，设计的幅相控制器如图2所示。

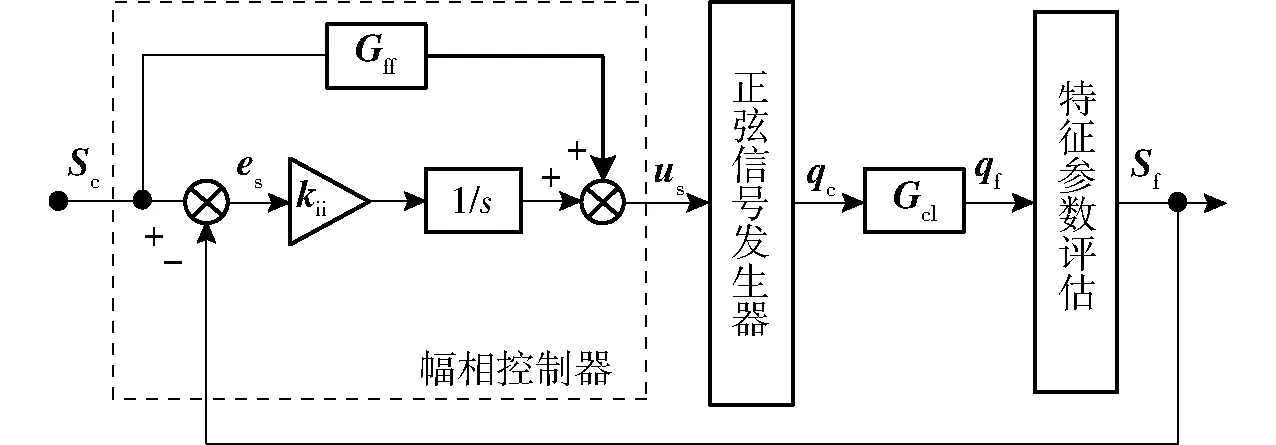
图2 幅相控制器设计Fig.2 Design of amplitude and phase controller

控制量us可表示为

(9)

式中kii——积分增益

Gff——前馈环节

3.2 控制器参数整定方法

无论采用何种幅相控制方法，为实现幅值、相位及均值的精确跟踪而设计的有关参数变量在取值方面都应考虑到响应的快速性和控制的稳定性问题。由于实际系统具有复杂的非线性时变特性，为方便分析，将图2中幅相控制的对象，即从us到Sf的传递函数Gp(s)简化表示为

(10)

式中G1(s)——从us到系统响应信号各特征参数实际值间的传递函数

G2(s)——从系统响应信号各特征参数实际值到评估值间的传递函数

τ1、τ2——G1(s)、G2(s)的时间常数，rad-1

k1(ωc)——G1(s)的增益系数，与给定信号特征参数ωc有关

引入式(9)所示幅相控制器后，从Sc到Sf的闭环传递函数G(s)可表示为

(11)

其中

GI(s)=kii/s

从式(11)可以看出，引入的前馈环节用来提高系统响应的快速性，不改变系统闭环传递函数的极点，因此对稳定性并不产生影响。若期望保留内部原闭环控制系统的初始跟踪特性，可取幅值、相位及均值的前馈环节均为常值比例系数1。由此影响到改进幅相控制稳定性的参数仅剩下积分增益项，根据劳斯稳定判据，系统稳定性条件表示为

(12)

对于内部闭环控制系统来说，均值误差即为原系统的静态误差，和跟踪正弦信号频率无关，则与给定信号频率ωc有关的幅值和相位的增益系数k1一般有以下规律：

(1)跟踪信号频率越高，内部闭环控制系统响应信号幅值衰减和相位滞后越大，k1越小，外环幅值和相位跟踪速度越慢，稳定性越好。

(2)跟踪信号频率越低，由于内部闭环控制系统响应而产生的外环幅值和相位控制通道的等效增益系数k1越大，幅值和相位跟踪速度越快，稳定性越差。

然而对于内部闭环控制系统响应信号的相位误差在相应的参数评估中已将其限制在[-π, π]以内，不会呈现如幅值误差随频率持续加大的趋势。因此为兼顾到响应的快速性和控制的稳定性，对幅值、相位及均值三者的积分增益取值时可参考以下原则：

(1)若跟踪信号频率在内部闭环控制系统频宽内，三者的积分增益可以均选取在要求跟踪的起始频率点对应的正弦信号输入下的调定值。

(2)若跟踪信号频率在内部闭环控制系统频宽外，相位和均值的积分增益取值保持先前值不变，幅值积分增益取值需随着跟踪信号频率的增加而适当增加。

4 改进幅相控制的实验结果

4.1 6自由度液压驱动冗余并联加载机构

实验平台如图3所示，为一冗余驱动并联加载机构，具有6自由度位置/力加载能力。该机构由8条对称液压缸驱动，水平方向和垂直方向各4条，相互呈正交布置。液压缸上下两端球铰分别与加载平台和基础相连。每条液压缸均配有压力传感器和位移传感器。加载试件为低阻尼圆柱形橡胶支座，被固定在加载平台与支撑柱之间。加载平台尺寸为1.5 m×1.2 m，各方向液压缸间距均为1 m，水平双向最大工作位移±50 mm，最大载荷±4 t，垂向工作最大位移±30 mm，最大载荷±8 t。下位机使用研华工控机，伺服控制程序采用xPC Target快速原型控制技术开发。

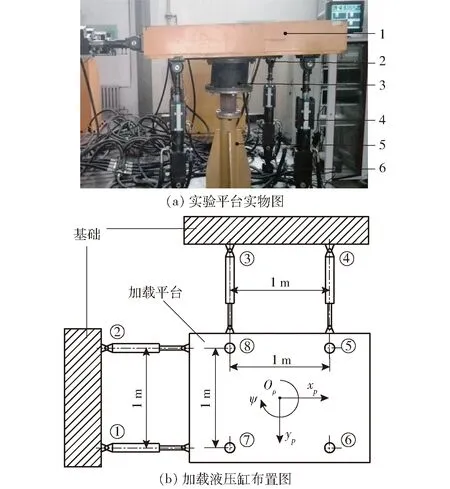
图3 实验平台Fig.3 Experimental platform1.加载平台 2.上铰 3.橡胶支座 4.液压缸 5.支撑柱 6.下铰

如图4所示，一种基于位置的位置/力混合加载控制策略被用来对试件进行多自由度位置/力混合加载[18]。通过引入选择对角矩阵S来确定各个自由度是位置控制还是力控制。在力控制方向上使用基于位置的显力控制，经力控制器输出的是力控制方向上的平衡位置，将其与位置控制方向上的指令信号合并作为总的位置指令，输入到内部位置闭环控制回路进行跟踪。自由度反馈位置由采集的缸位移经运动学正解解算获得，自由度反馈力由采集的缸两腔压力经力雅可比矩阵转换得到。内部位置闭环控制包括位置跟踪和内力抑制两部分。位置控制器采用比例-积分-滞后形式，内力控制器采用比例-积分形式，力控制器采用比例-积分和双滞后校正环节。

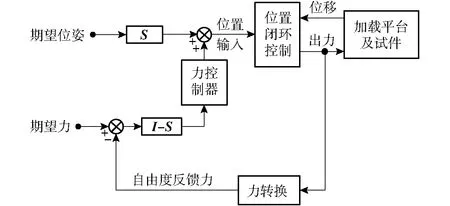
图4 基于位置的位置/力混合加载控制策略Fig.4 Position-based hybrid position/force loading control

位置/力混合加载时设定z自由度方向为力控制，其他自由度方向均为位置控制。经上述控制器校正后在小幅值随机信号激励下辨识x自由度位置和z自由度力的闭环频率响应特性，分别如图5和图6所示。

图5 x自由度位置闭环频率响应特性Fig.5 Position close-loop frequency response characteristics in x degrees of freedom (DOF)

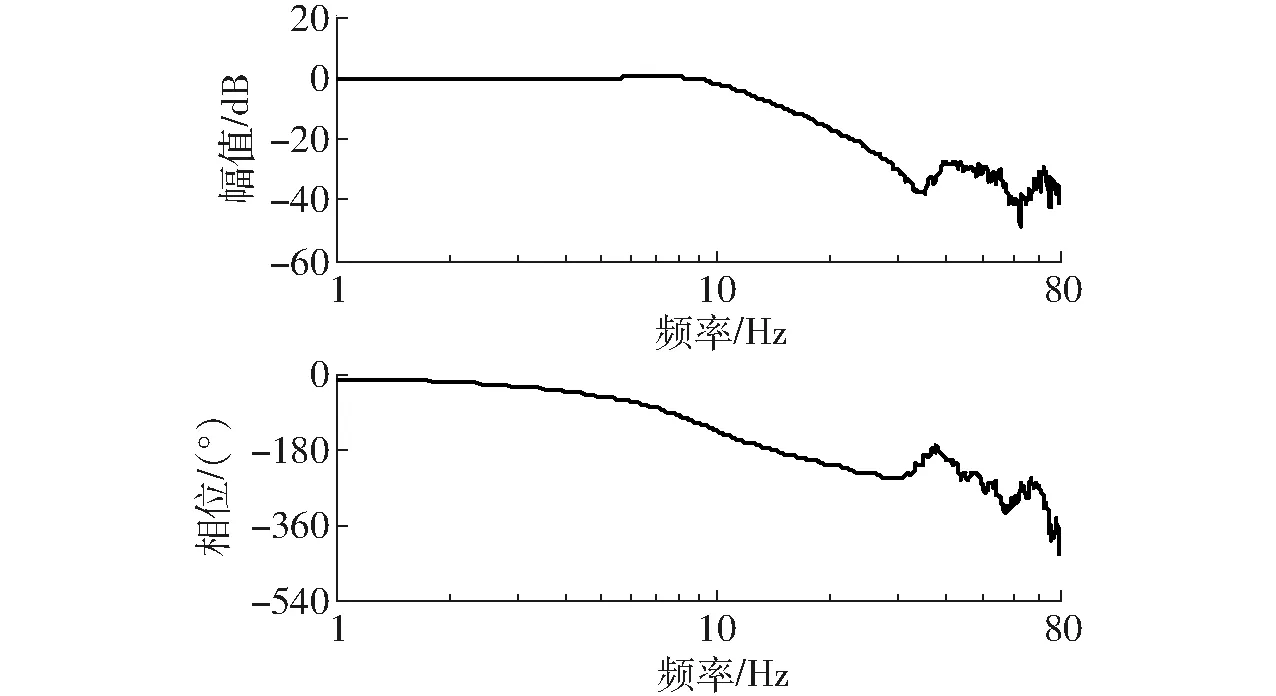
图6 z自由度力闭环频率响应特性Fig.6 Force close-loop frequency response characteristics in z DOF

在位置控制方向，由于液压系统小阻尼特性造成位置开环频率特性幅值裕量较小，弹性试件的耦合作用进一步降低系统的阻尼比和开环穿越频率[19-20]，x自由度位置闭环系统在8 Hz时幅值衰减3 dB，相位滞后94°。在力控制方向，力控制性能严重受到试件特性的影响，在试件固有频率(约34 Hz)附近处出现一个较深的反谐振峰，此处对应的力加载性能较差，z自由度力闭环系统在11 Hz时幅值衰减3 dB，相位滞后150°。由此可见，加载机构受到试件的耦合作用影响，其位置和力的闭环频宽均较低，且相位滞后严重。

4.2 正弦位置/力加载实验

首先分析在提出的改进幅相控制下正弦位置信号跟踪性能。给定x自由度方向正弦位置信号为5sin(4πt+π/4)-2，其他自由度位置控制指令均为零。幅相控制器参数中幅值、相位、均值的前馈增益分别取0.5、0.5和0，积分增益分别取0.3、1和0.4。在3.7 s时刻开始启用幅相控制，之前使用原内部位置控制器控制。由图7a、7b可见，无幅相控制下跟踪误差幅值约为1.8 mm，幅相控制下跟踪误差迅速减小，最大跟踪误差最终不超过±0.1 mm，降低了约94%。图7c～7e显示了对响应信号的特征参数评估情况，可以看出特征参数评估速度快且精度高，其中幅值和均值的评估受低通滤波的影响，评估结果有与响应信号同频率的正弦小幅值干扰。从图7f输出控制量来看，此干扰经过积分作用的衰减并不会使控制量产生较大的波动，控制曲线整体比较平稳。

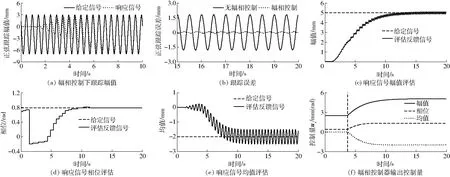
图7 x向2 Hz正弦位置跟踪Fig.7 Sinusoidal position tracking at 2 Hz in x DOF

进一步分析提出的改进幅相控制对超出系统频宽外的高频正弦位置/力的跟踪效果。分别给定x自由度方向幅值0.1 mm、频率20 Hz的正弦位置信号和z自由度方向幅值0.5 t、频率30 Hz、均值3 t的正弦力信号。如图8a所示，当给定正弦位置信号频率接近x自由度位置开环频率特性中谐振峰对应频率点位置(约25 Hz)时，由于系统非线性因素的存在造成正弦位置跟踪波形失真较大，降低了幅相控制下位置跟踪精度。但从实验结果可以看出，幅相控制的正弦跟踪误差幅值比无幅相控制仍降低70%以上。同样如图8b所示，当给定正弦力信号频率接近z自由度力开环频率特性中反谐振峰对应频率点位置(约34 Hz)时，力跟踪波形失真较大，幅相控制下力跟踪误差也加大。受到试件特性影响，该频率点处无幅相控制时系统几乎不响应，而采用幅相控制后力跟踪误差最终落在±0.12 t以内，比无幅相控制误差幅值降低了76%。

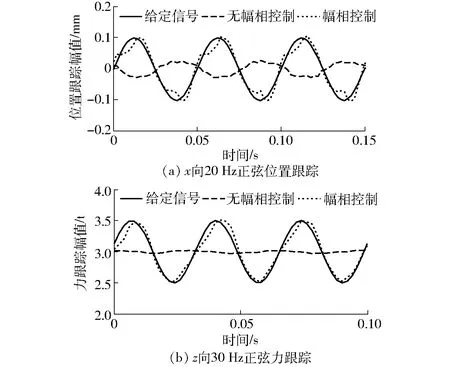
图8 高频正弦位置/力跟踪Fig.8 High-frequency sinusoidal position/force tracking

4.3 正弦位置/力混合加载实验

在对橡胶支座试件进行水平位置/垂向力混合加载时，由于橡胶支座自身内部复杂特性，垂向力加载精度常常会严重受到水平方向的运动干扰影响[5]。分析橡胶支座试件进行位置/力混合加载时在提出的幅相控制下正弦位置/力信号跟踪性能。给定z方向幅值1 t、频率1 Hz、均值3 t的正弦力信号，在37 s时继续给定x自由度方向幅值20 mm、频率0.5 Hz的正弦位置剪切指令，其他自由度位置指令均给零。由图9可以看出，在未进行水平剪切前，力跟踪很快收敛到±0.02 t以内。当水平剪切开始时，由于此时橡胶支座垂向刚度特性的改变，力跟踪误差稍有加大，但依然保持在较小的范围内。最终在改进幅相控制下正弦力跟踪误差不超过给定幅值的±3%，正弦位置跟踪误差不超过给定幅值的±2%，显示了改进幅相控制良好的正弦位置/力跟踪性能。

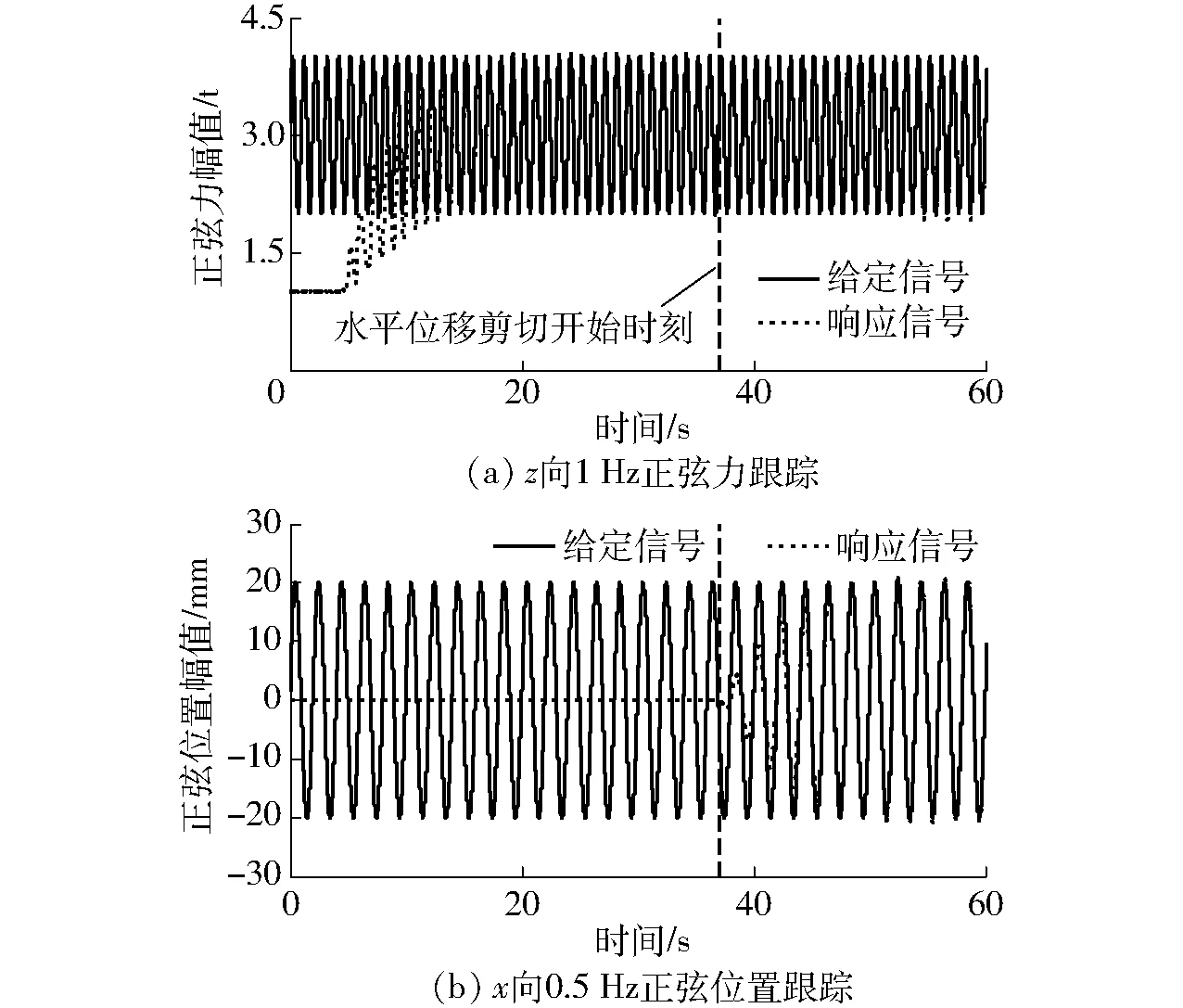
图9 正弦位置/力混合加载实验结果Fig.9 Hybrid sinusoidal position/force loading experimental results

5 结论

(1)提出了一种改进幅相控制方法，通过对正弦信号幅值、相位、均值3个特征参数的评估，在原闭环控制系统外引入特征参数闭环控制回路，实现了对组成正弦信号的各特征参数通道的解耦控制。

(2)设计了幅相控制器，给出了控制器参数整定方法，保证了控制系统的稳定和快速响应。

(3)并联加载机构正弦位置/力加载实验结果表明，改进的幅相控制能有效提高正弦位置/力信号的跟踪精度，该方法具有控制结构简单、调节参数少、参数整定方便的特点。