PID神经网络算法对K型热电偶非线性校正

苏淑靖 吕楠楠 翟成瑞

摘 要： 针对火箭发射场发射效应测温系统中K型热电偶存在的非线性特性，设计中将非线性特殊点作为训练样本，采用新型动态PID神经网络算法对热电偶进行非线性校正。针对基本BP算法收敛慢、易陷入局部极值的缺点，提出利用粒子群算法来改进网络的寻优过程，并在传统算法基础上对其惯性权值的递减式子进行改进。使用Matlab建模仿真表明，改进算法在寻优过程中，收敛速度快，全局寻优能力强，有较好的控制效果。拟合出的温度电压关系呈现好的线性度，相对误差均控制在1%以内，提高了系统测试精度，满足对火箭发射时温度环境效应的监测要求。

关键词： PID神经网算法； K型热电偶； 粒子群优化； 非线性校正； 惯性权值； Matlab

中图分类号： TN711?34； TH811； TP206+.1 文献标识码： A 文章编号： 1004?373X（2018）14?0074?05

Nonlinear correction of K?type thermocouple using PID neural network algorithm

SU Shujing， L? Nannan， ZHAI Chengrui

（Key Laboratory of Electronic Measurement Technology， North University of China， Taiyuan 030051， China）

Abstract： In allusion to the nonlinear feature of K?type thermocouple in the launch effect temperature measurement system of the rocket launching site， the nonlinear special points are taken as the training samples in the design， and a new dynamic PID neural network algorithm is adopted to perform the nonlinear correction of the thermocouple. In allusion to the disadvantages of slow convergence and easy to be trapped in the local extremum of the basic BP algorithm， the particle swarm algorithm is proposed to improve the network optimization process， and its inertia weight decreasing formula is improved on the basis of the traditional algorithm. The Matlab modeling simulation shows that the improved algorithm has a fast convergence speed， a strong global optimization capability， and a good control effect during the optimization process； the fitted temperature?voltage relationship presents a good linearity； the relative errors are all controlled within 1%； the improved algorithm can improve the test accuracy of the system， and meet the monitoring requirement of temperature environment effect during rocket launch.

Keywords： PID neural network algorithm； K?type thermocouple； particle swarm optimization； nonlinear correction； inertia weight； Matlab

0 引 言

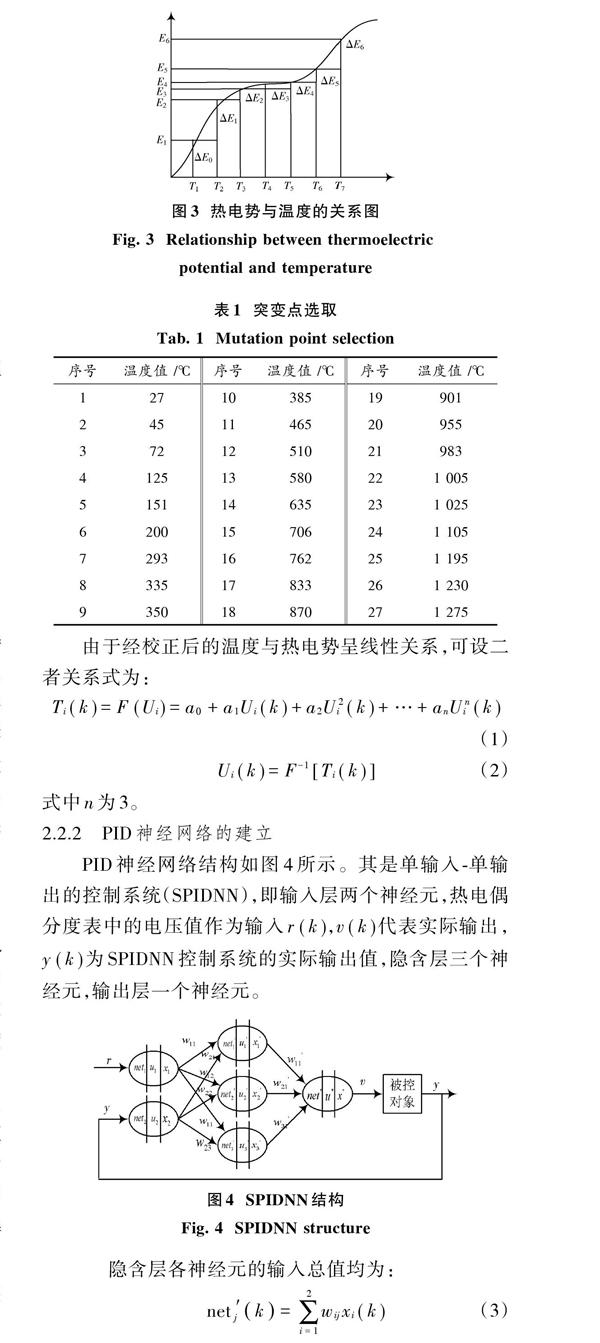
热电偶自身的物理特性致使其输出的热电势[E]与温度[t]之间存在非线性关系，针对目前测试系统的宽范围、高精度测量需求，需要减少非线性测量误差。K型热电偶的非线性校正方法有查表法、多项式拟合法、PID神经网络法[1]。其中，查表法使用大量数据，极易受到存储容量的限制；最小二乘法以[T=d0+d1E+d2E2+…+dnEn]形式拟合，在高温阶段误差较大[2]。针对以上问题，本设计采用基于粒子群算法的PID神经网络算法对K型热电偶进行非线性校正，同时系统具有PID控制的快速输入/输出动态特性。

1 测温系统分析及校正原理

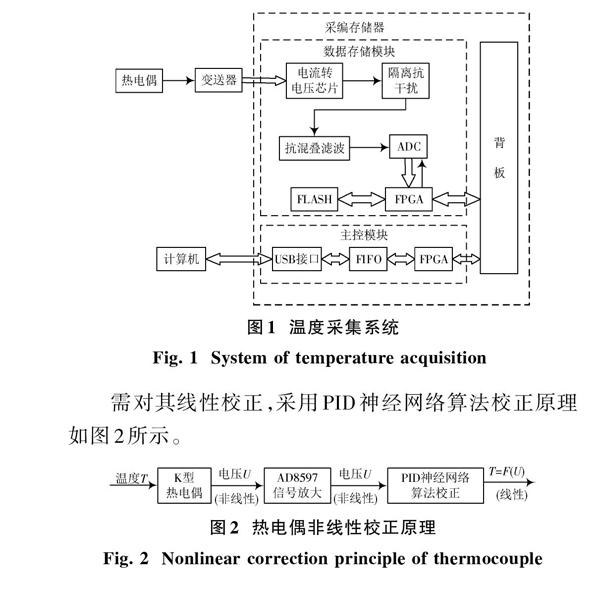
如图1所示，温度采集系统包括K型热电偶、变送器、采编器及测控计算机。在温度采集系统中，针对ADC误差、传输线路误差、调理和输入跟随误差，设计采集存储模块，其由电流转电压模块、抗混叠滤波器、模/数转换模块、FPGA控制模块，FLASH模块组成；经变送器将电压信号转换成幅度为4～20 mA的电流信号进行传输，抵抗恶劣环境干扰。而对于传感器误差，在实际应用中即使经过冷端补偿，热电偶测温时冷端也很难保持为0 ℃。

2 基于粒子群算法的PID神经网络非线性校正

2.1 PID神经网络理论

传统神经网络中神经元仅具有静态的输入/输出特性，若用它构成控制系统时必须附加其他动态部件[3]。PIDNN以PID控制器的形式定义网络隐含层，其隐含层包括比例元、积分元和微分元三个神经元，采用粒子群算法调整权重值，反复进行学习和训练，使目标函数达到最优[4]。根据网络输出值的不同，PIDNN分为单输出PIDNN（SPIDNN）和多输出PIDNN（MPIDNN）[5]，本文采取单输出方式。

2.2 温度控制系统建模

2.2.1 訓练样本数据获取

在实际运用中，本设计中所要测量温度范围是0～1 300 ℃，所以在选择训练样本时选取热电偶分度表中的特殊点，避免数据量过大造成浪费，同时节省了计算时间。图3为典型的热电特性曲线图，横坐标表示温度[T]，纵坐标表示热电势[E]。

图3中二者明显呈现出非线性关系。选取特殊点时，首先对[T]等间距取值，通过分析[E]变化情况即[ΔE]值便可找到特殊点。令[ΔZi=ΔEi-ΔEi-1]，取正数[α]作为门限值，当[ΔZi<α]时将该点领域内近似为线性，当[ΔZi≥α]时则可判断该点发生突变，即[（Ti，Ei）]作为特殊点。

表1为温度在0～1 300 ℃范围内选取的突变点，突变点对应的K型热电偶分度表数据作为训练样本。

由于经校正后的温度与热电势呈线性关系，可设二者关系式为：

[Ti（k）=F（Ui）=a0+a1Ui（k）+a2U2i（k）+…+anUni（k）] （1）

[Ui（k）=F-1[Ti（k）]] （2）

式中n为3。

2.2.2 PID神经网络的建立

PID神经网络结构如图4所示。其是单输入?单输出的控制系统（SPIDNN），即输入层两个神经元，热电偶分度表中的电压值作为输入[r（k）]，[v（k）]代表实际输出，[y（k）]为SPIDNN控制系统的实际输出值，隐含层三个神经元，输出层一个神经元。

隐含层各神经元的输入总值均为：

[net′jk=i=12wijxi（k）] （3）

式中：[j=1，2，3]；[wij]为输入层到隐含层的连接权重值。针对积分环节出现的积分饱和现象、微分信号引入过程中易引进高频干扰的问题，采取变速积分和不完全微分的PID控制策略。在改进积分元中设置系数[f[e（k）]]，积分神经元输出表示如下：

[x′2（k）=1，x′2（k）>1x′2（k-1）+f[e（k）]u′2，-1≤x′2（k）≤1-1，x′2（k）<-1] （4）

式中：

[f[e（k）]=1，e（k）≤BA-e（k）+BA，BA+B] （5）

[e（k）]是神经网络实际输出与理想输出的均方差值；[A]，[B]均为常数。当[e（k）]增大时，[f（k）]减小；[e（k）]减小时，[f（k）]增大。将当前输入值加权后的和作为神经元输出值。在改进微分元中加入了输出自反馈的加权和，其表示如下：

[x′3（k）=1，x′3（k）>1（1-T）[u′3（k）-u′3（k-1）]+Tx′3（k-1），-1≤x′3（k）≤1-1，x′3（k）<-1] （6）

式中，[0≤T≤1]。

2.2.3 粒子群优化神经网络算法

使用改进的PSO算法优化权值，首先初始化所有子群粒子的速度、位置及每一子群的最优位置，性能指标函数作为适应度函数计算每个粒子的适应度值[g（k）]。性能指标函数为：

[e（k）=1mk=1mr（k）-y（k）2 =1mk=1mUi（k）-F-1[Ti（k）]2] （7）

式中：[e（k）]是神经网络实际输出与理想输出的均方差值；[m]为样本数目。

然后将每个粒子的适应度与个体极值及全局极值进行比较，确定新的个体极值[Pi]与全局极值[Pg]。按照式（8）和式（9）更新速度与位置。将个体极值进化停滞步数与预设值进行比较，按照式（8）不断更新速度，比较全局极值进化停滞步数与预设值，按照式（9）不断更新位置。

式中：[Vi（k）]是粒子[i]的速度；[w]为惯性权重，随迭代次数线性递减，保证收敛；[Xi（k）]为粒子所在位置；[r1]，[r2]，[r3]，[r4]是（0，1）之间的随机数；[c1]，[c2]为学习因子；[Ti]为粒子[i]个体极值进化停滞步数；[Tg]为全局极值进化停滞步数，[T]为预设值。在惯性权值的变化过程中，本设计中采取非线性权值递减方法，表达式如下：

[w=[0.26+e（-ρ*t/tmax-0.9）]*wmax] （10）

式中：[wmax]为所取最大权值；[t]为当前迭代次数；[tmax]为迭代总次数；[ρ]为正数，根据惯性权重的范围本文选取4.5。粒子按照式（11）更新自身位置：

[Xi（k+1）=Xi（k）+Vi（k+1）] （11）

若未达到停止迭代的条件则继续返回计算适应度值；若性能指标函数[e（k）]值达到期望值或者到达预设的迭代次数时，得到最优粒子，将极值赋给权值，计算结束。

2.2.4 仿真结果分析

初始化位置矢量[X]为[-0.1，0.1]的随机数，速度矢量[V]为[-0.3，0.3]的随机数；取学习因子[c1=1]，[c2=1]；惯性权重[w]的取值范围是[0.25≤w≤0.95]；选择种群粒子数为27；迭代次数为40。Matlab仿真结果如图5所示。

图5是在粒子群算法进化过程中，全局最优值的适应度随PSO迭代的变化过程。可看出适应度函数在寻优过程中在第5次迭代处基本趋于0，即网络实际输出与理论输出的均方差逐渐趋于0，训练后的数据较为快速地趋于标准数据，二者间误差较小。该过程中收敛明显，收敛速度快且收敛性好。

惯性权重的选取对算法的收敛速度是很重要的。图6中针对粒子群算法中的惯性权重，将传统算法与改进算法进行仿真对比。从图6中可看出，传统粒子群算法过程中，惯性权值呈线性递减，由于粒子在向群内最优位置运行时速度较快，在其到达最优点处时极有可能因为速度太快而错过；所以在设计中使用改进的惯性权值算法，将惯性权重按照指数的形式逐渐降低，粒子的运行速度随着粒子与最优点间距离的减小有较为明显的降低，保证了在寻优前期有快速收敛的能力，也确保后期有较好的收敛效果。

图7与图8分别是传统PSO算法寻优过程和改进PSO算法寻优过程。两图比较，二者均可在迭代次数较小处获得最优解，惯性权值未优化时，极易陷入局部最优。使用惯性权值优化算法时，可经过更少的迭代次数获得最优值，易跳出局部最优点，且其在前期有较好的收敛速度；在增强粒子局部寻优能力的同时，保证了算法的收敛性，寻优效果明显，运行效率高；具有更强的全局搜索能力。同时优化算法的精度明显高于传统算法，提高了传感器测量的可靠性和准确性。采用改进PSO算法对PID神经网络进行仿真，解方程组得系统校正方程最优解：[a0=0.171 0]，[a1=21.678 0]，[a2=0.026 0]，[a3=-0.000 8]。在输入温度值一定的条件下，经神经网络训练后部分电压值与标准电压值对比结果如表2所示，可以直观地看出误差最小的可以达到0.1%，最大误差控制在1%内。训练效果明显得到改善。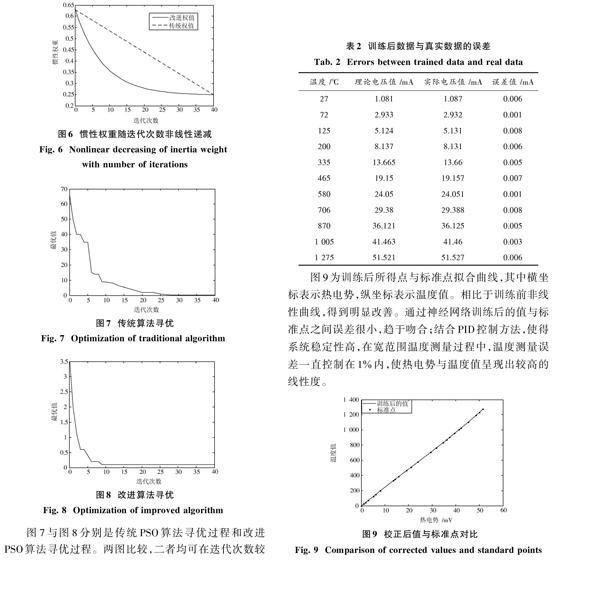

图9为训练后所得点与标准点拟合曲线，其中横坐标表示热电势，纵坐标表示温度值。相比于训练前非线性曲线，得到明显改善。通过神经网络训练后的值与标准点之间误差很小，趋于吻合；结合PID控制方法，使得系统稳定性高，在宽范围温度测量过程中，温度测量误差一直控制在1%内，使热电势与温度值呈现出较高的线性度。

3 结 论

在宽范围高精度测温系统中，针对K型热电偶输出的热电势[E]与温度[t]之间的非线性关系，建立PID神经网络对其进行非线性校正，采用粒子群算法进行寻优取值。选取[E]?[t]曲线中特殊拐点的标准值作为训练样本，对寻优过程中的惯性权值改进，增强其全局寻优能力。仿真结果表明：控制系统稳定性较高，精确性提高；训练所得温度值与标准值之间误差均在1%以内，且二者拟合效果好，收敛速度快。精确温度信号获取为火箭发射塔架的健康评估提供可靠依据。

参考文献

[1] 段艳明.基于PSO算法和BP神经网络的PID控制研究[J].计算机技术与发展，2014，24（8）：238?241.

DUAN Yanming. Reserch of PID control based on BP neural network and PSO algorithm [J]. Computer technology and development， 2014， 24（8）： 238?241.

[2] 朴海国，王志新.基于CPSO的PID神经网络及偏航电机控制策略[J].电机与控制学报，2010，14（9）：55?62.

PIAO Haiguo， WANG Zhixin. Control strategy of CPSO?based PID neural network and a yaw motor [J]. Electric machines and control， 2010， 14（9）： 55?62.

[3] GAO M Y， CHEN S X， CHENG L L， et al. Online measurement of battery internal resistance based on AC impedance method [J]. Advanced materials research， 2013， 718?720： 773?778.

[4] 屈毅，宁铎，赖展翅，等.温室温度控制系统的神经网络PID控制[J].农业工程学报，2011，27（2）：307?311.

QU Yi， NING Duo， LAI Zhanchi， et al. Neural networks based on PID control for greenhouse temperature [J]. Transactions of the Chinese Society of Agricultural Engineering， 2011， 27（2）： 307?311.

[5] 于立君，陈佳，刘繁明，等.改进粒子群算法的PID神经网络解耦控制[J].智能系统学报，2015，10（5）：699?704.

YU Lijun， CHEN Jia， LIU Fanming， et al. An improved particle swarm optimization for PID neural network decoupling control [J]. CAAI transactions on intelligent systems， 2015， 10（5）： 699?704.

[6] MOHANDES M A. Modeling global solar radiation using particle swarm optimization [J]. Solar energy， 2012， 86（11）： 3137?3145.

[7] 沈锡.基于粒子群优化算法的船舶航向PID控制[D].大连：大连海事大学，2011.

SHEN Xi. Ship course PID control based on particle swarm optimization [D]. Dalian： Dalian Maritime University， 2011.

[8] 周西峰，林莹莹，郭前岗.基于粒子群算法的PID神经网络解耦控制[J].计算机技术与发展，2013，23（9）：158?161.

ZHOU Xifeng， LIN Yingying， GUO Qiangang. PID neural network decoupling control based on particle swarm optimization [J]. Computer technology and development， 2013， 23（9）： 158?161.

[9] 应进.基于粒子群算法的航空发动机多变量控制研究[D].南昌：南昌航空大学，2011.

YING Jin. Research on multi?variable control of aero engine based on particle swarm optimization [D]. Nanchang： Nanchang Hangkong University， 2011.

[10] 俞凯耀，席东民.人工鱼群算法优化的PID神经网络解耦控制[J].计算机仿真，2014，31（10）：350?353.

YU Kaiyao， Xi Dongmin. Optimized PID neural network decoupling control based on artificial fish optimization [J]. Computer simulation， 2014， 31（10）： 350?353.